Kenguroppgaver – da snakker vi!

Mange kenguruoppgaver har problemstillinger som egner seg godt for pararbeid og diskusjon rundt løsninger og løsningsstrategier. Når elever er uenige om løsninger og må argumentere for sine løsningsvalg, er diskusjonene mellom elevene i gang. Dette gir ofte et godt utgangspunkt for å kunne arbeide med og forstå et matematisk problem. Matematisk argumentasjon er trukket fram som en viktig egenskap i ny læreplan, spesielt i kjerneelementene Resonnering og argumentasjon og Representasjon og kommunikasjon.
Jeg vil her vise eksempel på to oppgaver jeg har brukt i en 7. klasse. Begge syns jeg egner seg godt til å stille oppfølgingsspørsmål som kan sette i gang gode matematiske diskusjoner.
Dersom du er bevisst på valg av organiseringsform, kan også det forsterke læringsutbyttet. I begge disse oppgavene lot jeg elevene begynne med pararbeid for så å gå i grupper på fire, før vi oppsummerte i fellesskap.
Her er den første oppgaven jeg brukte:
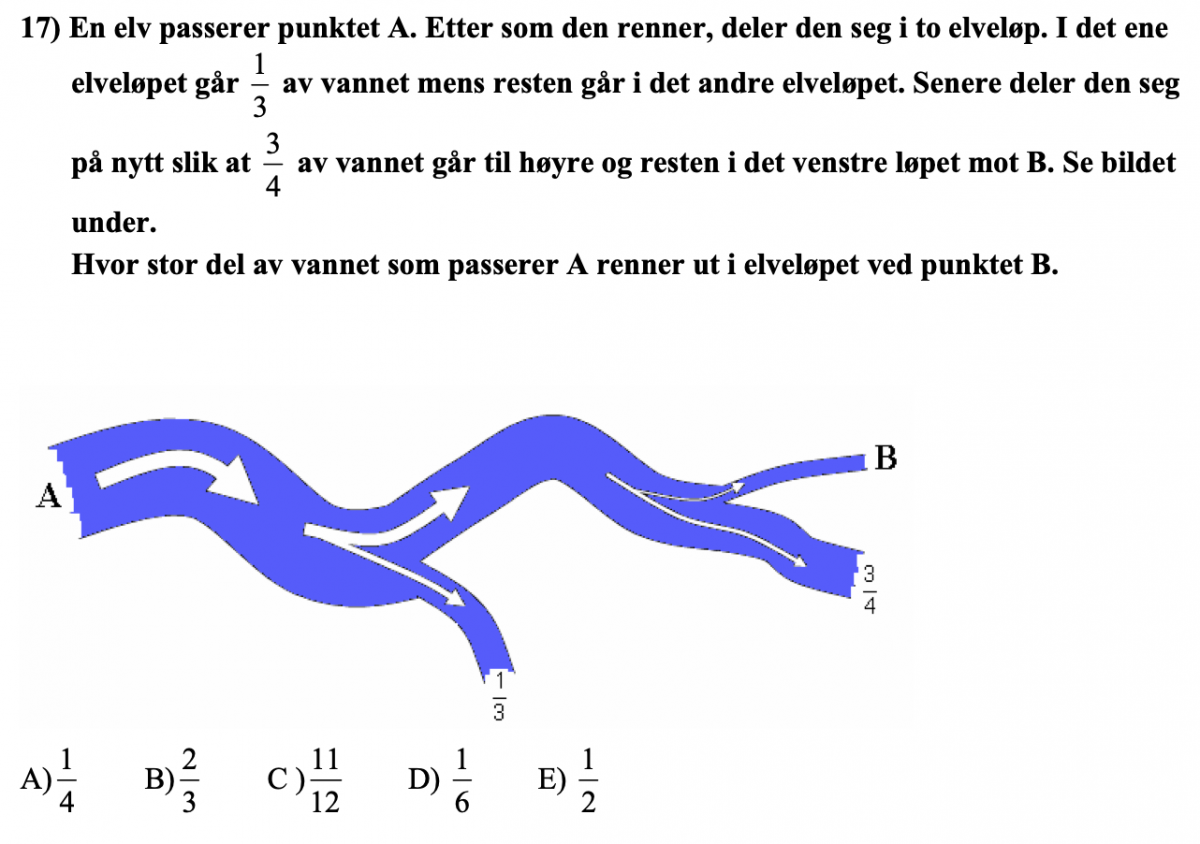
Elevene fikk følgende utfordringer fra meg:
- Kan dere finne ett eller flere svaralternativer som umulig kan være riktig. Her må dere selvsagt kunne argumentere for hvorfor alternativet ikke kan være riktig.
- Kan dere velge andre tall i oppgaven, men slik at svaralternativet fortsatt er det samme?
- Kan dere velge andre tall i oppgaven slik at et av de andre svaralternativene blir riktig?
Her er den andre oppgaven:

Elevene fikk følgende utfordringer:
- Bruk gjerne kort og vis hvordan du kommer fram til løsningen.
Forklar hvorfor dette må bli riktig. - Lag en lignende oppgave til et annet par der du bruker et annet antall kort og lager minst tre løsningsalternativer der bare ett skal være riktig.
Hvorfor bruker jeg kenguruoppgaver?
Kenguruoppgavene egner seg godt til å utvide slik at de skaper utgangspunkt for en matematisk diskusjon. Oppgaver der elevene er avhengig av å snakke sammen, diskutere og bli enige om løsninger anbefales både fordi det er motiverende og fordi det kan gi en bredere forståelse. Ved en oppsummering i fellesskap, må elevene kunne argumentere for sine løsninger. Her finner du flere eksempler.
Denne artikkelen stod også på trykk i Tangenten nr. 01/21
