Fordeling av sjokoladekaker

Brøk som kvotient. Problemløsing. Resonnering.

Dette opplegget er utarbeidet som en del av prosjektet Mestre Ambisiøs Matematikkundervisning (MAM).

Materiell til å skrive på undervegs og til plakat (A3-ark, flippoverark, tavler e.l.).

Tusjer eller andre skrivesaker (og eventuelt tape).

Konkretiseringsmateriell.

Til lærer

Oppgaveark Fordeling av sjokoladekaker (PDF)

Kort undervisningsnotat problemløsing (PDF)

Presenter oppgaven muntlig for elevene. Elevene skal finne ut hvem som får mest sjokoladekake, og hvor mye mer, når tre gutter skal dele ei sjokoladekake likt mellom seg, mens åtte jenter skal dele tre sjokoladekaker likt mellom seg. Elevene arbeider i grupper på tre og fire, og gruppene skal presentere løsningene skriftlig (plakater) og argumentere for at løsningen deres er korrekt. Observer på hvilken måte elevene samarbeider og hvordan hver enkelt bidrar i gruppearbeidet. Vær bevisst på hvordan du som lærer bidrar underveis i arbeidet.

Fordeling av sjokoladekaker

Elevene i en klasse er på skolekjøkkenet og baker sjokoladekaker. De tre guttene i klassen baker ei sjokoladekake, og de åtte jentene i klassen baker tre sjokoladekaker. Guttene deler sjokoladekaken likt mellom seg, og jentene deler sine tre sjokoladekaker likt mellom seg. Hvem får mest, ei jente eller en gutt? Hvor mye mer?

Matematiske sammenhenger

I denne aktiviteten arbeides det med brøk som svaret på en divisjon (kvotient). Brøken er et resultat av lik deling. Brøken `(3)/(4)` forteller hvor mye kake hver person får hvis vi deler 3 kaker likt mellom 4 personer. Hver gutt får `(1)/(3)`, mens hver jente får `(3)/(8)`. Dette er ikke opplagt for elevene, spesielt hvis de tidligere kun har erfaringer med brøk som en del av en hel.

Før du møter elevene bør du tenke gjennom følgende problemstillinger slik at du er forberedt på å lede arbeidet fram mot det faglige målet.

• Bruk av konkreter? Hvordan tegne? Hvordan skrive dette med symboler?
• Hvordan er det lurt å tegne kakene? Vil ei rund eller rektangulær kake egne seg best til å dele og sammenligne?
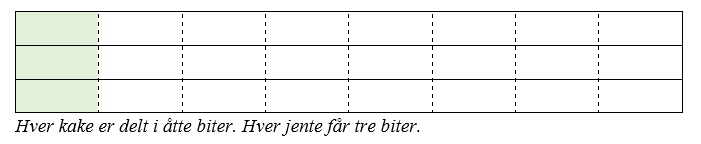
• Hvordan dele opp kakene? Hvordan ser bitene ut? (Bitene må ha like store areal, men trenger ikke være av samme form)
• Hvordan er sammenhengen mellom antall kaker og gutter og mengden kake som hver gutt får (1 kake og 3 gutter osv.)? Tilsvarende for jentene.
• Hvordan sammenligne brøker? Utfordre elevene til å forklare hvordan de kan finne ut hvem som fikk mest ved å sammenligne brøker med like tellere eller like nevnere. Hvor mye mer?
  • Undersøk likeverdige brøker og se på tellerne:
    
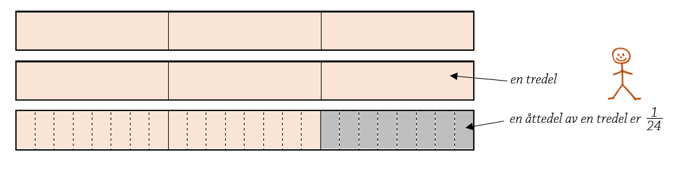
    Det er lett å sammenligne brøker med samme teller. I dette eksemplet skal`(1)/(3)` sammenlignes med `(3)/(8)`. Brøken`(1)/(3)` er likeverdig med brøken `(3)/(9)`. Når telleren er lik, er antall biter de samme, men størrelsen på bitene er forskjellige. Brøken `(3)/(8)` er større enn `(3)/(9)`, fordi åttendels-bitene er større enn en nidels-bitene ( `(1)/(8)` er større enn `(1)/(9)` ).
• Hver jente får `(1)/(8)` av en `(1)/(3)`kake mer enn hver gutt (`(1)/(8)` av den den tredelen av ei kake som er til overs). Hvor stor del av en kake er det? Hvordan uttrykke det som en brøk (del av kaken)? Behov for felles nevner? Kan en tegning være til hjelp? Konkretiseringsmateriell?

  

  `(1)/(3)` + `(1)/(3)` : 8 = `(8)/(24)` + `(1)/(24)` = `(9)/(24)` = `(3)/(8)`

• En annen måte å se det på er at jentene får `(1)/(8)`+`(1)/(8)`+`(1)/(8)` = `(3)/(8)`, og guttene får `(1)/(3)`. Deretter se på differensen mellom `(3)/(8)` og `(1)/(3)`.
• Se på sammenhengen mellom løsningsmetodene og ulike representasjoner (verbale, visuelle og symbolske).

Kritiske momenter

• Hva med tegninger/delinger som ikke viser til lik deling? Viktig at elevene forklarer ideene sine og argumenterer for løsninger. Noen elever vil kanskje si at det er lik deling bare kaken er delt i tre deler.
• Spørsmålet "hvor mye mer" vil være utfordrende for elevene. (Observer hva elevene gjør mens de jobber i grupper).

Forventede elevrespons

• Lager tegning, deler opp kakene i biter som er like store.
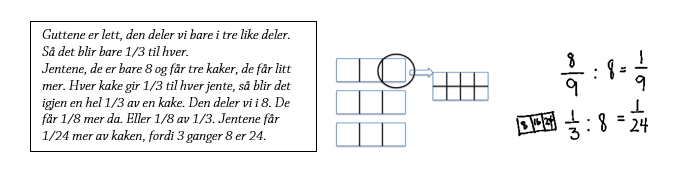
• Teller antall biter som hver elev får. Dersom kakene er delt i tre like biter, vil hver gutt få én bit. Hver jente får også én bit, men de får en bit til overs (tre kaker er ni biter). Jentene får en liten bit til, så de får to biter hver (en stor og en liten).
• Forklarer at hver gutt får `(1)/(3)` mens hver jente får `(1)/(3)`pluss 1 bit av en liten bit. Kanskje noen sier at hver jente får `(1)/(3)` pluss `(1)/(8)` av `(1)/(3)`.
• Uttrykker at hver gutt får `(1)/(3)` mens hver jente får tre `(1)/(8)`- biter, men ser ikke at de kan skrive det som `(3)/(8)`.
• Bruker proporsjonal resonnering (multiplikativ tenking). Sier for eksempel at hvis vi «jekker» opp antall jenter slik at de «får like mye som hver gutt» eller «like mange jenter på hver kake» så måtte det være 9 jenter.

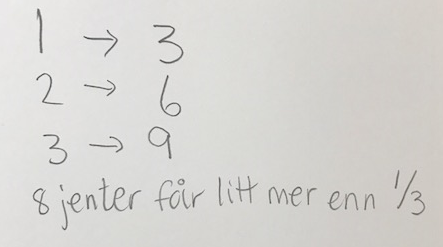
I matematiske diskusjoner med elever skal læreren prøve å fremme elevenes resonnering og forståelse knyttet til det faglige innholdet som er definert som hensikten med aktiviteten.