Fra den ene til den andre

Geometri, kongruensavbildning, rotasjon, speiling, parallellforskyving.

PC med GeoGebra.

Aktiviteten er inspirert av en workshop Rikke Teglskov og Bo Kristensen hadde på den Nordisk-baltiske GeoGebra-konferansen i 2019.



Elevene arbeider i par. Først lager begge en oppgave (uten at den andre ser det) og deretter skal de prøve å løse hverandres oppgave. Sørg for at GeoGebra ikke viser navn på nye objekter (under Innstillinger).

Oppgave til elevene

• Lag en Mangekant.
• Gjør kongruensavbildninger på mangekanten (og avbildningene).
• Skjul alle objekter bortsett fra start- og sluttfiguren.
• Skjul Algebrafeltet.

Kommentarer til læreren

Elevene kan lage oppgavene med eller uten rutenett. De kan velge hvordan figurene skal se ut og hvor mange kongruensavbildninger de ønsker å gjøre. Oppfordre elevene til å bruke farger eller mønster på start- og sluttfiguren. Det gjør det lettere når de skal snakke om figurene underveis i løsningsprosessen.



Når elevene skal løse oppgavene, kan de bruke både start- og sluttfiguren som utgangspunkt. De kan også bruke Linje, Linjestykke, Sirkel definert med sentrum og periferipunkt, Midtpunkt eller sentrum, Glider eller andre verktøy som hjelp. Det finnes alltid flere måter å løse oppgavene på, uansett hvilke kongruensavbildninger elevene som laget oppgavene har brukt. Elevene kan derfor løse samme oppgave flere ganger. Oppfordre de gjerne, når de har løst noen oppgaver, til å prøve å løse oppgavene med færrest mulige kongruensavbildninger.



La elevene samarbeide om å løse oppgavene. Eleven som har laget oppgaven skal ikke avsløre løsningen sin, men i stedet støtte eleven som ikke har laget oppgaven i løsningsprosessen og forsøke å forstå hvordan han/hun tenker. Det finnes alltid flere løsninger, og eleven som løser oppgaven vil sjelden velge akkurat samme fremgangsmåte som eleven som har laget oppgaven. Det er en nyttig erfaring for begge elevene.

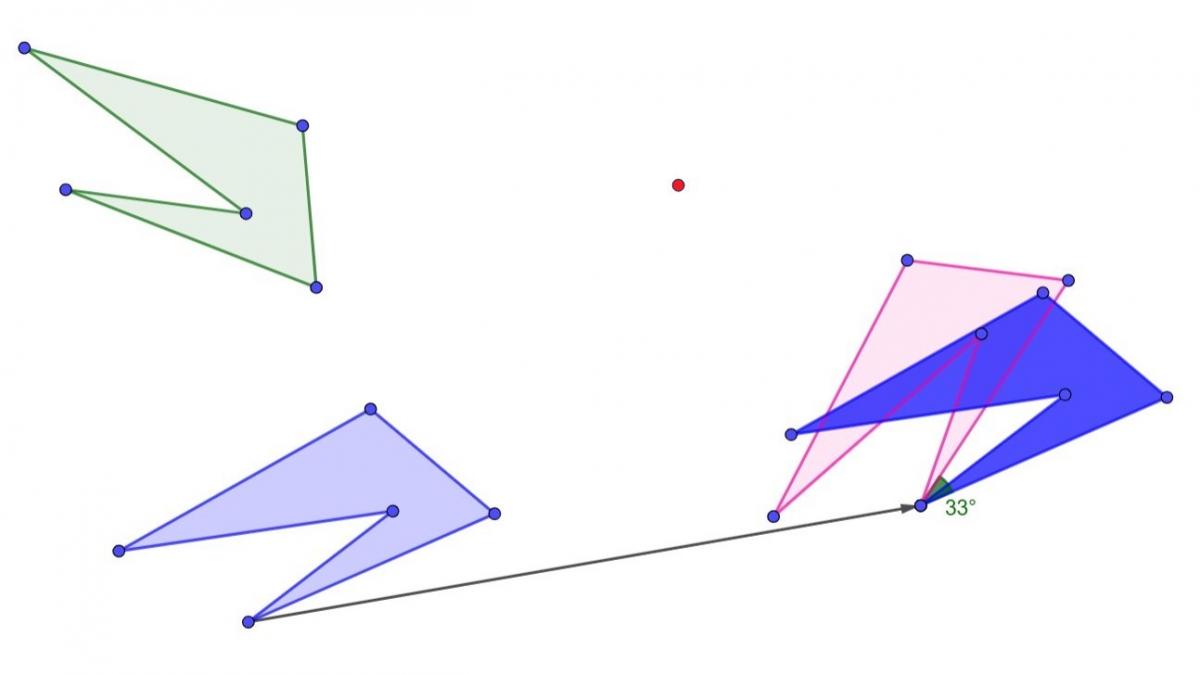
Eksempler (rosa og grønn er originalfigurene)

Etter en rotasjon om det røde punktet (til lyseblå femkant) og en parallellforskyving (til mørkeblå femkant), gjenstår kun en rotasjon på `33^@` før eleven er i mål.

Eleven har tegnet midtnormaler mellom samsvarende punkter, og deretter rotert om skjæringspunktet ved hjelp av en glider (gul figur). Nå gjenstår kun en speiling, så er eleven i mål.

Oppsummering

Diskuter strategier for å løse slike oppgaver, og la elevene dele av egne erfaringer. Noen har kanskje oppdaget at oppgavene ikke blir vanskeligere av at de bruker mange kongruensavbildninger. Hvorfor er det slik? Og finnes det et minste antall kongruensavbildninger for å komme fra den ene figuren til den andre? Det er faktisk mulig å løse alle oppgavene med maksimalt to kongruensavbildninger. Utfordre elevene til å teste om det stemmer i GeoGebra.