Innredning av soverom

Beskrivelse av opplegget

Læreren presenterer oppgaven for elevene og svarer på oppklarende spørsmål. Vi anbefaler at elevene jobber i grupper på to-tre elever, men det er også mulig å gjøre oppgaven individuelt.

Elevene vurderer selv hvilke plakater de vil bruke i forslaget, men det er viktig at de begrunner det godt både matematisk og praktisk. Noen elever kan legge stor vekt på det de mener er estetisk pent. Det er derfor viktig at de også greier å begrunne sine valg ved hjelp av matematisk argumentasjon og hva som er praktisk mulig.

Elevene kan løse oppgaven på forskjellige måter og vil med stor sannsynlighet vektlegge ulike områder i sine løsninger. Noen elever vil kanskje prioritere det estetiske, mens andre kun ser på hva som er matematisk mulig. Det er derfor viktig at elevene begrunner sine valg underveis i arbeidet. Spørsmål som læreren kan stille for å bevisstgjøre elevene på sine valg kan være:

• Er det vanlig å plassere bilder/plakater under et vindu?
• Hvor bør dartskiven plasseres i forhold til vindu og skråtak?
• Er det områder på veggen som ikke er egnet til plakater og/eller dartskive?

Vi anbefaler at det settes av tid til at elevene/gruppene får presentert noen av forslagene. Løsninger som er forskjellige, men som likevel er innenfor rammene av oppgaven kan danne et godt grunnlag for diskusjon, der matematisk argumentasjon åpner eller begrenser mulighetene for det som er praktisk mulig. En slik type diskusjon kan også hjelpe læreren i vurderingen av elevene. Etter eller under presentasjonen kan også læreren utfordre elevene på noen spørsmål som de kan reflektere over:

• Burde Martin vurdert færre plakater?
• Bør plakater og dartskive henge på samme vegg?
• Hvordan hadde det blitt hvis vi ikke skulle tenkt på det estetiske, men bare plassert plakatene og dartskiva der det er plass?

Oppgave til elevene

Martin skal innrede veggen på rommet sitt. Veggen er 3,80m lang og 2,40m høy, men den ene siden av veggen er skrå på grunn av skråtaket. I tillegg er det et vindu på veggen. Målene ser du på tegningen under. Martin planlegger å henge opp fem plakater og en dartskive på veggen, men er usikker på om han får plass og hvordan han skal henge opp tingene sine på en praktisk og pen måte.

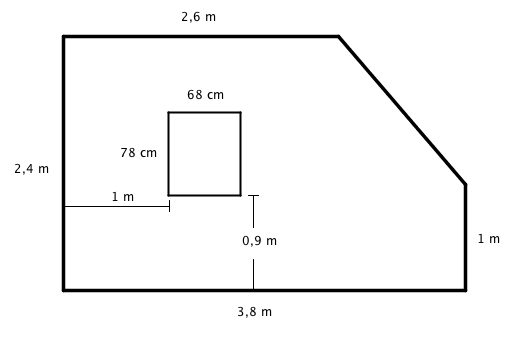
Plakatene Martin har sett seg ut og dartskiva har følgende mål oppgitt i cm:

-       167 x 53                    -   61 x 91

-       71 x 185                    -   53 x 157

-       30 x 90                       -   46 x 61

-       140 x 99                    -   122 x 81

-       Dartskiva har en radius på 24 cm

Lag et forslag til hvilke plakater Martin får plass til og hvor de skal plasseres sammen med dartskiva på veggen

Vurdering

Læreren vurderer elevene etter utvalgt kompetansemål. Det er viktig at det blir satt klare mål for timen og at elevene er kjent med dette, og hvilke kriterier de blir målt etter. I dette undervisningsopplegget kan eksempler på slike mål være:

• Konstruere sammensatte geometriske figurerer.
• Beregne areal av sammensatte geometriske figurer.
• Arbeide med ulike måleenheter og forstå omgjøring mellom cm og m, og cm² og m².
• Bruke og endre målestokk.
• Anvende matematisk kompetanse i arbeid med praktiske problemstillinger.

Elevenes argumentasjon vektlegges spesielt i dette opplegget. Elevene må argumentere for de valgene de gjør når de plasserer plakatene og dartskiva. Argumentene må begrunnes matematisk for eksempel med bruk av konstruksjon og beregning av areal, men også det praktiske og estetiske bør vektlegges noe.

Læreren gir tilbakemelding til elevene underveis i arbeidet, og utfordrer elevene med spørsmål til deres arbeid (se eksempler på spørsmål under ”beskrivelse av opplegget”).

Samspillet mellom å stille elevene reflekterende spørsmål og konkrete tilbakemeldinger på hvordan de kan forbedre sitt arbeid underveis kan danne et godt grunnlag for å vurdere elevenes forståelse, samtidig som elevene reflekterer over eget arbeid.

Hvis det legges opp til en presentasjonsrunde på slutten av timen kan læreren legge opp til klassediskusjon om valg av ulike løsningsstrategi, der elevene diskuterer strategienes likheter og forskjeller. Slike diskusjoner kan gi læreren mulighet til å ta del i elevenes tenkning og avdekke misoppfatninger.

Helhetlig problemløsningsprosess

Gjenkjenne og beskrive

I dette undervisningsopplegget må elevene gjenkjenne bruk av geometri for å beregne areal av veggen, plakatene og dartskiva. Elevene må også gjenkjenne at de må bruke målestokk til å lage et forslag med riktige mål til Martin. For å lage et godt forslag til Martin må elevene derfor lage en matematisk modell som tar høyde for de ulike variablene.

Bruke og bearbeide

Elevene må bearbeide tallene for at de skal kunne bruke dem i den matematiske modellen. Det kan for eksempel være å gjøre om enhetene og velge hvilke plakater som skal være med i forslaget. Elevene må også avgjøre i hvilken målestokk de ønsker å bruke og bearbeide tallene etter det.

Reflektere og vurdere

Når elevene har funnet en matematisk løsning må de vurder om svaret er matematisk riktig. Slev om plakatene og dartskiva arealmessig får plass på veggen kan vinduet og den skrå veggen gi utfordringer som gjør at plakatene må kutte opp for at matematiske løsningen skal stemme. Elevene må også vurdere om den matematiske løsningen gir en god praktisk løsning på problemet til Martin.

Kommunisere

Kommunikasjon er gjennomgående i hele problemløsningsprosessen. Elevene må kommunisere og diskutere hvilke matematiske modeller de skal bruke og argumentere for valgene de tar. Videre må de presentere arbeide sitt for resten av klassen på en slik måte at de andre elevene forstår hvordan de har tenkt når de kom fram til sin løsning.