Sortering av firkanter
Emne
Geometri
Hensikt
Elevene skal samtale og diskutere forskjellen mellom nødvendige og tilstrekkelige egenskaper i definisjon firkanter.
Valg av tidspunkt
Du trenger
Elevark med figurer til å klippe ut. Velg mellom figurene med navn eller figurene uten navn.
Aktiviteten
Aktivitet 1
-
Hvis du velger å bruke figurene uten navn skal elevene først sette navn på figurene.
- Elvene skal notere egenskaper som de mener er typiske for figuren.
Vanlige svar kan være:
Rektangel:
- to og to sider er parallelle
- alle vinkler er 90°
- diagonalene er like lange
- diagonalene halverer hverandre
Kvadrat
- alle fire sider er like lange
- alle vinkler er 90°
- diagonalene er like lange
Parallellogram
- …
Rombe
- …
Trapes
- …
Drage
- To og to sider er like lange
- Diagonalene står normalt på hverandre
- I samtalen etterpå kan læreren oppfordre elevene til å se om alle egenskapene er nødvendig for å beskrive en av firkantene ovenfor. Er det noen egenskaper som er felles for flere firkanter?
Kommentar til læreren
For veldig mange elever er rektangler og kvadrater sidestilte figurer. Begge er firkanter med 4 rette vinkler. Det er ikke innlysende at kvadrater er spesialtilfeller av rektangler. Et tips kan være at man spør elevene om to og to sider er parallelle i et kvadrat. Svaret er ofte ja, …. men i et rektangel er ikke sidene like lange. Det tar tid til å få elevene til å forstå at man bare spør om sidene er parallelle og ikke spør etter lengden på sidene.
Aktivitet 2
Alle rektangler er firkanter, men ikke alle firkanter er rektangler.
Alle kvadrater er rektangler, men ikke alle rektangler er kvadrater
- Start opplegget med en fellessamtale om betydningen av setningene. Bruk god tid med elevene slik at de forstår innholdet. I det følgende skal de legge figurene i rekkefølge slik at de kan lage tilsvarende setninger bare ved å bytte ut navnet til firkantene.
| Parallellogram | Rektangel |
| To og to sider er like | To og to sider er like lange |
| To og to sider er parallelle | To og to sider er parallelle |
| Diagonalene er like lange | |
| Alle vinkler er 90° |
Rektangelet har alle egenskaper til parallellogrammet. Derfor er alle rektangler parallellogram men ikke alle parallellogram er rektangler.
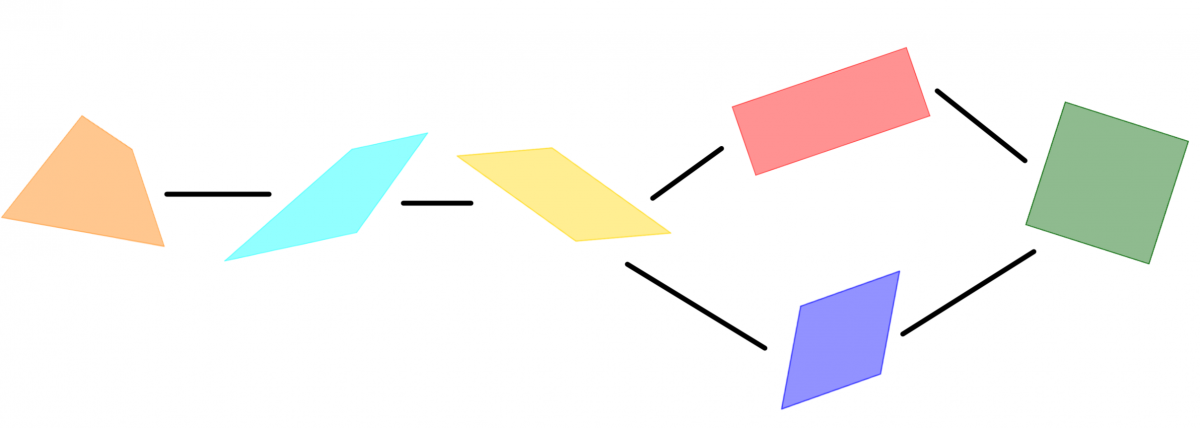
- La elevene sortere figurene.
Forslag for sortering:
- Kontroller om elevene har forstått det ved å spørre setninger som:
Hvorfor vet du at:
- Alle kvadrater er trapeser?
- Alle romber er parallellogram?
- Alle kvadrater er rektangler?
- …
- Avslutt med å la elevene lage sin egen oversikt med figurer og sammenhengen mellom dem.
Kommentar til læreren
I et første forsøk plasserer elevene gjerne den uregelmessige firkanten, parallellogrammet, rektangelet og kvadratet i riktig rekkefølge. Trapeset er de mer ukjent med, men etter litt samtale om egenskaper går det greit.
Mange elever vil slite med å plassere romben, da figuren ikke kan settes mellom to figurer. Elevene må da lage en veiskille som samles igjen ved kvadratet
Hvis man gjennomfører denne aktiviteten på barnetrinnet kan det være lurt å ta bort dragen i første omgang. Det er figuren som elevene er minst vant med.
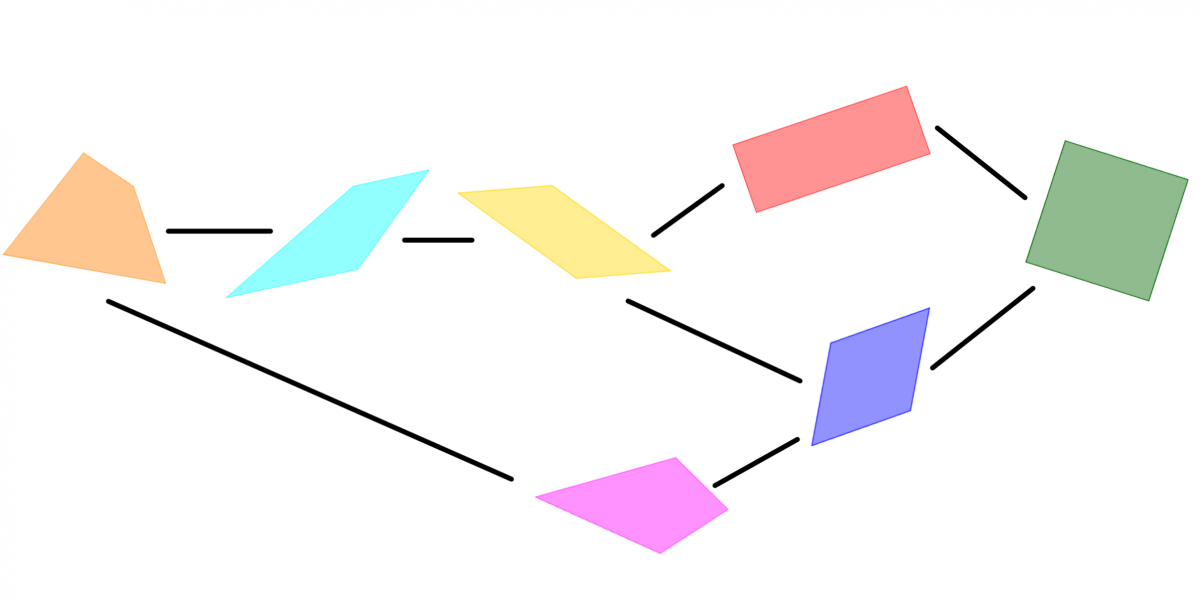
Forslag med drage:
- Hvis læreren vil legge vekt på implikasjon og direkte bevis, kan det brukes eksempler som:
Vis at et kvadrat er et parallellogram.
Vis at et kvadrat er et trapes.
Vis at et parallellogram er et trapes.
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 9.trinn
- utforske og argumentere for korleis det å endre føresetnader i geometriske problemstillingar påverkar løysingar
- Kompetansemål etter 6. trinn
- beskrive eigenskapar ved og minimumsdefinisjonar av to- og tredimensjonale figurar og forklare kva for eigenskapar figurane har felles, og kva for eigenskapar som skil dei frå kvarandre