Tegn en dynamisk, rettvinklet trekant

Dynamisk geometri, trekant, rettvinklet trekant, Tales’ setning.

PC med GeoGebra.

Elevene arbeider i par eller små grupper slik at de kan diskutere underveis. Alle bruker hver sin PC med GeoGebra. Sørg for at elevene tar bort koordinatsystem og rutenett, samt at de har sortert objekter etter type og ikke får navn på nye objekt. Se Lær GeoGebra for veiledning (for eksempel GeoGebra-tips for lærere). 

Aktivitet

Oppgave til elevene:

• Tegn et linjestykke med lengde 9,4.
• Tegn en rettvinklet trekant. Linjestykket skal være en side i trekanten.  
• Vis vinklene.
• Dra i trekanten. Er trekanten alltid rettvinklet?
• Kan start-linjestykket være katet i trekanten? Kan det være hypotenus?

Kommentar til læreren

Gi oppgaven muntlig. Skriv gjerne stikkord på tavle eller storskjerm. Forklar begrepene katet og hypotenus om elevene ikke kjenner disse.

Hvis elevene har lite erfaring med GeoGebra, kan det være lurt å starte med å lage linjestykket i hel klasse. Vurder også om elevene skal starte med et linjestykke uten fast lengde. Da vil trekanten bli mer dynamisk, men det vil være mer utfordrende for elevene å fokusere på den rette vinkelen. Elevene bør lage et nytt linjestykke for hver trekant de undersøker. Minn de på å bevege et objekt om gangen.

I denne aktiviteten er det lettest å tegne trekanten hvor start-linjestykket er en katet. Elevene kan for eksempel tegne en normal linje i et av punktene. Eller de kan lage en vinkel med fast størrelse (90°) i et av punktene. Begge måter gir en dynamisk, rettvinklet trekant.

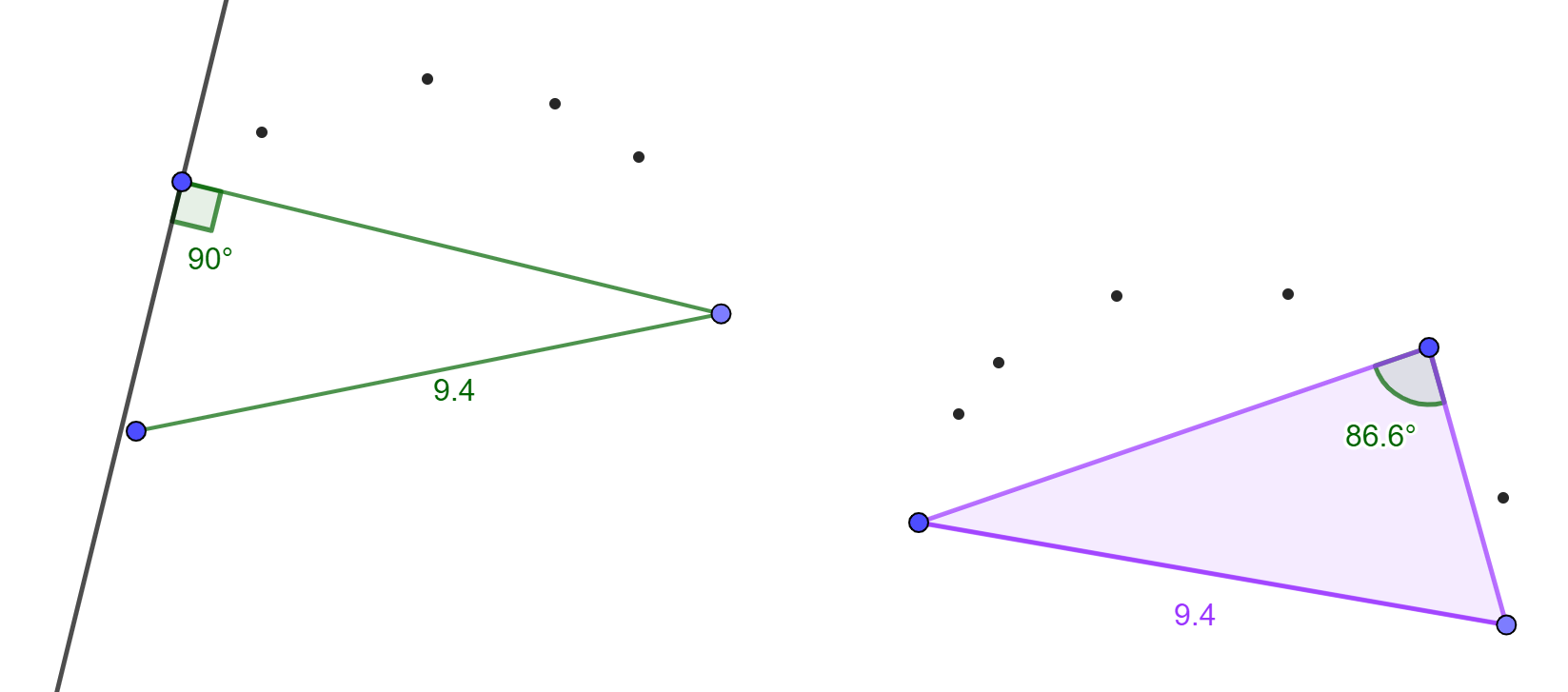
Det er mer krevende å lage en trekant hvor start-linjestykket er hypotenus. Elevene starter med å lage et linjestykke som skal være hypotenus. Da vet de at de to andre sidene i trekanten skal være kateter og at vinkelen mellom disse er 90°. Så kan elevene for eksempel tegne en av katetene, lage en normal i endepunktet og forsøke å få linjen til å treffe endepunktet til hypotenusen (se grønn figur). Eller de kan lage en trekant (Mangekant) og forsøke å få vinkelen mellom sidene til å bli 90° (se lilla figur).

Det er lurt å tipse elevene om verktøyet Penn. Det kan de bruke til å markere mens de utforsker. Elevene vil oppdage at start-linjestykket kun blir hypotenus hvis det tredje punktet ligger på halvsirkelen over hypotenusen. Denne matematiske sammenhengen heter Tales’ setning. Den er oppkalt etter Tales fra Milet (ca. 625 f.Kr – ca. 545 f.Kr) som regnes den første matematikeren og den første naturvitenskapsmannen (https://no.wikipedia.org/wiki/Tales_fra_Milet). Når elevene har oppdaget sammenhengen, kan de lage en dynamisk, rettvinklet trekant med hypotenusen som start-linjestykke.

Noen elever glemmer å bruke de matematiske egenskapene når de skal lage en dynamisk, rettvinklet trekant. Disse tegner enda et linjestykke (i et av punktene) som de drar slik at vinkelen mellom linjestykkene er 90°. Når elevene drar i trekanten, vil de oppdage at den ikke alltid er rettvinklet. At vinkelen endrer seg, er en god anledning til å snakke om egenskapene til rettvinklede trekanter og hvordan vi må bruke dem for å lage en dynamisk figur.

Oppsummering

Som oppsummering skal elevene vise fram hvordan de har tenkt, og hvilke matematiske sammenhenger de har funnet. Velg ut elevene som skal presentere arbeidet sitt basert på observasjonene underveis. Pass på at klassen får se forskjellige løsningsmetoder, både med linjestykket som katet og som hypotenus.

Elevene vil ha stor nytte av å kunne lage dynamiske, rettvinklede trekanter når de senere skal bli kjent med Pytagoras’ setning.