Tre på rad – brøk og prosent

Brøk og prosent.

Dette opplegget er utarbeidet etter idé fra Sirkel 9.

To vanlige terninger (1-6) og seks spillebrikker til hver spiller.

Spillebrett.

To – tre elever spiller sammen på ett spillebrett.

Spillerne kaster etter tur to terninger og lager en brøk der verdien på den ene terningen er teller, og den andre er nevner. Elevene skal bedømme størrelsen av brøken de lager, finne den prosenten som svarer til brøken og legge en av brikkene på ei rute som viser denne prosenten. Eksempel: Terningene viser 3 og 4. Du kan lage brøken `(3)/(4)` og legge brikken på 75 %, eller `(4)/(3)` og legge brikken på `133(1)/(3)%`.

Dersom ingen ledige ruter passer til prosentene du kan lage, legger du brikken på ei av rutene med smilefjes. Når alle seks brikkene er lagt ut, flytter du en av brikkene som står på brettet. Spillet fortsetter til en av spillerne har fått tre på rad: vannrett, loddrett eller diagonalt.

Matematiske sammenhenger

Når vi jobber med sammenhengen mellom brøker, desimaltall og prosent må de betraktes som ulike symbolske representasjoner av samme forholdstall. Denne kunnskapen er nyttig i mange sammenhenger, for eksempel hvis man skal regne 25 % av 120. Man kan bare dele på fire, dersom man vet at en firedel er det samme som 25 %. På samme måte kan man tenke på 10 % som en tidel, så da kan man bare dele på 10 for å finne 10 %. Denne kunnskapen kan man bruke i videre beregninger. Vet man 10 %, så er halvparten av det 5 %. Så for å finne 5 % kan man dele på 10 og deretter dele på to. Det er til stor hjelp for elevene å få mange slike erfaringer som de kan bruke som referanser i arbeid med brøk og prosent. Med utgangspunkt i kjente erfaringsreferanser som null, en halv og en hel, kan elevene bygge flere referanser som en firedel, en tidel, en femdel, en seksdel, tre firedeler osv.

I spillet Tre på rad – brøk og prosent skal elevene finne sammenhenger og forklare og begrunne omgjøringene de gjør. Elevene kan også etterhvert studere spillbrettet og diskutere tallene som er valgt. Hvorfor er det akkurat de prosentene? Hvorfor er noen av dem oppført flere ganger?

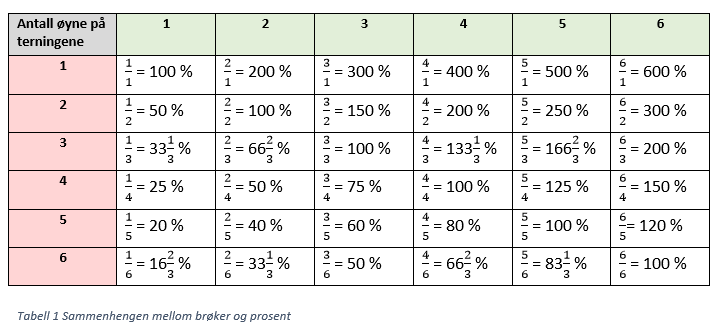
Tabell 1 viser en oversikt over brøkene elevene kan lage når de bruker to vanlige terninger (1-6). Med utgangspunkt i kjente sammenhenger som for eksempel at halvparten kan uttrykkes som både `(1)/(2)` og 50 %, kan elevene resonnere seg fram til hvilken prosent som stemmer med brøken de har valgt.

Eksempel: Lise har laget brøken `(4)/(3)`. Hun forklarer at det må være mer enn 100 % og mindre enn 150 %, fordi "tre tredeler" er 100 % og "fire og en halv tredel" er 150 %. Lise vet at en tredel er det samme som 33,33 (med uendelig mange desimaler), så da må `133(1)/(3)%` være riktig. Hun legger brikken sin på `133(1)/(3)%`.

Dersom en ønsker å utvide spillet, kan elevene bruke andre terninger (0-9, 1-12 eller 1-20). Spillbrettet må da tilpasses de nye brøkene. Å finne ut hvilke prosenter som skal stå på spillbrettet kan være en fin oppgave for elevene.