Trekanter med samme areal

PC med GeoGebra

Elevene arbeider i par eller små grupper slik at de kan diskutere underveis. Alle bruker hver sin PC med GeoGebra. Sørg for at elevene tar bort koordinatsystem og rutenett, samt at de har sortert objekter etter type og ikke får navn på nye objekt. Se Lær GeoGebra: GeoGebra-tips for lærere for veiledning.

Aktivitet

Oppgave til elevene:

• Tegn en trekant.
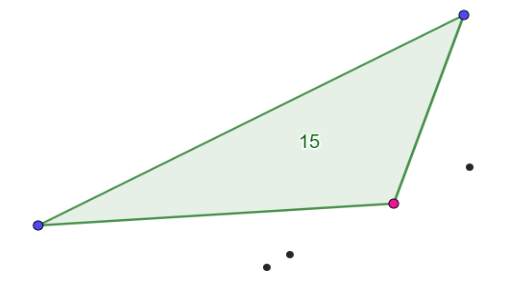
• Vis arealet og dra i trekanten til arealet blir 15.
• Bruk verktøyet Penn og sett et merke i et av hjørnene.
• Dra i dette hjørnet til du finner en ny trekant med areal 15.
• Merk plasseringen til hjørnet med Penn.
• Fortsett på samme måte. Dra alltid i det samme hjørnet!
• Observer og lag en hypotese.
• Tegn en ny trekant for å bekrefte/avkrefte hypotesen.

Kommentar til læreren

Gi oppgaven muntlig. Skriv gjerne stikkord på tavle eller storskjerm.

Hvis elevene har lite erfaring med GeoGebra, kan det være lurt å lage trekanten i hel klasse og vise hvordan verktøyet Penn fungerer. Det er viktig at elevene drar i det samme hjørnet når de utforsker. De kan godt gi punktet en annen farge slik at det skiller seg fra resten. Minn elevene på at de må velge Flytt før de leter etter en ny trekant.

Mange elever vil lage en hypotese om at trekanten får samme areal når punktet de beveger ligger på en linje parallell med motstående side. Men stemmer det alltid? Elevene kan teste hypotesen ved å ta utgangspunkt i trekanten de allerede har laget. Først tegner de en linje som går gjennom punktet de har beveget og som er parallell med motstående side i trekanten (grunnlinjen). Så lager de en ny trekant som har samme grunnlinje og som har det tredje punktet på den parallelle linjen.

De kan også teste hypotesen ved lage to parallelle linjer. Så tegner de en trekant som har hjørnene på linjene. Hvis elevene bruker punktene som er på de parallelle linjene fra før når de tegner trekanten, blir det vanskelig å bruke figuren til å undersøke hypotesen. Da styrer nemlig punktene både plasseringen av de to parallelle linjene og av trekanten. Tips elevene om å lage en trekant uten å bruke punktene i stedet.

Oppsummering

Som oppsummering skal elevene vise fram hvordan de har tenkt, og hvilke matematiske sammenhenger de har funnet. Velg ut elevene som skal presentere arbeidet sitt basert på observasjonene underveis. Pass på at klassen får se løsningsmetoder der ulike hjørner blir brukt.

Opplegget kan gi elevene en dypere forståelse av sammenhengen mellom grunnlinje, høyde og areal i trekanter. Avstanden mellom to parallelle linjer er konstant, og i en trekant er denne avstanden høyden. Fortsett gjerne med noen av aktivitetene fra Trekant med areal 12.