Eksponentialfunksjoner med hyssing

Emne
Eksponentialfunksjon
Visualisering av egenskaper ved eksponentialfunksjonen ved hjelp av hyssinglengder.
Utviklet ved Molde videregående skole
Hensikt
Ved å klippe og sammenlikne hyssinglengder arbeider elevene med eksponentialfunksjon med positiv og negativ vekstfaktor.
Du trenger
Uelastisk hyssing, saks, tommestokk, ruteark
Aktiviteten
Klippe biter av tauet
Elevene kan gjerne arbeide i grupper, 2-3 elever per gruppe er fint.
1. Start med å klippe til en hyssing som måler nøyaktig 100,0 cm.
2. Klipp av 20% av hyssingen. Ta vare på den avklipte biten,
mål restlengden så nøyaktig som mulig og noter den i tabellen under.
3. Klipp av nøyaktig 20% av det som er igjen av hyssingen.
Ta vare på den avklipte biten og noter restlengden i tabellen.
4. Gjenta til du har klipt av 8 biter.
| Klipp nr (x) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Restlengde(cm) | 100,0 |
5. Finn en modell for restlengden etter at du har klipt av x biter.
| R(x)= |
6. Hvor mange ganger må du klippe for at hyssingen skal være halvert?
Undersøke de avklipte bitene
1) Legg nå de avklipte bitene etter hverandre på et ruteark. Start fra venstre med den minste biten (den du klipte av sist), og legg bitene etter hverandre i stigende rekkefølge bortover. La det være 1 cm mellom hver bit, og la nederste enden på alle bitene starte på ei vannrett linje nederst på rutearket. Hvis hyssingbitene krøller seg kan du merke av på rutearket hvor toppen av hyssingbiten skal være.
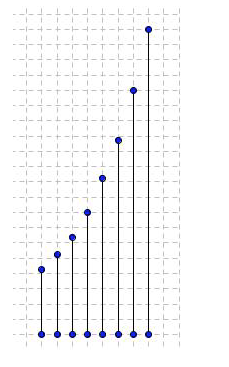
2) Mål lengden av bitene og noter lengdene i tabellen under.
| Bit nr (x) | 0 (den minste) | 1 | 2 | 3 | 4 | 5 | 6 | 7 (den lengste) |
| Lengde (cm) |
3) Finn en matematisk modell for lengden av de avklipte bitene. Sammenlikn med modellen R(x) som dere fant tidligere, og tenk over hvorfor vekstfaktoren blir som den blir.
| B(x)= |
4) Er det mulig å få en bit på nøyaktig 100 cm ved hjelp av denne modellen? Ville det vært mulig hvis vi hadde klipt av flere biter?
Finn historien om Akilles og skilpadden på Internet hvis du ikke kjenner den fra før. Hvordan likner den historien på det vi har arbeidet med her?
Det er viktig å være nøyaktig med klipping og måling for å få bra resultat.
De målte verdiene bør bli omtrent slik:
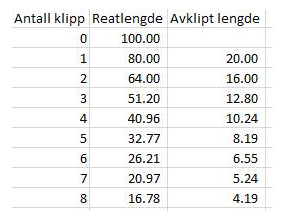
Restlengde etter x klipp:
Lengden av de avklipte bitene:
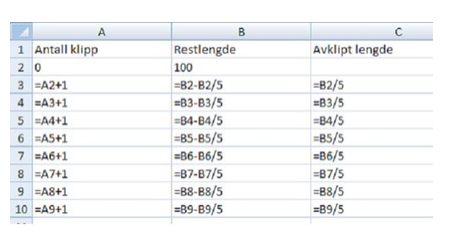
De matematiske modellene kan også finnes ved hjelp av eksponentiell regresjon på lommeregneren.
Om ønskelig kan modellen lages i regneark, formlene blir slik:
Rammeplanmål/Kompetansemål
- Videregående
- R1
- modellere og analysere eksponentiell og logistisk vekst i reelle datasett
- R2
- gi eksempler på ulike situasjoner som kan modelleres ved å bruke ulike matematiske funksjoner, og modellere og analysere slike situasjoner ved å bruke reelle datasett
- S2
- modellere og analysere eksponentiell og logistisk vekst i reelle datasett
- Vg1P
- tolke og bruke funksjonar i matematisk modellering og problemløysing
- bruke digitale verktøy i utforsking og problemløysing knytt til eigenskapar ved funksjonar, og diskutere løysingane
- Vg1T
- utforske og beskrive eigenskapane ved polynomfunksjonar, rasjonale funksjonar, eksponentialfunksjonar og potensfunksjonar
