Introduksjon til skalarprodukt

Vektor, skalar, skalarprodukt, prikkprodukt.

PC med GeoGebra og elevark.

Aktivitet 1

Følgende ord vises for elevene: vektor, skalar og produkt. Elevene jobber individuelt i 2-3 minutter. De skal notere ned forklaringer på ordene uten å bruke hjelpemidler.

I en felles klassesamtale noterer læreren alle ord og uttrykk som blir nevnt på tavla. På forhånd bør hun ha forberedt en oversikt over hvilke ord og uttrykk hun forventer at elevene kommer med og laget en plan for hvordan hun vil sortere dem.

Mulige elevsvar:

• Skalar: tall, det vanlige
• Produkt: multiplikasjon, faktorer, gangetabellen, ganging
• Vektor: lengde, retning, kraft, fysikk, [1,2], `((1),(2)), <1,2>, veca`

Deretter presenterer læreren læringsmålet for timen ved å notere følgende på tavla:

Skalarprodukt

vektor · vektor = skalar

Kommentarer til læreren

Undervisningen starter med noe som er kjent, noe som hjelper elevene med å sette det nye i sammenheng med det de kan fra før. Læreren kan gjerne tipse elevene om at ordet skalarprodukt består av to deler. De kjenner ikke til ordet skalarprodukt, men de kjenner til delene, skalar og produkt.

Til slutt kan læreren skrive læringsmålet vektor · vektor = skalar og overskriften skalarprodukt på tavla. Målet for timen er å få en forståelse for hva skalarproduktet egentlig er, ikke bare hvordan de regner det ut. Skalarprodukt blir også kalt for prikkprodukt (dot product).

Aktivitet 2

Læreren skriver ned følgende uttrykk på tavla, gjerne på forhånd:

`[3,4] · [5,7] = 43 `

`[2,6] · [4,4] =  32`

`[8, -4] · [5,9] = 4 `

`[2,2] · [-12,5] = -14 `

Elevenes oppgave blir å finne ut hvordan de skal regne ut svaret for å få riktig resultat. De diskuterer fremgangsmåten i par.

Når elevene mener at de har funnet riktig regneregel, kan læreren gi flere oppgaver slik at elevene kan teste om regelen fortsatt stemmer. Læreren kan utfordre elevene til å formulere en regel for å beregne skalarproduktet med ord og algebraisk.

Under læringsmålet kan læreren nå føye til at klassen har funnet en måte beregne skalarproduktet på. Det er viktig å framheve at skalarproduktet er et vanlig tall. Det er ikke selvsagt for elevene. Et mulig svar kan være:

Vi finner skalarprodukt ved å multiplisere førstekoordinatene og addere produktet av andrekoordinatene:

`[a,b] · [c,d] = ac + bd `

Kommentarer til læreren

I denne aktiviteten finner elevene først ut hvordan de regner ut skalarproduktet av to vektorer. Læreren skal ikke forklare fremgangsmåten på forhånd, men la elevene finne ut av det selv. Erfaring tilsier at elevene finner regneregelen ganske fort.  For å være helt sikker på at alle får den tida de trenger til å prøve og feile, er det lurt å ha en del ekstraoppgaver tilgjengelig. Da har alle elevene noe å gjøre enten de regner raskt eller ikke. Det er ikke nødvendig at alle elevene løser alle oppgavene.

Etter at elevene har løst oppgaver og diskutert, skal klassen sammenfatte hvordan de regner ut skalarproduktet. Læreren skriver opp regnemåten med ord og med formel. Bruk begrepene skalarprodukt, vektor og skalar i klassesamtalen. Vær nøye med å notere fremgangsmåten slik elevene vil ha det, uansett om det virker litt kronglete. Det er viktig at elevene øver seg på å formulere matematiske sammenhenger med ord.

Aktivitet 3

På tavla står følgende:

`[  ,  ] · [  ,  ] = 0 `

Oppgaven til elevene er å finne eksempler som gjør at påstanden blir sann. Det er en fordel at de jobber i par. Etter en stund samles eksemplene til elevene på tavla.

Kommentarer til læreren

Gi elevene nok tid til å finne mange eksempler. Elevene tilpasser arbeidet til egne kunnskaper og ferdigheter og eksemplene vil derfor få ulik vanskelighetsgrad. Læreren kan gjerne utfordre elever til å finne to vektorer med ulike tall som har skalarprodukt 0.

I oppsummeringen skal elevene vise fram eksemplene sine og prøve å finne sammenhenger. Noter eksemplene i rekkefølgen de blir nevnt i.

Mulige eksempler fra elevene:

a) `[4 ,2] · [5 ,-10] = 0 `

b) `[2 ,2] · [2 ,-2] = 0 `

c) `[2 ,4] · [6 ,-3] = 0 `

d) `[3 ,4] · [-4 ,3] = 0 `

Svar b) er matematisk sett det enkleste, to like tall og ett minustegn. En rundgang i klasserommet viser derimot at svar av typen d) gjerne forekommer hyppigst. I svar av typen a) og c) har elevene antagelig valgt en annen strategi. De har valgt ett tall og så har de funnet frem til to multiplikasjoner med det valgte tallet som produkt. Elevene vil ganske raskt oppdage at det er nødvendig med negative tall. Kan det være flere negative tall?

Lærerens oppgave er å vise sammenhengen mellom de ulike løsningene. For eksempel at `[6 ,8] · [-4, 3] = 2[3 ,4] · [-4, 3] = 0` og `[4 ,2] · [5, -10] = 2[2 ,1] · 5[1, -2] = 0` er variasjoner av type d).

Aktivitet 4

Elevene arbeider på papir. De velger et regnestykke fra aktivitet 3 og tegner vektorene som hører til i et koordinatsystem. Gi gjerne et startpunkt slik at elevene ikke tegner alle vektorer i origo. Så skal elevene bruke linjal og forlenge vektorene til linjene skjærer hverandre. Be dem å gjøre det samme med flere eksempler. Målet er at elevene oppdager at hvis skalarproduktet er 0, står vektorene vinkelrett på hverandre. Læreren bruker elevenes eksempler som utgangspunkt for klassesamtalen.

Kommentarer til læreren

Noen elever blander sammen punkt og vektor. De tegner en vektor mellom to punkter i stedet for å tegne to vektorer. Det vil si at de blander sammen [  , ] med (  ,  ).  For eksempel tegner elevene ofte [4 ,2] · [5 ,-10] som vektor mellom punkt (4, 2) og punkt (5, -10). Repeter gjerne forskjellen på de to skrivemåtene før elevene starter.

Aktivitet 5

I aktivitet 4 har elevene oppdaget at vektorene står vinkelrett på hverandre hvis skalarproduktet er 0. Nå skal de undersøke om setningen også gjelder motsatt vei. Det vil si at hvis to vektorer står vinkelrett på hverandre, er skalarproduktet 0. Deretter skal elevene undersøke når skalarproduktet blir positivt og negativt. Til slutt blir elevene introdusert for en annen definisjon av skalarproduktet. Oppgaven blir å finne sammenhengen mellom de to uttrykkene for skalarproduktet.

Elevene kan gjerne arbeide i par, men det er viktig at alle bruker GeoGebra og at de skriver på hvert sitt elevark. La elevene jobbe i eget tempo. Det er ikke nødvendig at elevene har løst alle oppgavene før klassen begynner med oppsummeringen.

Oppgave 1

• Tegn tre vektorer med ulik lengde på hver av de to linjene og gi dem navnet `veca, vecb...`
• Noter vektorene med vektorkoordinater i tabellen.
• Velg én vektor fra hver av linjene og regn ut skalarproduktet. Lag minst fire eksempler.
• Noter dine matematiske observasjoner. 

Oppgave 2

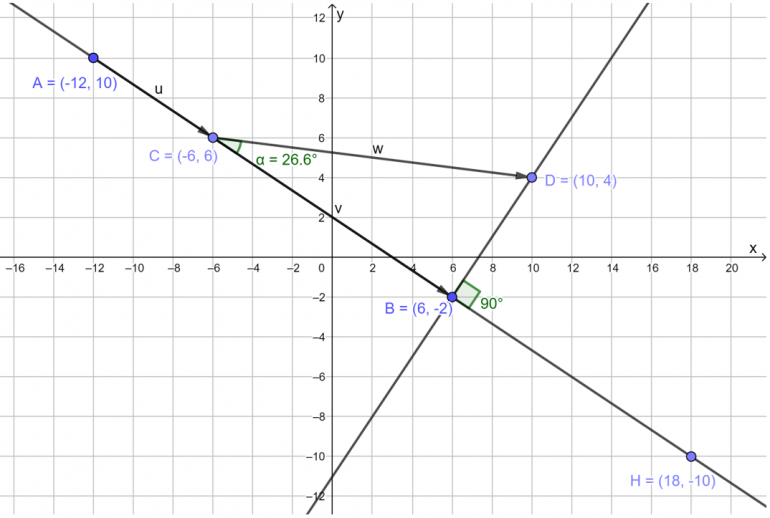
• Lag en figur som tilsvarer denne figuren i GeoGebra. Tallene dine vil være forskjellige fra tallene på bildet.
• Undersøk hvordan skalarproduktet endrer seg når du endrer vinkelen mellom vektorene. Bruk matematiske begreper når du noterer observasjonene dine.

Oppgave 3 

Formelen for skalarprodukt blir ofte oppgitt slik: `vecu · vecv = |vecu| · |vecv| · cos alpha` der `alpha`er den minste vinkelen mellom de to vektorene.

• Forklar formelen med ord.
• Hvorfor blir skalarproduktet 0 når vektorene står vinkelrett på hverandre? Ta utgangspunkt i formelen og skriv ned din matematiske tankerekke.

Oppgave 4

Nå skal du utforske sammenhengen mellom formelen `vecu · vecv = |vecu| · |vecv| · cos alpha` og det du har lært om skalarprodukt så langt. 

• Lag tegningen i GeoGebra. Bruk samme punkter.
• Bruk vektorkoordinatene til å regne ut `vec(AC) · vec(CB)` og `vec(AC) · vec(CD)`
• Bruk navnet til vektorene og gjør de samme beregningene i Algebrafeltet. Dra svarene inn i Grafikkfeltet. Tips: Det er lettere å holde oversikt om du endrer navnene til uw og uv.
• Bruk navnet til vektorene og regn ut `|vec(AC)| · |vec(CD)| · cos alpha`. Gi svaret navnet uwcos og dra uttrykket inn i Grafikkfeltet.
• Dra i figuren for å se om sammenhengen som du har funnet alltid stemmer.
• Bruk matematiske begreper til å forklare hvorfor alle utregningene gir det samme svaret.

Kommentarer til læreren

La elevene arbeide i eget tempo. Det er ikke nødvendig at alle kommer helt i mål før oppsummeringen.

I aktivitet 4 fant elevene ut at vektorene står vinkelrett på hverandre hvis skalarproduktet er 0.

I oppgave 1 utforsker elevene den motsatte sammenhengen. Altså hvis to vektorer står vinkelrett på hverandre, er skalarproduktet 0. Det er viktig å poengtere at akkurat denne setningen gjelder begge veier, men at det ikke er slik for alle matematiske sammenhenger.

I oppgave 2 skal elevene bruke GeoGebra til å utforske verdien til skalarproduktet. Observasjonene skriver de ned på elevarket. Læreren går rundt i klasserommet for å se hvordan elevene formulerer svarene sine. På den måten kan hun bestemme en hensiktsmessig rekkefølge for presentasjonen av elevenes svar og begrunnelser.

I oppgave 3 blir elevene presentert for formelen for skalarproduktet. Først blir de bedt om å forklare formelen med ord, altså hva formelen sier at de skal gjøre for å regne ut skalarproduktet. Så må elevene bruke trigonometri til å forklare hvorfor skalarproduktet er 0 når vektorene står vinkelrett på hverandre. Elevene lærte om trigonometriske sammenhenger i 1T.

Målet med oppgave 4 er å forklare hvorfor tre forskjellige utregninger kan gi det samme svaret. Oppgaven er omfattende og trenger en god oppsummering. Elevene starter med å tegne en gitt figur i GeoGebra. De bruker det som de har lært for å beregne skalarproduktet på papir. Etterpå gjør elevene de samme beregninger i Algebrafeltet. Elevene vil oppdage at de tre regnestykkene gir samme verdi, uansett om de drar i figuren. At u×v og u×w gir det samme resultatet strider mot elevenes erfaringer fra multiplikasjon. De ser at jo at vektor w er lengre enn vektor v, noe som også skulle tilsi at skalarproduktet blir større.                                                                                                                       

Ved å bruke kunnskap fra 1T om at `|vecv| = |vecw| · cos alpha` kan elevene vise sammenhengen mellom de to uttrykkene for skalarproduktet. Dette er en god anledning til å diskutere hva det betyr at vektorer har både lengde og retning.

Måten vektorene er tegnet på viser sammenhengen `|vecv| = |vecw| · cos alpha` tydelig. Projeksjonen av vektor w på samme linje som vektor u henger da sammen med oppdagelsen av at skalarproduktet er størst når vektorene peker i samme retning, altså når α er 0˚ (cos 0˚ = 1). Og at skalarproduktet er 0 når vektorene står vinkelrett på hverandre, altså når α er 90˚ (cos 90˚ = 0)

Under oppsummeringen er det en fordel at læreren kan vise fram og arbeide med figuren. Gi skalarproduktene navn etter vektorene som er brukt i utregningen. For eksempel uv som navn for skalarproduktet u∙v.

Oppsummeringen bør vektlegge at:

• En vektor er bestemt ved både lengde og retning.
• Koordinatformen viser både lengden og retningen til vektoren.
• Skalarproduktet blir 0 når vinkelen mellom vektorene er 90°, altså når vektorene står vinkelrett på hverandre.
• Skalarproduktet blir størst når vektorene peker i samme retning.
• Fordelene og ulempene ved de ulike formlene

Som avslutning kan elevene bevise at sammenhengen mellom formlene gjelder når to vektorer peker i samme retning, altså når α er 0˚.

Forslag til bevis

Vi har to vektorer `vecu = [a,b]` og `vecv = [c,d]`. Skalarproduktet til vektorene er `vecu · vecv = ac + bd`. Siden vektorene skal peke i samme retning, men kan ha ulik lengde, kan vi skrive `vecv = [c,d] = [na,nb]`.

`vecu · vecv = |vecu||vecv| cos alpha`  

                     =  ​​​​|[a, b]| |[na,nb]| cos 0°`  

                     = `(sqrt(a^(2)+b^(2)))  (sqrt((na)^(2)+(nb)^(2))) · 1`

                     = `sqrt((a^(2)+b^(2))(n^2a^(2)+n^2b^(2))`

                     = `sqrt((a^(2)+b^(2))(a^(2)+b^(2))n^2 `

                     = `(a^(2)+b^(2))n`

                     = `a(na)+b(nb)`

                     =  `ac + bd`