Oppgavestreng 12 ∙ 149

Emne
Utvikle effektive strategier i arbeid med tall og regneoperasjoner.
Begrunne strategier på enkelteksempler.
Dette opplegget er utviklet som en del av prosjektet Mestre Ambisiøs Matematikkundervisning.
Hensikt
Utnytte snille tall i multiplikasjon. Bruke ulike representasjoner av tall og regneoperasjoner. Gjennom diskusjoner om relasjoner mellom ulike multiplikasjonsstykker, vil opplegget også kunne bidra til å utvikle mer effektive strategier for multiplikasjon. Oppgavestrengen kan også brukes til å generalisere den distributive egenskap.
Valg av tidspunkt
Du trenger
Tavle.
Aktiviteten
 Læreren skriver oppgavene en og en på tavla. Når de fleste elevene viser at de har tenkt ferdig, spør læreren hvordan de kom fram til svaret. Læreren noterer elevenes tenkemåte med symbolsk notasjon og en representasjon og leder diskusjonen om de ulike strategiene. I diskusjonen fremhever læreren strategien der man utnytter de to første regnestykkene i arbeid med de to siste.
Læreren skriver oppgavene en og en på tavla. Når de fleste elevene viser at de har tenkt ferdig, spør læreren hvordan de kom fram til svaret. Læreren noterer elevenes tenkemåte med symbolsk notasjon og en representasjon og leder diskusjonen om de ulike strategiene. I diskusjonen fremhever læreren strategien der man utnytter de to første regnestykkene i arbeid med de to siste.
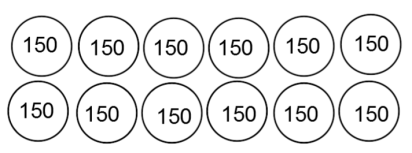
De to siste oppgavene i oppgavestrengen kan løses ved å ta i bruk svar elevene har funnet i tidligere oppgaver. Regnestykket 12 · 150 kan løses ved å legge sammen produktene av 2 · 150 og 10 · 150. Begrunnelse for hvorfor dette er riktig kan illustreres med 12 «poser» med 150 «kuler», rutenett eller areal.
 I den siste oppgaven kan elevene bruke svaret fra 12 · 150 til å regne ut 12 · 149. Både posene, rutenettet eller areal kan brukes til å illustrere oppgaven. Læreren velger den representasjonen som er mest kjent for elevene.
I den siste oppgaven kan elevene bruke svaret fra 12 · 150 til å regne ut 12 · 149. Både posene, rutenettet eller areal kan brukes til å illustrere oppgaven. Læreren velger den representasjonen som er mest kjent for elevene.
Det kan være en idé å spare på notatet slik at det kan brukes senere. Elevene bør bli oppmerksomme på og reflektere over hva andre sier. Gi elevene tid til å tenke.
Mer om aktiviteten oppgavestrenger finner du på sidene til MAM-prosjektet
Matematiske sammenhenger

Hensikten med aktiviteten er at elevene skal utvikle hensiktsmessige strategier i arbeid med multiplikasjon. Mer spesielt, oppgavestrengen fremhever bruk av distributiv egenskap som en strategi i arbeid med multiplikasjon, 12 · 150 = (2 + 10) · 150 = 2 · 150 + 10 · 150 og 12 · 149 = 12 · (150 – 1) = 12 · 150 – 12 · 1. Et av målene med aktiviteten er at den gitte strategien skal begrunnes på de gitte eksemplene. Ulike representasjoner av tall og regneoperasjoner vil være nødvendige i denne sammenhengen.
Vurdering av tall og valg av hensiktsmessig strategi
Denne oppgavestrengen bygger på at elevene kan se et tall på ulike måter. For eksempel kan tallet 149 betraktes som 140 + 9, 100 + 49 osv. Denne oppgavestrengen oppfordrer elevene til å se 149 som 150 – 1. Dette gir mulighet til å regne med 150 som er et «snillere» tall. Å vurdere en multiplikasjon med tanke på å finne «snillere» tall å regne med, vil kunne forenkle regneprosessen i mange tilfeller. Kunnskap om egenskaper ved de involverte tallene og regneoperasjonen i et gitt regnestykke, gjør elevene i stand til å velge strategier som både er effektive og nøyaktige.
Ulike representasjoner av multiplikasjon og overganger mellom dem
Målet med samtalen er strategien der man ser en av faktorene som en sum eller en differanse. Begge leddene multipliseres med den andre faktoren før man adderer eller subtraherer. Strategien bør beskrives muntlig, med matematiske symboler og med en illustrasjon eller en regnefortelling. Når man skal begrunne hvorfor strategien er en gyldig framgangsmåte, er det nødvendig å gi mening til multiplikasjon gjennom en regnefortelling eller en illustrasjon (se illustrasjoner under beskrivelse av opplegget). Her kan man se multiplikasjon som like grupper, eller som antall ruter i et rutenett, eller som areal av et rektangel.
Det er viktig å være oppmerksom på at de ulike representasjonene av strategien kobles sammen, at man følger det som skjer både symbolsk, muntlig og gjennom illustrasjonen eller regnefortellingen.
Distributiv egenskap (a ± b) · c = a · c ± b · c og a· (b± c) = a · b ± a · c
Den distributive egenskap kan brukes til å regne ut alle oppgavene i denne oppgavestrengen, 2 · 150 = 2 · (100 + 50) = 2 · 100 + 2 · 50, 10 · 150 = 10 · (100 + 50) = 10 · 100 + 10 · 50, 12 · 150 = (10 + 2) · 150 = 10 · 150 + 2 · 150 og 12 · 149 = 12 · 150 – 12 · 1 = 12 · (150 – 1).
Begrunne strategien på de gitte regnestykkene 
Man kan modellere den distributive egenskapen ved å tegne rutenett eller poser med «kuler». 12 · 150 kan modelleres med 10 + 2 poser med 150 «kuler», eller rutenettet deles inn slik at den distributive egenskapen blir synlig. 12 · 149 kan skrives som 12 · (150 – 1). I en modell kan dette illustreres med at man tar bort en «kule» fra hver pose eller at rutenettet blir en kolonne kortere. Det er viktig å kombinere modellen med muntlig språk og symbolsk notasjon, slik at elevene forstår de regneoperasjonene de utfører.
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 4. trinn
- utforske og forklare samanhengar mellom dei fire rekneartane og bruke samanhengane formålstenleg i utrekningar
- Kompetansemål etter 5. trinn
- utvikle og bruke ulike strategiar for rekning med positive tal og brøk og forklare tenkjemåtane sine
- Kompetansemål etter 8. trinn
- utvikle og kommunisere strategiar for hovudrekning i utrekningar
- Kompetansemål etter 9.trinn
- beskrive, forklare og presentere strukturar og utviklingar i geometriske mønster og i talmønster
