Tårn av terninger

Opplegget er hentet fra heftet Undersøkende matematikkundervisning i videregående skole II.
Emne
Mønster, figurtall, følger, rekker, regresjon
Hensikt
Elevene skal lete etter mønster og beskrive dem matematisk ved å generalisere. De blir også introdusert for regresjon.
Du trenger
Terninger (eller centikuber) og vertikale tavler (for eksempel selvheftende whiteboardfilm).
Aktiviteten
Opplegget er tilpasset elever i den videregående skolen, men kan også passe for elever på ungdomstrinnet (med noen tilpasninger).
Elevene arbeider grupper på to eller tre. De skal undersøke tårn av terninger og beskrive de matematiske sammenhengene. I aktivitet 1 og 2 arbeider elevene på vertikale tavler, og i aktivitet 3 arbeider de i GeoGebra.
Pass på at alle elevene bygger tårnene på samme måte i aktivitet 1 og 2 slik at klassen kan sammenligne beskrivelsene i helklassesamtaler.
Aktivitet 1
Elevene bygger tårn ved å sette terninger oppå hverandre, én og én (tittelbildet til aktiviteten viser hvordan). De skal undersøke hvor mange synlige sider hvert tårn har. Deretter beskriver de sammenhengen mellom antall terninger og antall synlig sider matematisk. Til slutt deler elevene løsningene sine i helklasse.
Kommentar til læreren
Elevene arbeider på vertikale tavler. Når en gruppe har funnet antall synlige sider for flere tårn med terninger, kan læreren stille spørsmål som leder elevenes tanker mot det generelle. For eksempel «Hva om dere skal bygge et tårn med 10 terninger?» eller «Kan dere forutse hvor mange synlige sider et hvilket som helst tårn får?».
Elevene vil ofte starte med å beskrive mønsteret ved hjelp av tegning, tekst eller tabell. Så vil de oppdage at økning fra et tårn til tårnet som har en terning mer er lik, altså den rekursive sammenhengen. For eksempel at antall synlige sider øker med fire eller at tn = tn-1 + 4 t hvis t er antall synlige sider. Strategien fungerer fint så lenge elevene arbeider med påfølgende tårn, for eksempel tårn 1 og 2.
Når elevene skal finne antall synlige sider til ikke-påfølgende tårn, blir strategien mer arbeidskrevende. De fleste vil da begynne å lete etter en eksplisitt formel som ikke er avhengig av at de vet antall synlige sider til det forrige tårnet, kun hvilket nummer tårnet har. Formlene vil se annerledes ut for ulike elevpar, avhengig av hvordan de beskriver mønsteret. Derfor er det viktig med en helklassesamtale hvor elevene deler løsningene sine og argumenterer for dem. Bruk god tid og sørg for at elevene forstår hverandres løsninger.
Løsninger som inneholder feil, er gode utgangspunkt for læring. Diskuter hvorfor og gjør om slik at dem blir riktige. Omskriv gjerne alle de riktige løsningene til det samme uttrykket for å vise at de er like.
Eksempler på eksplisitte sammenhenger/formler:
«Jeg ser fire sider på alle terningene pluss én side på toppen»: 4t + 1
«Jeg ser fem sider på den øverste terningen og fire sider på de andre terningene»: 5 + 4(t – 1)
«Alle terningene har seks sider. Siden jeg ikke ser sidene mellom terningene, må jeg trekke fra to sider for hvert mellomrom. Det er ett mellomrom mindre enn antall terninger. I tillegg ser jeg ikke siden mot bordet»: 6t - 2(t – 1)-1
Aktivitet 2
Elevene undersøker hvor mange ikke-synlige sider hvert tårn har. Deretter beskriver de sammenhengen mellom antall terninger og antall ikke-synlig sider matematisk. Til slutt deler elevene løsningene sine i helklasse.
Kommentar til læreren
Hvis mulig, gi elevene en ny tavle å skrive på, slik at de kan beholde notatene fra aktivitet 1.
Eksempler på eksplisitte sammenhenger/formler:
«Det er et mellomrom mindre enn antall terninger. Hvert mellomrom har to ikke-synlige sider. I tillegg må jeg legge til siden mot bordet.»: 2(t – 1) + 1
«Det er en ikke-synlig side ned mot bordet. For hver ny terning får jeg to nye ikke-synlige sider.»: 1 + 2(t – 1)
«Hver terning har seks sider som enten er synlig eller ikke. Da må antall ikke-synlige sider være det samme som antall sider totalt minus antall synlige sider.»: 6t - 4(t + 1)
Hvis elevene summerer antall synlige og antall ikke-synlige sider får de det totale antall sider på terningene. Det er logisk ettersom en side enten må være synlig eller ikke.
Aktivitet 3
Elevene bygger tårn med terninger etter selvvalgt mønster. De bruker regresjon i GeoGebra til å finne en formel for sammenhengen mellom antall terninger i tårnet og antall synlige/ikke-synlige sider.
Kommentar til læreren
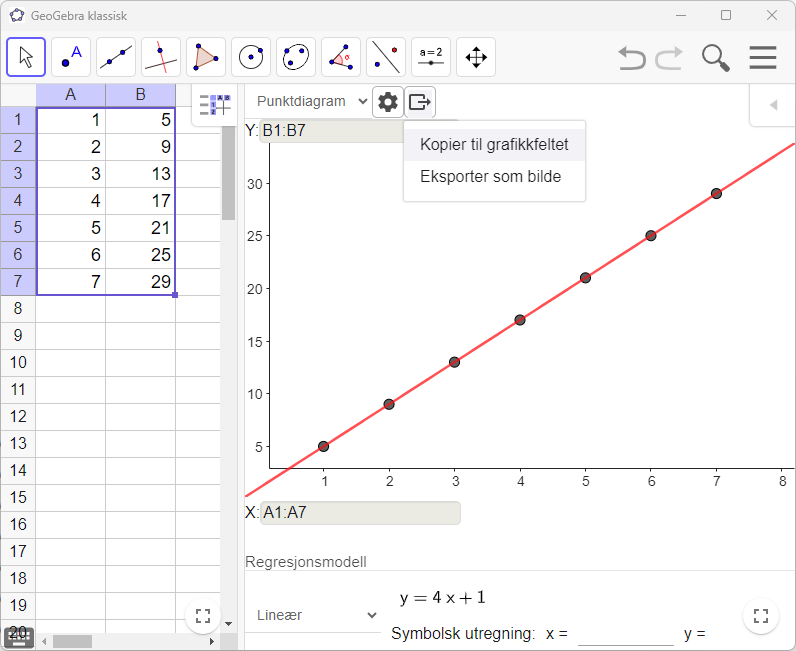
Mange elever synes det er vanskelig å finne eksplisitte formler. Regresjon med GeoGebra kan hjelpe elevene med å finne en formel basert på observasjonene de har gjort av antall terninger/tårn-nummer og antall synlige/ikke-synlige sider. Først legger elevene inn observasjonene sine i regnearket, markerer verdiene og velger Regresjonsanalyse. GeoGebra tegner da opp verdiene som punkter. Vanligvis er x antall terninger og y er antall synlige/ikke-synlige sider. Så finner elevene regresjonsmodellen som passer best til punktene.
Bruk tid på å diskutere sammenhengen mellom uttrykk og mønster. Kan de beskrive mønsteret ved hjelp av uttrykket?
Hvis elevene gjør regresjon med observasjonene fra aktivitet 1 og 2, vil modellen stemme overens med (forenklet versjon av) utrykkene de fant i aktivitet 1 og 2. Ved å kopiere regresjonen til Grafikkfeltet, kan de arbeide videre med den som en funksjon (se figur 1).
Oppsummering
Erfaringer med varierte representasjoner kan bidra til dybdelæring. I dette opplegget arbeider elevene med konkreter (terninger) og de kan bruke ulike matematiske representasjoner som tegning, ord, tabell, formel og graf. I oppsummeringen kan det være fint å diskutere sammenhengen mellom de ulike representasjonene.
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 8. trinn
- utforske, forklare og samanlikne funksjonar knytte til praktiske situasjonar
- representere funksjonar på ulike måtar og vise samanhengar mellom representasjonane
- lage og forklare rekneuttrykk med tal, variablar og konstantar knytte til praktiske situasjonar
- beskrive og generalisere mønster med eigne ord og algebraisk
- Kompetansemål etter 9.trinn
- utforske og argumentere for korleis det å endre føresetnader i geometriske problemstillingar påverkar løysingar
- beskrive, forklare og presentere strukturar og utviklingar i geometriske mønster og i talmønster
- Kompetansemål etter 10. trinn
- modellere situasjonar knytte til reelle datasett, presentere resultata og argumentere for at modellane er gyldige
- bruke funksjonar i modellering og argumentere for framgangsmåtar og resultat
- Videregående
- S1
- uttrykke egne resonnementer ved hjelp av matematiske begreper og symbolspråk
- Vg1P
- bruke digitale verktøy i utforsking og problemløysing knytt til eigenskapar ved funksjonar, og diskutere løysingane
- identifisere variable storleikar i ulike situasjonar og bruke dei til utforsking og generalisering
- modellere situasjonar knytte til tema frå samfunnsliv og arbeidsliv, presentere og argumentere for resultata og for når modellane er gyldige
- tolke og bruke funksjonar i matematisk modellering og problemløysing
- Vg1T
- formulere og løyse problem ved hjelp av algoritmisk tenking, ulike problemløysingsstrategiar, digitale verktøy og programmering
- identifisere variable storleikar i ulike situasjonar, setje opp formlar og utforske desse ved hjelp av digitale verktøy
- modellere situasjonar knytte til ulike tema, drøftedrøfte, presentere og forklare resultata og argumentere for om modellane er gyldige
