Puslespill med Pytagoras setning
Emne
Pytagoras setning, bevis
Hensikt
Å forstå et visuelt bevis for Pytagoras setning og å kunne gjennomføre et bevis.
Du trenger
Aktiviteten
La elevene arbeide i par. De skal diskutere, reflektere og konkludere, og de skal skrive ned det de kommer fram til. Elevene kan ha løst oppgavene og skrevet løsninger på ulike måter. La dem få presentere de ulike løsningene, det kan være utgangspunkt for en samtale som kan gi bedre forståelse.
Opplegget er laget for å illustrere Pytagoras’ setning. Det kan utvides ved at dere ser på hva som mangler for at dette skal være et bevis for setningen. Så kan man utvide med det som trengs for å bevise setningen med utgangspunkt i puslespillet.
Oppgave til elevene
Klipp ut puslespillet i vedlegget slik at du får fem biter.
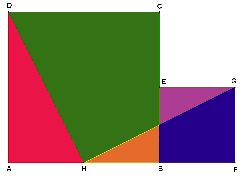
Vi har to kvadrater slik som vist på figuren nedenfor. Sidelengden til det lille kvadratet BFGE er halvparten av sidelengden i det store kvadratet ABCD. Punktet H ligger midt på sida AB.
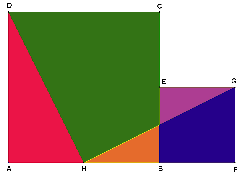
a) Sammenlign trekantene AHD og FGH. Hva har disse to trekantene felles?
b) Hva er arealene til de to kvadratene uttrykt ved sider i trekantene?
c) Vis at bitene kan settes sammen til et stort kvadrat.
d) Uttrykk arealet av dette kvadratet ved hjelp av sider i trekantene.
e) Forklar at dette puslespillet viser Pytagoras’ setning.
Rammeplanmål/Kompetansemål
- Videregående
- S1
- uttrykke egne resonnementer ved hjelp av matematiske begreper og symbolspråk
- Vg1P
- modellere situasjonar knytte til tema frå samfunnsliv og arbeidsliv, presentere og argumentere for resultata og for når modellane er gyldige
- tolke og rekne med rotuttrykk, potensar og tal på standardform
- Vg1T
- utforske samanhengar mellom andregradslikningar og andregradsulikskapar, andregradsfunksjonar og kvadratsetningane og bruke samanhengane i problemløysing
- Vg2P
- utforske og forklare korleis formlikskap, målestokk og eigenskapar ved geometriske figurar kan brukast i berekningar og i praktisk arbeid
