Sannsynlighet - Venndiagram

Dette opplegget er hentet fra heftet Undersøkende matematikkundervisning i videregående skole II.

Firkantete tellebrikker (overheadbrikker/fargete gjennomskinnelige), mengderinger eller hyssing, klistrelapper og kopioriginal.

INTRODUKSJON

Før man gjennomfører opplegget, må læreren reflektere over spørsmål som kan stilles for å stimulere elevene i arbeidet. Ikke gi elevene svar på spørsmål, men still deg undrende til problemstillingene sammen med elevene.

DIDAKTISK BEGRUNNELSE

Gjennom utforsking og en induktiv tilnærming til lærestoffet vil mange elever oppleve en ny innfallsvinkel til dette temaet. De bygger selv opp forståelse for temaet, og i samarbeid og samtale med andre elever forsterker de begrepsdannelsen. For mange elever er det læringsstøttende å jobbe med konkreter og å visualisere oppgaven de skal løse. Det er også viktig å forberede spørsmål som underbygger forståelse for temaet, slik at elevene selv finner svar på oppgaven. Oppgaven gir rom for å trekke inn flere begreper fra sannsynlighet, og det gir læreren gode muligheter for å tilrettelegge for den enkelte elevs læring.

OPPLEGG 1: VENNDIAGRAM                                            

AKTIVITET 1

Denne oppgaven gjøres i fellesskap. Målet er å vise oppbyggingen av venndiagram.

I starten av timen må læreren skrive følgende oppgave på tavlen:

I en klasse er det 29 elever. Når vi undersøker idrettsinteressen finner vi at 18 elever i klassen liker fotball, og 13 elever liker ski. 5 av elevene liker ingen av disse to idrettene.

Mange elever vil si at læreren har gjort en feil, da 18 + 13 + 5 er mer enn 29. Dermed er klassesamtalen i gang, og man kan utfordre elevene til å systematisere opplysningene.

Eleven får firkantbrikker og jobber parvis med systematiseringen.

• Velg først ut 29 blå brikker som illustrerer antall elever i klassen. Deretter tar du 18 grønne
  
  brikker som illustrerer det «å like fotball», og 13 røde brikker som illustrerer det «å like ski»
• Legg ut de 29 blå elev-brikkene på bordet.
• Skyv 5 blå elev-brikker litt for seg selv. Dette illustrerer de elevene som ikke liker noen av de to idrettene vi jobber med.
• Plasser brikkene med egenskapene «å like fotball» og «å like ski» oppå de blå elevbrikkene.
• Alle egenskapene må få plass.

Med brikkene foran seg og på elektronisk tavle eller overhead, kan læreren stille følgende spørsmål til

klassen. Læreren noterer svarene på tavlen.

Hvor mange av de 29 elevene

• Liker ikke noen av idrettene.

• Liker kun fotball.

• Liker kun ski.

• Liker både fotball og ski.

• Summer de fire svarene. Kan dere gi en begrunnelse for summen?

Kommentar til læreren

Elevene har nå funnet frem 29 brikker som illustrerer elevene i klassen. Av disse er det 5 elev-brikker som ikke skal ha noen egenskap, og de legges litt for seg selv. Det er da igjen 24 elev-brikker som skal gis egenskap. Av egenskaper har vi 18 som liker fotball og 13 som liker ski, altså har vi 31 egenskaper som skal plasseres totalt. Det betyr at det må være noen elever som liker både fotball og ski, og som derfor skal tillegges to egenskaper. Legg også merke til ordbruken i oppgaven. Det står at 18 elever liker fotball, det står ikke at 18 elever liker kun fotball. Dette er det fint om læreren påpeker overfor elevene, for da stimulerer læreren elevene til å diskutere hvordan de kan ha 31 egenskap-brikker, når

det kun er 24 elev-brikker som skal ha egenskap.

I store klasser vil det ikke være mulig at alle elever velger de samme fargene som blir anbefalt i teksten.

Da er det viktig at elevgruppene noterer hva den enkelte fargen står for.

Figuren nedenfor illustrerer hvordan elevene kan ha lagt brikkene. Her er røde og grønne brikker lagt oppå de blå, og det er 7 blå brikker med både en rød og en blå oppå.

AKTIVITET 2

Elevene jobber videre med brikkene. Oppgavene gis muntlig. Gi elevene nok tid til å utføre oppgaven.

Oppgave:

• Ta to mengderinger, ev. løkker av hyssing. På den ene ringen settes en klistrelapp med «liker fotball» og på den andre en klistrelapp med «liker ski».
• Plasser brikkene fra den forrige oppgaven slik at alle elevbrikkene får sin plass.
• Tenk over hvordan dere må legge ringene slik at dere kan plassere alle brikkene. Kravet er at det bare skal være brikker med én egenskap i hver mengde, dvs. i hvert «rom».
• Hvor mange brikker/elever er det i hvert rom?

Kommentar til læreren

Elevene skal nå bruke funnene fra forrige oppgave til å legge ringene. Elevene utfordres til å finne ut hvordan de skal plassere ringene slik at de får et «rom» som inneholder begge egenskapene, dvs. både fotball og ski. Poenget er at man får avgrenset mengdene slik at alle brikkene i hvert «rom»/mengde har samme egenskap.

Denne delen av oppgaven oppleves erfaringsmessig som vanskelig for elevene når de gjør den kun ved regning. Å ha oppgaven konkretisert vil kunne hjelpe for å forstå oppgaven. Elevene vil kunne erfare at når samme person liker to idretter, så må det dannes et overlappende område mellom de to mengderingene. Når elevene har lagt ferdig brikkene, vil det ligge 11 blå/grønne, 7 blå/grønne/røde, 6 blå/røde og 5 blå brikker på bordet. Læreren bør vie dette punktet stor oppmerksomhet, og han må legge til rette for en god faglig dialog.

Her kan man ta opp spørsmålene fra aktivitet 1. Nå skal det være lettere å finne svaret, da brikkene er sortert i enkelte mengder/«rom».

AKTIVITET 3

Oppgaveark 1: Venndiagram 1

Elevene jobber i par med hvert sitt oppgaveark.

Når elevene har forstått oppbygningen av venndiagrammmet, er det viktig at de får øve seg.

Oppgavearket er bygd opp slik at de første oppgavene er enkle å gjøre med brikker, mens elevene må finne tallene uten konkreter i de siste oppgavene. Denne tenkingen viser veien til det som i neste opplegg blir forklart som «addisjonssetningen».



Kommentar til læreren

Når vi bruker venndiagram i matematikken, må man merke seg at det skal være en ytre ramme i tillegg til mengdesirklene. Også de 5 brikkene skal plasseres innenfor den ytre rammen. Hver brikke-stabel representerer et utfall, og mengden av alle brikkene utgjør utfallsrommet. Det er alltid viktig å skaffe seg oversikt over hele utfallsrommet når man arbeider med problemer i sannsynlighetsregning.



Her introduseres skrivemåten med symboler. Det er viktig at elevene lærer seg de formelle kravene.

For å bruke skrivemåten med symboler i sannsynlighetsregning, bør man lage forkortelser for alle kategorier (hendinger). Krev at elevene skriver hva de enkelte forkortelsene står for i hver ny oppgave. I oppgave 1 kan elevene skrive cola og solo på de to mengdesirklene, men hvis de vil bruke forkortelser, skal de skrive:

C : (en tilfeldig valgt elev) liker cola

S : (en tilfeldig valgt elev) liker solo

I tillegg til antall i hver mengde (hvert rom), skal det også skrives totalt antall på rammen rundt (hele utfallsrommet).

Fasit og merknader for oppgavene:

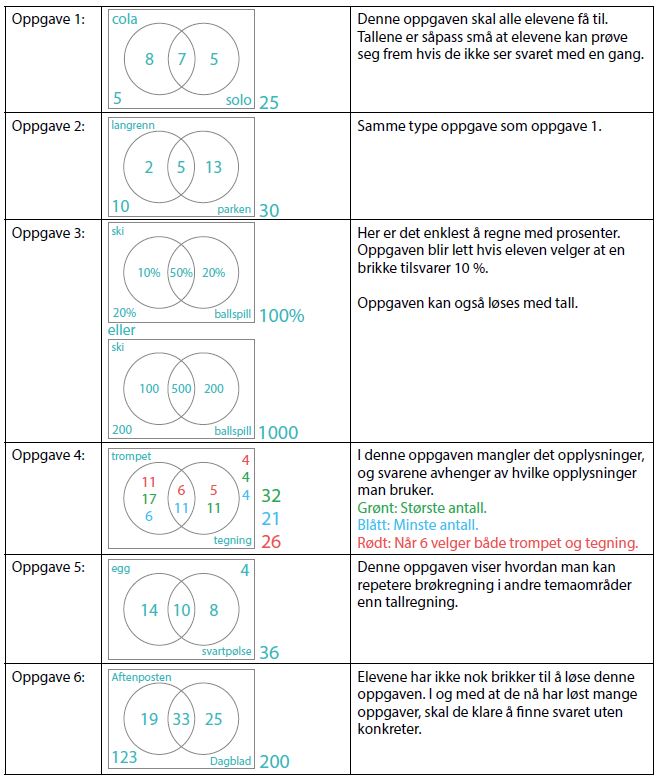
AKTIVITET 4

Oppgaveark 2: Venndiagram 2

Vi går tilbake til utgangspunktet fra aktivitet 1:

I en klasse er det 29 elever. Når vi undersøker idrettsinteressen finner vi at 18 elever i klassen liker fotball, og 13 elever liker ski. 5 av elevene liker ingen av disse to idrettene.



For å få en god overgang til sannsynlighetsregning, innfører vi skrivemåten P(...) for «sannsynligheten for…» og en del symboler.



Forkortelsene må forklares:



F : (en tilfeldig valgt elev) liker fotball

S : (en tilfeldig valgt elev) liker ski

∪ : union betyr «enten det ene eller det andre eller begge deler» (liker enten ski eller fotball eller begge deler).

      Ofte sier vi bare «eller»

∩ : snitt betyr «og samtidig» eller «både – og» (liker både fotball og ski). Ofte sier vi bare «og»

Strek over symbolet betyr «ikke» (liker ikke fotball)

F \ S : Skrå strek betyr «uten» eller «men ikke» (liker fotball, men ikke ski)

Oppgave 1

Fargelegg de ulike mengdene i Venndiagrammene nedenfor:

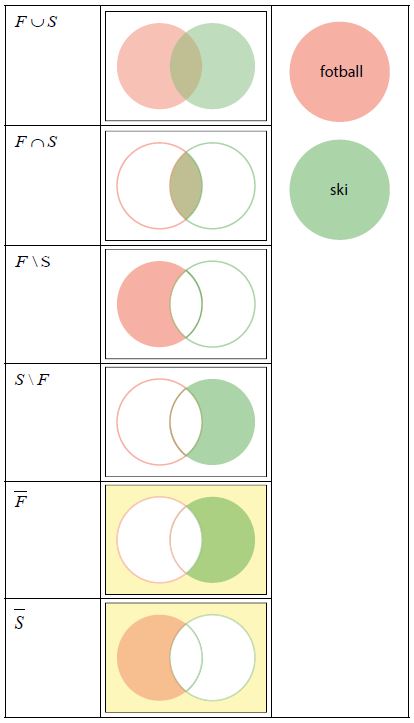
Nå bruker vi det vi har lært til å regne sannsynligheter.

Oppgave 2



Oversett til symbolspråk og regn ut følgende sannsynligheter:

• Sannsynligheten for at en elev liker fotball.

• Sannsynligheten for at en elev liker ski.

• Sannsynligheten for at en elev ikke liker noen av idrettene.

• Sannsynligheten for at en elev liker både fotball og ski.

• Sannsynligheten for at en elev liker ski eller fotball.

• Sannsynligheten for at en elev kun liker ski.

Kommentar til læreren

De fire nye symbolene kan illustreres med skisser der man fargelegger de aktuelle mengdene. La elevene foreslå hvilken mengde som skal fargelegges i hvert av tilfellene.

Bruk god tid på å oversette fra tekst til symboler, og sørg for at symbolene alltid oversettes til ord når de leses.

P(F) leses som «sannsynligheten for at en (tilfeldig valgt) elev liker fotball». (P står for probability.)

Sannsynlighetene er forhold mellom to tall. Det er viktig å vite hva man skal dele på, dvs. hva som er «det hele» eller utfallsmengden. I alle disse eksemplene finner vi hvor stor del de enkelte delmengdene utgjør av antall elever i hele klassen.

Elevene har antakelig lært at sannsynligheter kan skrives både som brøk, desimaltall og prosent på ungdomsskolen. Dette er en fin anledning til å se sammenhengen mellom de tre ulike måtene å skrive samme tall på. Spesielt for elevene på 1T er det viktig at læreren understreker at brøksvaret er et eksakt svar, mens desimaltall og prosent er et mer eller mindre nøyaktig svar.

UTVIDELSE AV OPPGAVEN

Tre mengderinger gir flere valgmuligheter. For å jobbe med begrepene «union» og «snitt», kan det være en mulighet å skravere de ønskete områdene uten å bruke tall.

I en gruppe personer leser noen Dagbladet, noen Morgenbladet og noen Aftenposten.

• Marker området for alle personer som leser nøyaktig to aviser.
• Marker området for alle personer som leser Dagbladet og Morgenbladet.
• Marker området for alle personer som leser Aftenposten eller Dagbladet, men ikke Morgenbladet.
• Osv.

OPPLEGG 2: ADDISJONSSETNINGEN

I dette opplegget skal elevene få en forståelse for addisjonssetningen ved hjelp av venndiagram.



Elevene jobber i par med oppgaveark.

Oppgave 1

En gruppe med 20 personer ble spurt om de har søsken. 12 svarte at de har brødre, 10 at de har søstre, mens 6 personer er enebarn.

• Legg informasjonen med brikker inn i et venndiagram. Sett navn på mengdene. Skriv antallene inn i venndiagrammet.
  
  » Bruk forkortelsene
  
  » B: har brødre
  
  » S: har søstre
• Finn sannsynlighetene

Oppgave 2

Addisjonssetningen i sannsynlighet er gitt ved formelen:

P(A ∪ B) = P(A) + P(B) − P(A ∩ B)

• Skriv setningen slik at den passer til oppgave 1 ovenfor.
• Forklar det som står i formelen med ord.

Oppgave 3

I en skoleklasse på 28 elever ble det gjort en undersøkelse for å finne ut hvem som hadde vært i Tyskland og hvem som hadde vært i Frankrike. Det viste seg at 13 elever hadde vært i Tyskland, 15 hadde vært i Frankrike, mens 4 ikke hadde vært i noen av disse landene.

• Skriv opp forkortelsene du vil bruke.
• Tegn opplysningene inn i venndiagrammet.
• Bruk addisjonssetningen og finn sannsynligheten for at en elev i denne klassen har vært i Tyskland eller Frankrike.

Oppgave 4

En gruppe på 25 elever blir spurt om de går på ungdomsskolen eller på videregående skole. 15 elever svarer

at de går på ungdomsskolen, 8 elever svarer at de går på videregående skole, og 2 elever svarer at de ikke

går på skole.

• Tegn opplysningene inn i venndiagrammet.
• Skriv opp forkortelsene du vil bruke.
• Bruk addisjonssetningen og finn sannsynligheten for at en elev går på videregående skole eller på ungdomsskolen.
• Hvorfor er denne oppgaven mye enklere enn oppgave 2?

Kommentar til læreren

Prøv å få elevene til å se og forklare hvorfor formelen stemmer med venndiagrammet. Se spesielt på hvorfor man må trekke fra sannsynligheten for snittmengden for å finne sannsynligheten for unionen.

Det er viktig å problematisere ordet «eller».

Pass på at elevene leser forkortelsene med fulle setninger.

OPPSUMMERING

Til slutt må man se tilbake og få et overblikk over hva man har arbeidet med og lært gjennom klassesamtale. Bruk elevenes arbeider med konkretene som innfallsvinkel til oppsummering. Ta utgangspunkt i venndiagrammet, og la elevene beskrive funnene de har gjort, og hvordan de har jobbet med oppgaven. Se spesielt på overgangen fra venndiagrammet til sannsynlighetsregning. Løft gjerne frem noe av det elevene har skrevet for å synliggjøre at det er viktig at de dokumenterer arbeidet sitt. Opplegget viser hvordan man kan jobbe med mer kompliserte oppgaver uten å bruke faguttrykkene i undersøkelsesfasen, men heller bygge opp disse etter hvert. Hovedfokuset er rettet mot forståelse for temaet, for deretter å formalisere det med faguttrykk og formler.