Telle med 4 fra 4

Beskrive, bruke og begrunne mønstre og sammenhenger.

Dette opplegget er utviklet som en del av prosjektet Mestre ambisiøs matematikkundervisning.

Tavle, gjerne interaktiv tavle, eller flippover.

Start tellingen på fire og tell med 4 om gangen. Skriv tallene i kolonner på fem. Det kan være til hjelp å lage et tomt rutenett på forhånd. Skriv tallet 4 og gi elevene tid til å tenke ut de neste tallene. Elevene sier tallene i kor samtidig som læreren skriver tallet. Tabellen fylles ut under tellingen, og elevene beskriver hvordan de bruker mønstre og sammenhenger til å finne tallene. Noter elevenes forslag og marker mønstre og sammenhenger i tabellen. Det kan være en idé å spare tabellen med notater slik at den kan brukes igjen senere.

De matematiske sammenhengene i opplegget «telle med 4 fra 4» blir drøftet nærmere nedenfor.

Elevene bør bli oppmerksomme på, og reflekterer over hva andre sier. Gi elevene tid til å tenke.

Mer om Telle-i-kor-aktiviteter finner du her. 

Matematiske sammenhenger

Mønster på ener og tierplass

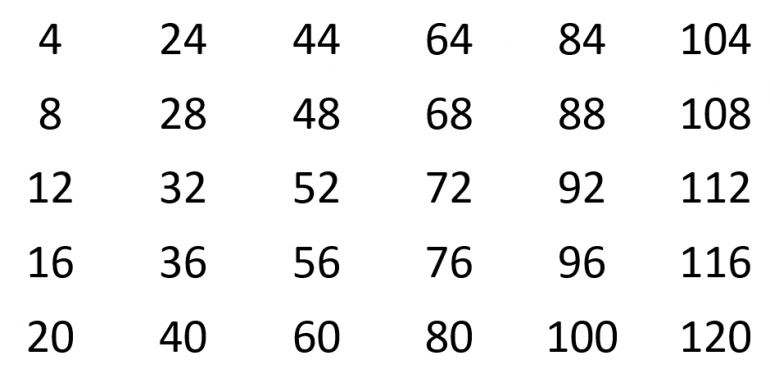
Tellingen starter på 4 og øker med 4. I hver rad har tallene samme siffer på enerplassen. Fra kolonne til kolonne øker tierne med to. Den matematiske begrunnelsen for denne økningen er at fire adderes fem ganger i hver kolonne, 5 ∙ 4 = 20. Denne relasjonen mellom tall gjelder ikke bare mellom tallene i nederste rad. Den gjelder med samme begrunnelse for alle radene.

Fra og med kolonne seks ser man at tallene på tierplassen og enerplassen gjentar seg, noe som kan forklares ut fra at 4 · 5 · 5 = 100.

Diagonaler i tabellen

Mønster som kommer fram ved å betrakte diagonaler i tabellen, kan også gi noen matematiske utfordringer. Enerplassen i hver kolonne følger mønsteret 4 – 8 – 2 – 6 – 0, og det samme mønsteret finner man også på enerplassen hvis man følger tallene i tabellen på skrå nedover, for eksempel fra 24 – 48 – 72 – 96 – 120. Dette kan forklares matematisk ved at man ser på differansen mellom tallene på skrå nedover som er 6 ∙ 4  = 24. Slike betraktninger kan gi gode matematiske diskusjoner og inspirere elever til å lete etter nye sammenhenger i en relativt enkel tabell.

4-gangen og distributiv egenskap

Tabellen er også en multiplikasjonstabell for 4-gangen. Det gjør det mulig å kombinere tall direkte for å finne nye tall i tabellen. Dersom dette er et mål for aktiviteten, still gjerne spørsmål som leder elevene mot det å se etter sammenhenger mellom tall i tabellen, og hvordan det er mulig å bruke tallenes plassering i tabellen til å finne nye tall som kommer. Å se på sammenhengen mellom tallenes plassering og verdien av tallene, kan også brukes til å forklare og forstå hvordan tall kan deles opp og uttrykkes på ulike måter.

Tallet i rute 5 + Tallet i rute 8  = Tallet i rute 13   

          20           +          32           =          52

        5 · 4          +         8 · 4         =         13 · 4

Her er det også mulig å gå inn på distributiv tenking, for eksempel:  13 ·  4 = (5 + 8) · 4 =  5 · 4 + 8 · 4

Tilsvarende kan man også behandle subtraksjon.

Med en slik tabell som utgangspunkt vil elevene nokså sikkert finne flere lignende eksempler som kan brukes som et utgangspunkt for å forklare distributivitet dersom dette er et av målene for aktiviteten.

Egenskaper ved partall

I telling med 4 kan man diskutere egenskaper ved partall. Ved å innføre en variabel n, kan man få en mer algebraisk tilnærming til tallenes plassering og verdi i tabellen. Partall er på formen 2 · n, der n er et naturlig tall.  Når man teller med fire, vil alle tallene være på formen 2 · 2 · n. Man får altså annethvert partall i tellingen. Det kan være interessant å se på hvilke partall som ikke er i tabellen og hva som skiller dem fra de man finner i tabellen.

Partall som ikke er i tabellen kan uttrykkes algebraisk på formen 2 ∙ 2 ∙ n - 2.

En mulig utvidelse i denne tellingen, gjerne på et senere tidspunkt, kan være å se videre på egenskapene til partallene som er i 4-gangen og i 8-gangen. Å halvere partall gjentatte ganger kan være et utgangspunkt for å se hva som skiller tallene i 4-gangen fra de tallene som også finnes i 8-gangen.