1 time
Par

Kvadrat + kvadrat = kvadrat

Kvadrat + kvadrat

Emne

Dynamisk geometri, rettvinklet trekant, Pytagoras’ setning

Hensikt

Elevene skal få dypere forståelse for Pytagoras’ setning ved å arbeide med kvadratene på sidene i en rettvinklet trekant.

Valg av tidspunkt

Når elevene har arbeidet en stund med Pytagoras’ setning eller som en repetisjon.

Du trenger

PC med GeoGebra

Aktiviteten

Oppgave til elevene:

  • Tegn to kvadrater med tydelig forskjellig størrelse. Gi dem forskjellig farge og vis arealene.
  • Tegn et nytt, dynamisk kvadrat med areal lik summen av arealene til de to kvadratene.
  • Dra i de to start-kvadratene for å se om sammenhengen alltid stemmer.

Kommentar til læreren

Start med en klassesamtale om hva elevene tenker på når de hører «Pytagoras’ setning».

Vanlige elevsvar:

  • a2 + b2 = c2
  • kat2 + kat2 = hyp2
  • katet2 + katet2 = hypotenus2
  • Rettvinklet trekant
  • Hypotenus
  • Katet

Mange elever tenker på «Pytagoras’ setning» kun som en algebraisk formel. Utfordre elevene til å forklare sammenhengen geometrisk. Sørg for at elevene forstår at a2, b2 og c2 er kvadrater. Pytagoras’ setning sier da at summen av arealene til kvadratene på katetene er lik arealet til kvadratet på hypotenusen. I opplegget skal de bruke denne sammenhengen i GeoGebra.

Be elevene åpne GeoGebra og gi så oppgaven muntlig. Vis den gjerne på storskjerm også. Elevene arbeider i par slik at de kan diskutere underveis. Alle bruker hver sin PC med GeoGebra. Sørg for at elevene tar bort koordinatsystem og rutenett. I tillegg bør de også sorterte objekter etter type, ikke vise navn på nye objekt og bare bruke én desimal. Se Lær GeoGebra: GeoGebra-tips for lærere for veiledning.

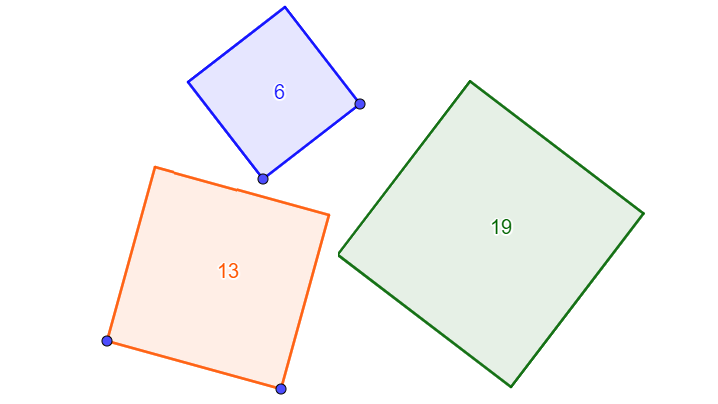
Elevene kan tegne det nye kvadratet på ulike måter, avhengig av kunnskapene deres i matematikk og i GeoGebra. Uansett hvordan de lager kvadratet skal figuren være dynamisk. Det vil si at dersom elevene endrer størrelsen på et av de to start-kvadratene så skal GeoGebra også endre størrelsen på det nye kvadratet. Tips dem gjerne om verktøyet Passer. Det gjør det lett å sette av sidelengder.

Eksempler på konstruksjon:

Løsning 1 

Løsning 2

Oppsummering

Velg ut noen elevpar som viser fram og forklarer hvordan de har kommet fram til løsningen sin. Oppfordre til å bruke matematiske begreper som katet, hypotenus, areal og kvadrat. Opplegget Kvadrat - kvadrat = kvadrat passer bra som en fortsettelse.