Hvorfor er dette riktig, og hvorfor er dette feil?

Kjerneelementene skal være bærende elementer i matematikkundervisningen, og fremhever viktige aspekter i undervisningen. Ett av kjerneelementene: resonnering og argumentasjon, er en tilnærming mot det å utvikle matematiske bevis. Hensikten er å tilrettelegge for en progresjon fra uformelle bevisføringer i begynneropplæringen, til en stadig økende grad av formelle matematiske føringer oppover i trinnene. Å argumentere kan fungere som en brobygger mellom den uformelle bevisføringen og den formelle bevisføringen.

De viktige spørsmålene

Elevene må lære hvordan de skal resonnere og argumentere for sine matematiske løsninger, det kommer ikke av seg selv. Jaworski (2010) hevder at det å undervise utforskende matematikk ikke er en metode, men en grunnleggende holdning til matematikkfaget. Det samme gjelder for resonnering og argumentasjon, når dette kjerneelementet skal finne sin naturlige plass i matematikkundervisningen. Et enkelt grep er å justere måten du stiller spørsmålene til elevene på. I stedet for å be elevene regne ut 11 – 4, kan man utfordre elevene til å vise hvorfor 11 – 4 = 7. Dersom elever i større grad utfordres med spørsmål som «Vis at ...» eller «Argumenter for at ...», vil elevene resonnere, bruke og bevise de generelle idéene om hvordan matematiske idéer fungerer (Russell, 1999). Elevene må lære å spørre seg selv «Kan dette stemme?» og «Hvorfor er dette riktig?».

Skap mulighetsrom med kenguruoppgaver

Oppgavene fra Kengurukonkurransen er problemløsningsoppgaver, med fem svaralternativer, hvor flesteparten egner seg til å jobbe med resonnering og argumentasjon. Når elever jobber med problemløsning møter de et problem de ikke kjenner til fra før, som de skal løse, og samtidig vurdere om løsningene er gyldige (LK20). Når de vurderer gyldigheten i sine løsninger kan de utfordres til å argumentere og begrunne hvorfor de mener at svaret er riktig. 

Mange kenguruoppgaver bygger på matematiske idéer, og er satt inn i kontekster for å vekke nysgjerrighet og engasjement hos elevene. Det er ikke sikkert at elevene oppdager disse idéene når de jobber med oppgavene alene. Du bør derfor benytte mulighetene som ligger i gode oppgaver, og utnytte mulighetsrommet som åpnes rett etter at elevene har jobbet med en oppgave. Om du løfter frem en «fersk» oppgave i en matematisk samtale gir det elevene flere muligheter til å oppdage den matematiske idéen. Det skaper samtidig et rom for å studere idéen grundigere fra ulike sider:

• Hva om vi gir oppgaven nye tall? Vil løsningen bli den samme?
• Kan vi løse oppgaven ved å bruke de samme strategiene? Oppstår det nye mønstre?

Resonnering og argumentasjon er nøkkelen i dette arbeidet.

Det å motbevise

Kenguruoppgavene åpner altså opp for matematiske samtaler hvor elevene kan utforske og utvikle sin matematiske argumentasjon. I de fem svaralternativene ligger det ett riktig og fire uriktige svar, og dette er noe du kan dra nytte av i undervisningen. Det mest nærliggende er å finne og argumentere for riktig løsning til en gitt oppgave. Det vil naturligvis være den sterkeste triggeren hos elevene når de løser oppgaven, men jeg vil anbefale deg å utnytte nye muligheter som svaralternativene gir. Et viktig aspekt innenfor arbeidet med matematiske bevis er nemlig det å motbevise. Dette aspektet må også vies oppmerksomhet i undervisningen, på lik linje med det å bevise.

Kenguruoppgavene inviterer til ulike måter å resonnere seg frem til riktig svaralternativ. Det å eliminere bort svaralternativer, som ikke kan være riktige, vil derfor være en effektiv strategi. En slik elimineringsstrategi rører ved det å motbevise. Det å utforske hvorfor et svaralternativ ikke kan være riktig, gir elevene muligheter til å studere den matematiske idéen fra et nytt perspektiv. Derfor vil elimineringsmetode gi elevene gode muligheter til også å argumentere mot et svaralternativ. Ved å oppmuntre elevene til å finne et svaralternativ som ikke kan være riktig, vil de samtidig utfordres til å sette ord på hvorfor. Dette vil støtte elevene når de senere utvikler matematiske argumenter for eller mot matematiske påstander.

 

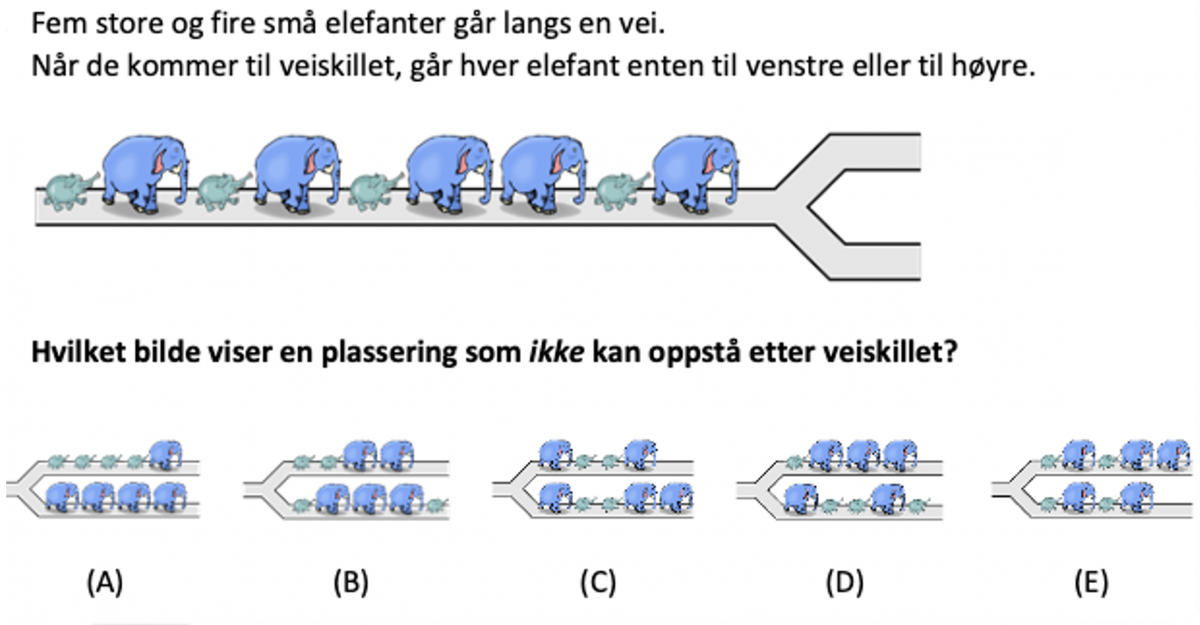
I oppgaven med de ni elefantene skal elevene finne en plassering som ikke kan oppstå etter et veiskille, med utgangspunkt i hovedbildet. Å eliminere bort svaralternativer vil være en egnet strategi, hvor resonneringen bak elimineringene vil hjelpe elevene med å forstå hvorfor C er det riktige svaralternativet. Elevene kan benytte seg av konkreter for å modellere handlingen i oppgaven, eller fysisk utføre oppgaven. Elevene kan komme fram til riktig svaralternativ, f.eks. ved prøving og feiling, uten at de nødvendigvis trenger å forstå hvorfor det må være slik. Om du følger opp med spørsmålet: «Argumenter for hvorfor svaralternativ A ikke kan være riktig», vil elevene i større grad bli utfordret til å begrunne og vise forståelse for hvorfor C må være riktig. De må sette ord på hva det er de har funnet ut, og hvorfor det stemmer matematisk. I oppgaven med elefantene vil det å bygge argumentasjon rundt plasseringen til den lille elefanten bakerst i rekken, være viktig. Å vise til at plasseringen må bety at den samme elefanten også må stå bakerst i en av de nye rekkene etter veiskillet, vil være et viktig argument i bevisføringen for hvorfor C må være det riktige svaralternativet.

Overbevis en venn

Det finnes ulike pedagogiske grep for å la resonnering og argumentasjon bli en naturlig del av matematikkundervisningen. På alle trinn kan det å overbevise en venn (Boaler & Humphreys, 2005) være et fornuftig grep. Argumentasjonen en elev gir kan være av en slik karakter at medeleven blir overbevist, og forstår hvorfor svaralternativet er det riktige. For å klare dette må eleven først ha overbevist seg selv om hvorfor det valgte svaralternativet må være det riktige. Det å overbevise en venn er et forholdsvis enkelt grep, hvor medelevene underveis kan stille oppfølgende spørsmål slik at eleven kan omformulere eller finjustere sin matematiske argumentasjon. Å bruke det å overbevise en venn over tid vil hjelpe elevene med å beherske aktiviteten, og i større grad dra nytte av argumentasjon i arbeidet mot en formell bevisføring.



 

Oppgaven om laserstrålen som reflekteres i speil har en lav inngangsterskel for å jobbe med det å overbevise en venn. Elevene må argumentere for hvordan retningen til laserstrålen vil bevege seg gjennom samlingen med speil. Det å tegne opp laserstrålens endring av retning vil støtte elevens argumenter og begrunnelsen for valg av svaralternativ.

Tegningen vil i tillegg støtte medeleven til å utfordre argumentasjonen om den ikke er overbevisende nok, eller til å danne motargumenter dersom man er uenig med resonnementet og løsningen. Når elevene begynner å beherske det å overbevise en venn, kan vennen øke motstanden i det å la seg overbevise. Økende motstand vil kreve en grundigere resonnering for å kunne danne mer presise argumenter. Slik må elevene stadig finjustere sine argumenter. I laserstråleoppgaven kan finjusteringen være at de bruker matematiske begreper i argumentasjonen. Det kan være en overgang fra å bruke fingerpeking og enkel kommunikasjon, til kun å bruke verbal forklaring med matematiske begreper. Et eksempel på formulering kan være: «Laserstrålen kommer inn fra venstre. I det første speilet blir laserstrålen speilet i 90°, og sendt oppover. I møtet med det neste speilet brytes strålen på nytt i 90°, og sendes mot venstre ...». 

Etter hvert som elevene erverver rike erfaringer med å argumentere for og mot matematiske påstander, kan elevene møte større motstand hos eleven som skal overbevises. I stedet for å overbevise en venn kan elevene utfordres til å overbevise en skeptiker (Volmink, 1990). Denne skeptikeren kan fremdeles være en medelev, som nå er mer øvd i det å argumentere matematisk. Det kan også være en lærer som er skeptikeren. Det å overbevise en skeptiker hever nivået på den matematiske argumentasjonen, både til den som argumenterer og til den som er skeptisk. Grepet gir en naturlig progresjon i arbeidet med resonnering og argumentasjon, hvor elevene i stadig større grad må finjustere sine matematiske argumenter. I et lengre progresjonsløp, med stadig sterkere krav til matematisk stringens i argumentene, kan neste steg være å overbevise en faglig sterk person eller en fagperson (Davis & Herch, 1981). Matematikklæreren eller en elev fra et høyere klassetrinn, kan ta denne rollen. 

Endre premiss i oppgavene

Et annet pedagogisk grep er å la elevene jobbe i par eller grupper på tre hvor de får tildelt hvert sitt svaralternativ. Parene eller gruppene må enes om argumenter for hvorfor svaralternativet de fikk tildelt, er det riktige eller ikke. Du kan utfordre de elevene som har uriktige svaralternativer, til å argumentere for hvilke premisser i oppgaven som må endres slik at deres svaralternativ vil bli det riktige. I det forrige eksempelet (laserstrålen), kan premissendringene være å endre vinkel på speilflater slik at laserstrålen treffer deres svaralternativ. Elevene kan videre utfordres til å gjøre så få endringer som mulig, og argumentere for at det ikke kan gjøres færre endringer enn det de har kommet frem til. 

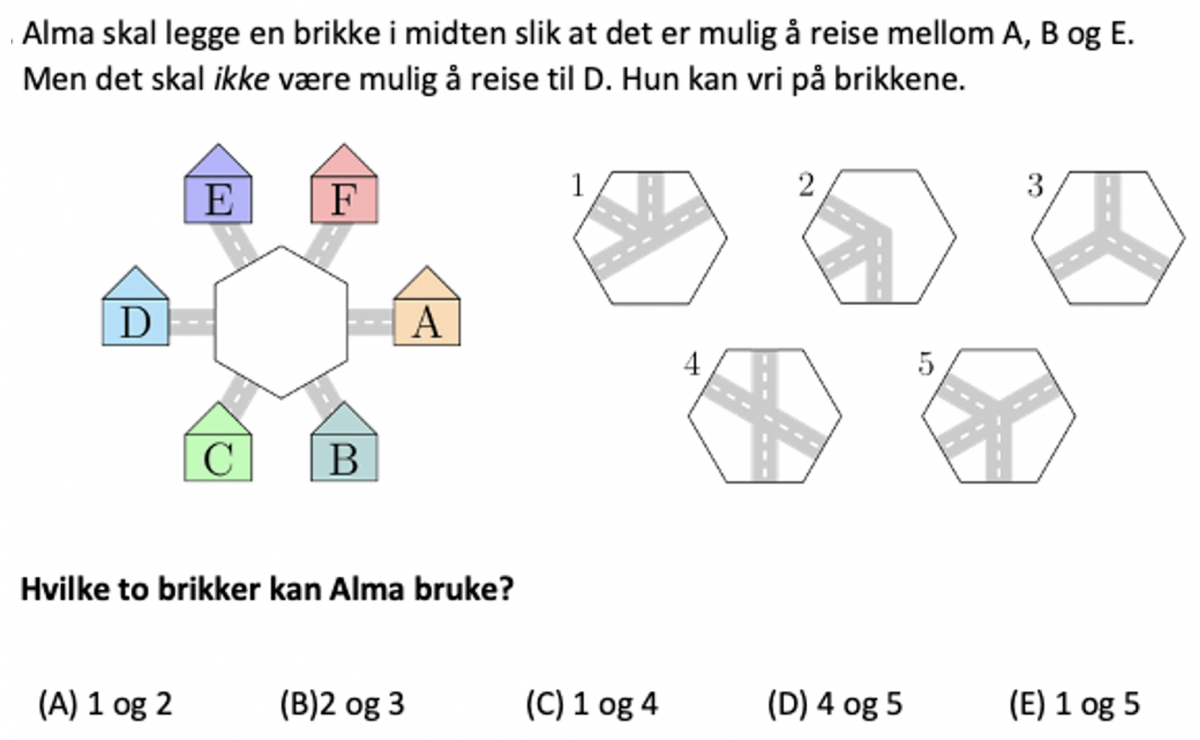
I denne oppgaven skal elevene finne de to brikkene som Alma kan legge slik at premissene oppfylles. I likhet med laserstråleoppgaven kan elevene også her få utdelt hvert sitt svaralternativ, og deretter bli utfordret til å argumentere for hvilke premisser i oppgaveteksten som må endres slik at deres brikker blir det riktige svaret.

Å be elevene formulere de nye premissene kan fremme et behov for å finjustere argumentene slik at premissene blir presise. En annen mulighet er å gjøre endringer på brikkene. Elevene kan enten undersøke hvilken brikke som trenger færrest endringer for at deres svaralternativ blir riktige, eller ta utgangspunkt i sin utdelte brikke og argumentere for hvilke endringsbehov som må til. Vil det være nok å flytte på én del av veien på brikken, eller må det større endringer til?

Artikkelen ble først publisert i Tangenten 03/22.

Kilder

Boaler, J., & Humphreys, C. (2005). Connecting mathematical ideas: Middle school video cases to support teaching and learning (No. 1). Heinemann.

Davis, P., & Herch, R. (1981). The Mathematical Experience. In. Boston, USA: Birkhauser.

Jaworski, B. (2010). Collaborative inquiry in developing mathematics teaching in Norway The First Sourcebook on Nordic Research in Mathematics Education (pp. 71-90): Information Age Publishing.

Kunnskapsdepartementet. (2019). Læreplan i matematikk 1.–10. trinn (MAT01-05). Retrieved from https://data.udir.no/kl06/v201906/laereplaner-lk20/MAT01-05.pdf

Russel, S. Jo. (1999). “Mathematical reasoning in the Elementary Grades.” In Developing Mathematical Reasoning in Grades K-12.1999 NTCM Yearbook, L. Stiff (red.). Reston, VA: National Council of Teachers of Mathematics.

Volmink, J. (1990). The nature and role of proof in mathematics education. Pythagoras, 23, 7-10.

Yackel, E., & Hanna, G. (2003). Reasoning and proof. A research companion to principles and standards for school mathematics, 227-236.