10. trinn: Eksempeloppgave med graftegner

Del 2, oppgave 8

Oppgaven er hentet fra forslag til ny eksamensordning for MAT0010 Matematikk 10. årstrinn (2012, s.20). Oppgaven inneholdt også et bilde av en bil.

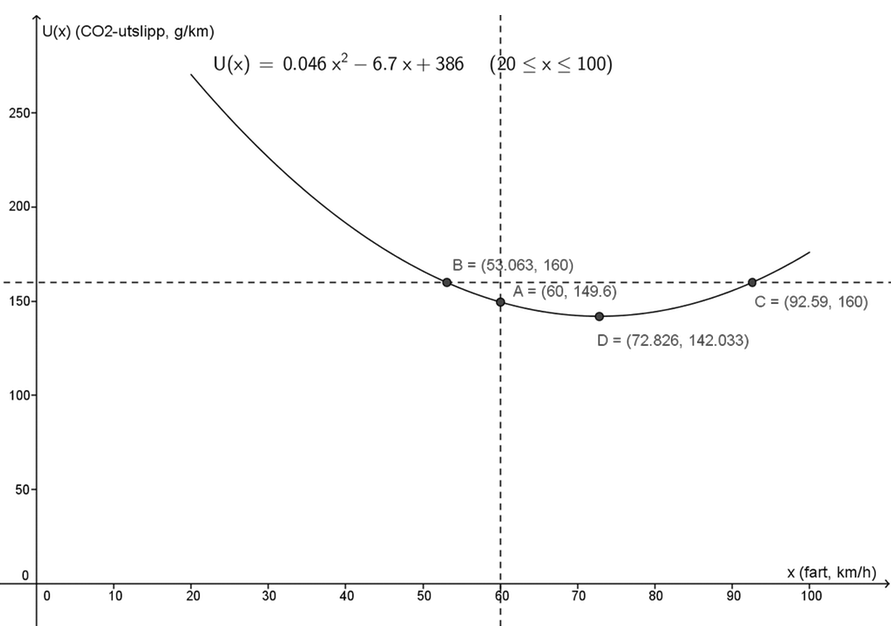
Utslippet U (målt i gram) av CO2 per kilometer for en bestemt bil er gitt ved \[U(x) = 0,046x^2 -6,7x + 386\] der x er farten målt i km/h.

      1. Tegn grafen til U i et koordinatsystem for 20 ≤ x ≤ 100. Bestem hvor mange gram CO2 bilen slipper ut per kilometer dersom den holder en fart på 60 km/h.

 

    • Bestem hastighetene som gir CO2-utslipp per kilometer på 160 g.
  • Bestem den farten til bilen som gir minst CO2-utslipp.

Løsningsforslag

graftegner2.PNG

 

      1. Jeg skriver x=60 og finner skjæringspunktet A der linja skjærer grafen.

        Bilen slipper ut 150 gram CO2 per km når den holder en fart på 60 km/h.

 

    • Jeg skriver y=160 og finner skjæringspunktene B og C der linja skjærer grafen.

      Hastighetene 53 km/h og 93 km/h gir utslipp på 160 g CO2 per km.

 

    • Jeg finner bunnpunktet D ved å bruke kommandoen Ekstremalpunkt[U].

      Bilen slipper ut minst CO2 når farten er 73 km/h.

 

Kommentarer til løsningsforslaget

Figuren viser at eleven har klart å tegne funksjonen i definisjonsområdet, og det er derfor ikke nødvendig med en forklaring. All viktig informasjon er flyttet fra algebrafeltet til grafikkfeltet, og derfor er det ikke nødvendig å ha med algebrafeltet i besvarelsen.

Oppgavene a, b og c er tekstoppgaver og krever derfor tekstsvar.

 

GeoGebra

Didaktiske refleksjoner
 

GeoGebra viser to desimaler som standard. Endre ved å gå inn på Innstillinger - Avrunding - 3 desimaler

I denne oppgaven er funksjonsuttrykket oppgitt med tre desimaler. Det er viktig å gjøre elevene oppmerksom ar de må tilpasse antall desimaler, ellers vil GeoGebra runde av funksjonsuttrykket som elevene taster inn.

a)

Skriver inn funksjonen U(x)=Funksjon[0.046x^2-6.7x+386,20,100].

Grafen blir ikke synlig før elevene tilpasser aksene. Det er en fordel å tilpasse x-aksen og y-aksen hver for seg. Zooming kan gi uoversiktlige grafikkfelt.

 

x = 60 og skjæringspunkt med grafen.

Alternativt kan man skrive U(60), og få funksjonsverdien direkte.

x=, y= og markering av skjæringspunkt er ofte viktig i oppgaver med funksjoner.

b)

y = 160

Har elevene god forståelse for uttrykkene x= og y=, og klarer å tolke dem, klarer de å løse de fleste oppgaver med funksjoner.

c)

Ekstremalpunkt[U]

Elevene må kjenne til begrepet ekstremalpunkt, og lære å bruke rullegardinen som kommer fram når de starter å skrive i inntastingsfeltet. GeoGebra bruker ekstremalpunkt som samlebegrep for toppunkt og bunnpunkt, og elevene må selv avgjøre om de aktuelle ekstremalpunktene er topp- eller bunnpunkt.