10. trinn: Eksempeloppgave med dynamisk geometriprogram

Denne oppgaven er hentet fra forslag til ny eksamensordning for MAT0010 Matematikk 10. årstrinn (2012, s. 40).

Det er ikke et krav at elever skal beherske dynamisk geometriprogram på eksamen, men elever som gjør det, vil ha en stor fordel dersom de skal løse geometrioppgaver på del 2 av matematikkeksamen. Bruk av dynamisk geometriprogram vil også være svært nyttig ellers i geometriundervisningen, og vi anbefaler at elevene blir kjent med slik programvare.

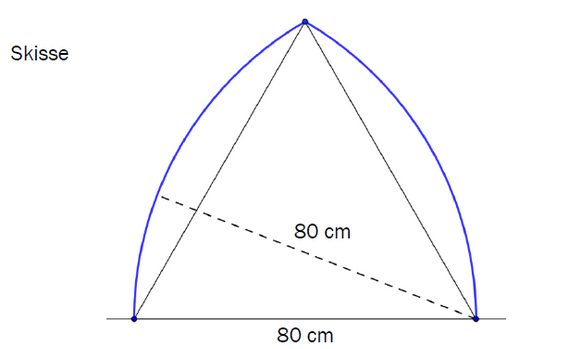
Nedenfor ser du en likesidet trekant med såkalte «gotiske buer».

a) Tegn figuren i målestokk 1:10.

b) Bestem arealet av figuren du har tegnet.

Løsningsforslag

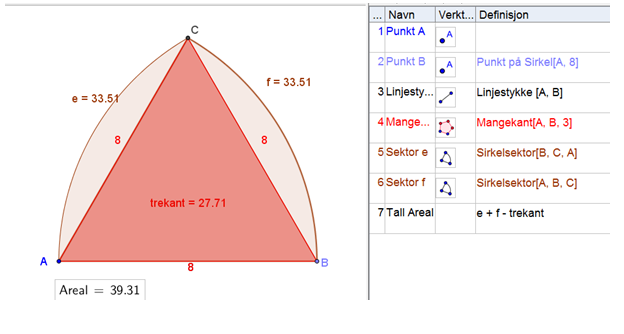
a) Se figuren.

b) Her følger tre mulige svaralternativer:

1. Jeg adderer arealet til sirkelsektorene e og f og trekker fra arealet av trekanten (se rad 7).

Det vil si at arealet er 39,31 cm².

2. Jeg legger sammen arealene av sirkelsektorene e og f og trekker fra arealet der sektorene ligger oppå hverandre, altså trekanten. Da sitter jeg igjen med arealet til den gotiske buen.

Arealet er 39.31 cm².

3. Arealet til trekanten er 27,71 cm². Arealet til hver av sirkelsektorene er 33,51 cm². Figuren består av en sirkelsektor og en rest. Jeg finner resten ved å trekke arealet av trekanten fra arealet av den ene sirkelsektoren: 33.51 cm²- 27,71 cm²=5,8cm².

Arealet til figuren blir dermed: 33,51 cm² + 5,8cm² = 39.31 cm².

Kommentarer

Alle tre svaralternativer er gode besvarelser. Bildet inneholder både selve figuren og konstruksjonsforklaringen, og verktøylinjeikoner gjør det enkelt å finne ut hvordan elevene har tenkt da de tegnet figuren.

Oppgaveteksten ber om at trekanten skal tegnes i målestokk 1:10, altså at figuren har en side på 8 cm. Tallet 8 i figuren viser at eleven har tegnet i målestokk 1:10. Det betyr imidlertid ikke at en utskrift av trekanten vil ha sidelengder på 8 cm. Vi mener det er urimelig å kreve at målene stemmer på en utskrift av eksamensbesvarelsen siden elevene ikke har kontroll på eventuell skalering i forbindelse med utskrift.

GeoGebra	Didaktiske refleksjoner
Tegn et linjestykke med lengde 8	Når det er lov å tegne figuren, betyr det at vi kan bruke alle verktøyene i GeoGebra. I motsetning hvis oppgaven ber om «å konstruere».
Tegn en regulærmangekant over linjestykket	Verktøyet som lager regulære mangekanter er mest effektivt. Alternativt kan elevene konstruere trekanten med sirkler. Da må de huske å finne alle skjæringspunktene, samt markere figuren som trekant slik at de kan finne arealet.
Bruk verktøyet sirkelsektor til å tegne figuren ferdig	Noen elever vil her tegne en «sirkelbue gjennom tre punkt». Figuren ser riktig ut, men man kan ikke beregne areal av en lengde. De må bruke «sirkelsektor».
Finn arealet med hjelp av algebra	Elever som får til denne oppgaven viser god forståelse. Først må de finne arealet til de enkelte figurene. Da er det viktig å bruke knappen «regulær mangekant» siden GeoGebra ikke oppfatter tre linjestykker som henger sammen som en trekant. Så må elevene finne ut hvilke figurer arealet består av (to sirkelsektorer minus arealet av trekanten).