Matematikk R1: Eksempeloppgave med dynamisk geometriprogram

Del 2, oppgave 11

Denne oppgaven er hentet fra forslag til ny eksamensordning for REA3022 Matematikk R1 (2012, s. 61). Det er ikke et krav at elever skal beherske dynamisk geometriprogram på eksamen, og en eksamensoppgave vil derfor være formulert noe annerledes enn dette eksempelet.

Elever som behersker et dynamisk geometriprogram vil ha en stor fordel dersom de skal løse geometrioppgaver på del 2 av matematikkeksamen. Bruk av dynamisk geometriprogram vil også være svært nyttig ellers i geometriundervisningen, og vi anbefaler at elevene blir kjent med slik programvare.

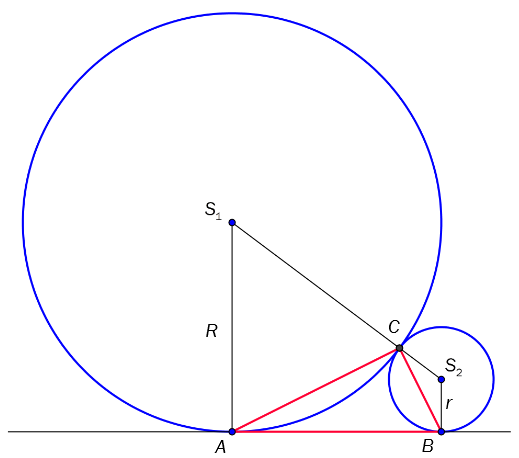
Sirkelen med radius R og sentrum S₁ tangerer en annen sirkel med radius r og sentrum S₂. Sirklene har en felles tangent med A og B som tangeringspunkter.

a) Vis at AB = 2`sqrt(Rr)`

b) Bruk dynamisk geometriprogram til å

tegne figuren for R = 4 og r = 1
kontrollere at `/_` ACB = 90°
kontrollere at `/_` BAS₁ = `/_` S₂BA = 90°

c) Forklar hvorfor en halvsirkel med diameter AB går gjennom punktet C.

Løsningsforslag

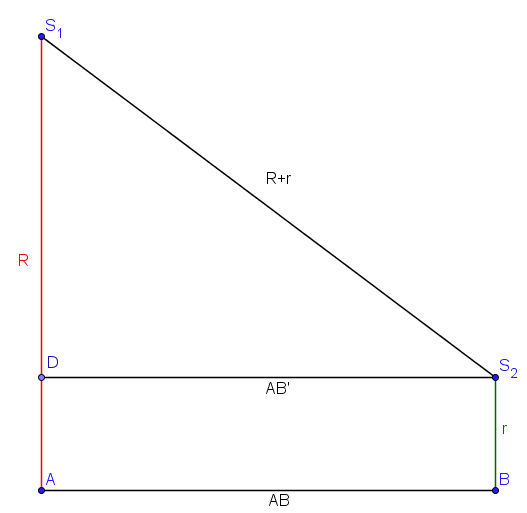
a) Jeg lager en skisse og ser at DS₂ må være like lang som AB (kaller derfor linjestykket AB').

Ved å bruke det jeg vet om den rettvinklede trekanten DS₁S₂ kan jeg finne lengden av AB' og dermed AB. Jeg bruker Pytagoras setning (rad 2) og får to løsninger. Den negative løsningen er ingen gyldig løsning (lengden må være positiv).

Dermed er det vist at AB = 2`sqrt(Rr)`.

Vinkel ACB, BAS₁ og S₂BA er alle 90 grader.

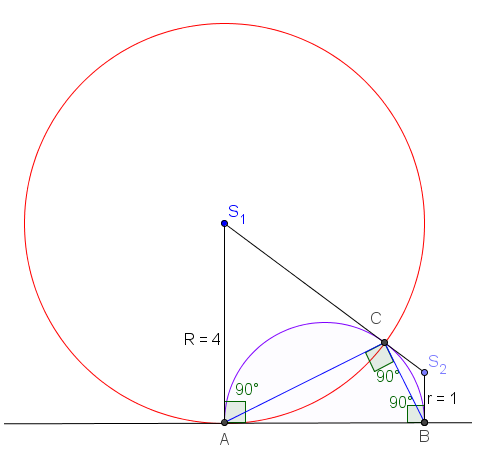
Jeg tegner opp en halvsirkel med lengde AB. Thales’ setning sier at et punkt C på halvsirkelen fra A til B, vil lage en rettvinklet trekant ABC uansett hvor C ligger på halvsirkelen.

Siden jeg allerede har vist at vinkel ACB er 90 grader, må C alltid ligge på halvsirkelen.

Kommentarer

Ved å bruke GeoGebra kan elevene lage en nøyaktig figur mye raskere enn for hånd. I tillegg kan de bruke programmets funksjoner til å beregne størrelser på vinkler, lage tangenter og så videre.

	GeoGebra	Didaktiske refleksjoner
a)	Det er alltid lurt å lage en skisse før elevene begynner arbeidet i CAS. Oppgaven er løst med CAS, men kan gjerne løses på papir.	Eleven i R1 skal være vant med å bruke CAS. Det kan være vanskelig for elevene å se den rettvinklede trekanten de kan bruke for å løse oppgaven. GeoGebra ikke godtar x som navn på et linjestykke.
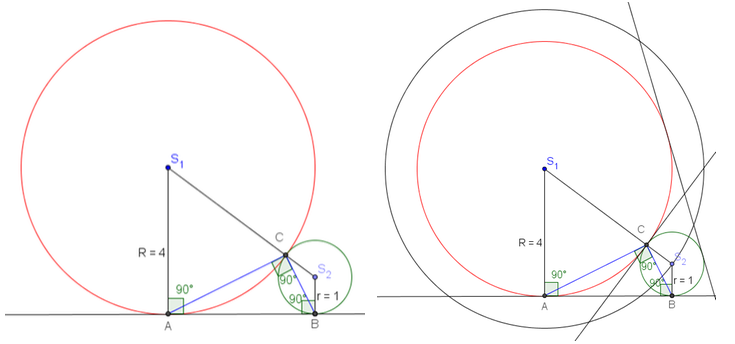
b)	Figuren er tegnet med bruk av alle tillatte hjelpemidler. Det er vanskelig å skyve sirklene slik at punkt C vises. Figuren inneholder mange detaljer så derfor er det valgt å ta et utsnitt av figuren for å vise vinklene.	Det er ikke nøyaktig nok å finne punkt C ved bare å skyve sirklene inn til hverandre: C er skjæringspunktet mellom to geometriske steder (sirkel med radius R+r og parallellen til tangenten med avstand r). Det er en omfattende konstruksjon. Derfor er konstruksjonsforklaringen forkortet ved å bruke etappepunkt. På eksamen er liggende format ofte best.
c)	Det er lurt med en ekstra tegning med halvsirkel som viser at påstanden faktisk stemmer	Begrepet Thales’ sirkel er ikke kjent for alle elever. Begrepene "sentralvinkel" og "periferivinkel" kan brukes i forklaringen istedet.