10. trinn: Eksempeloppgave med graftegner og CAS
Del 2, oppgave 9
Oppgaven er hentet fra MAT0010 Matematikk: Eksempel på eksamen våren 2015 (Utdanningsdirektoratet, 2014, s. 10). Det er krav om at elevene skal bruke graftegner på oppgave b).
Marius har x klinkekuler, Kathrine har y klinkekuler.
Marius: Gi meg 10 klinkekuler, så har vi like mange!
Kathrine: Hvis du i stedet gir meg 10 klinkekuler, så vil jeg ha dobbelt så mange som deg!
a) Vis at vi ut fra utsagnene til Marius og Kathrine kan stille opp følgende likningssystem
`[[x-y=-20],[2x-y=30]]`
b) Bruk graftegner til å bestemme hvor mange klinkekuler Marius har, og hvor mange klinkekuler Kathrine har.
c) Bestem ved regning hvor mange klinkekuler Marius har, og hvor mange klinkekuler Kathrine har.
Løsningsforslag
a) Jeg bruker utsagnene til Marius og Kathrine for å lage likningene:
Utsagnet til Marius kan settes opp som denne likningen: x+10 = y-10 som kan gjøres om til x-y = -20.
Utsagnet til Kathrine kan settes opp som denne likningen: 2(x -10) = y+10 som kan gjøres om til 2x-y = 30.
Det gir likningssystemet:
`[[x-y=-20],[2x-y=30]]`
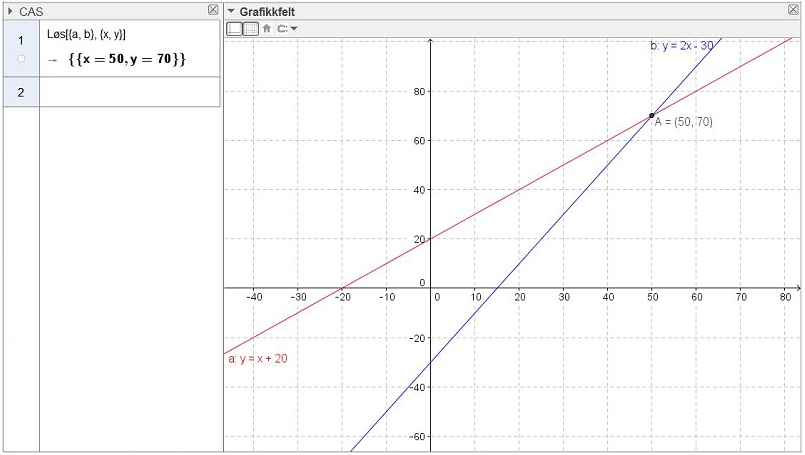
b) Jeg skriver inn likningene i inntastingsfeltet og finner skjæringspunktet mellom grafene for å finne antall klinkekuler (punkt A). Marius har 50 klinkekuler og Kathrine har 70 klinkekuler.
c) Jeg bruker CAS og finner at Marius har 50 klinkekuler og Kathrine har 70 klinkekuler.
Kommentarer
Det er ikke krav om at elever på 10. trinn skal beherske CAS på eksamen, men det kan være en fordel på eksamen.
|
|
GeoGebra |
Didaktiske refleksjoner |
|
a) |
|
Løses best på papir. Oppgaven er vanskelig da elevene må omforme likningene for å få dem i den oppgitte formen. |
|
b) |
Skriv inn likningene i skrivefeltet. |
Uansett hvordan elevene skriver inn likningene blir grafene tegnet. Avhengig av innstillingene, kan det hende de må zoome ut for å få se grafene. Det er lurt å vise navn på grafene i grafikkfeltet. Da er det ikke nødvendig å ha med algebrafeltet i besvarelsen. |
|
c) |
Skriv inn likningene i CAS og bruk "Løs". |
Når det står «Ved regning» i del 2, er det lov å bruke CAS. Elevene trenger bare å lime inn CAS i oppgavebesvarelsen og skrive et tekstsvar. I dette eksempelet bruker vi navnene på likningene (a og b) i stedet for de fullstendige uttrykkene i CAS, men elevene kan også skrive: Løs[{x-y=-20,2x-y=30}, {x,y}] . |