GeoGebra-ressurser fra Matematikksenteret og Kikora

Blogg

20.04.2022

Illustrasjon med logoen til Matematikksenteret, Kikora og GeoGebra

Matematikksenteret og Kikora har samarbeidet om å utvikle undervisningsopplegg i GeoGebra. I denne bloggen vil vi vise eksempler på oppgaver, samt hvordan arbeidet med oppgavene kan foregå i tråd med læreplanen (LK20).

GeoGebra støtter elevene i å utvikle sitt matematisk språk og gjør det naturlig å veksle mellom ulike representasjoner. Elever som lærer å kombinere ulike deler av programmet, vil ha et godt utgangspunkt for å utforske. Vi vil her gi noen eksempler på oppgaver hvor elevene lærer å bruke GeoGebra samtidig som de kan utvide sin matematiske forståelse. Oppgavene gir elevene varierte erfaringer mens de utforsker, resonnerer og argumenterer.

Lær GeoGebra

I Lær GeoGebra blir elevene kjent med verktøyene i GeoGebra. Målet er at de skal bli i stand til å bruke GeoGebra når de har behov for det. De første undervisningsoppleggene passer til alle elever, mens de siste er best egnet for elever på studiespesialiserende studieretninger. Lærerveiledningene sier noe om hva elevene må kunne på forhånd og hva de lærer om i opplegget. Vi anbefaler at alle elevene starter med Geometri der de tegner figurer, endrer farger, viser navn og lignende. Vi oppfordrer til arbeid i par slik at elevene kan diskutere underveis.

Selv om Lær GeoGebra har fokus på opplæring i GeoGebra, legger mange av oppgavene opp til utforsking og samtale om matematiske egenskaper, noe som blir vektlagt i LK20. Elevene lærer å bruke verktøy i GeoGebra og å bevege på figurene for å observere hva som skjer. I Geometri skal for eksempel elevene tegne parallelle linjer og deretter bevege ulike deler av figuren (Figur 2). Elevene vil oppdage at linjene de har tegnet alltid er parallelle med den opprinnelige linjen, uansett hvordan de drar i figuren.

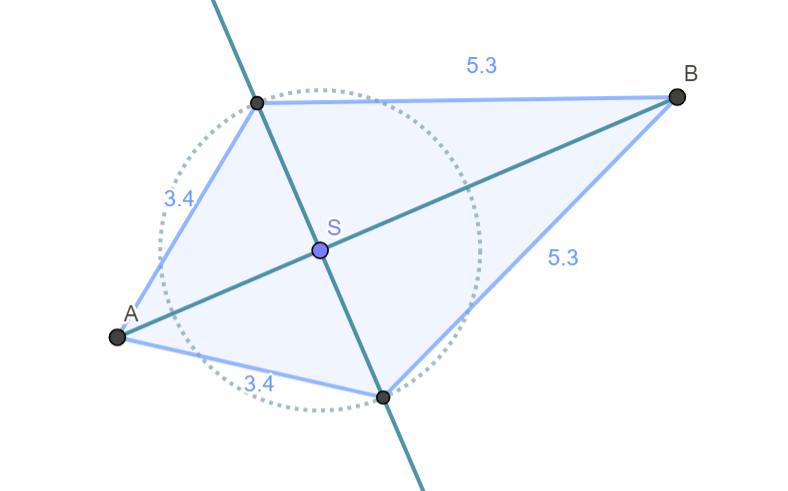
Et annet eksempel er i Mangekanter der elevene skal tegne og utforske en drage (Figur 3). Etter å ha lært om verktøyene de trenger for å tegne en drage i GeoGebra, skal de dra i dragen slik at den først blir en rombe og så et kvadrat. Elevene må bruke kunnskapene de har om geometriske figurerer for å resonnere seg fram til hva de må gjøre. De vil oppdage at dragen blir til et kvadrat når alle hjørnene ligger på sirkellinjen. Slik kan elevene erfare at alle kvadrater har en omskreven sirkel og et kvadrat er et spesialtilfelle av en drage og en rombe.

GeoGebra - illustrasjon som ligner drage — Figur 3

I mange av eksemplene skal elevene selv bevege på figurer, men i GeoGebra kan de også animere objekter. Små animasjoner er plassert i oppleggene for å hjelpe elevene med å forstå hva som skjer og hvorfor. Elevene kan lære mer om å animere objekter i Animasjoner.

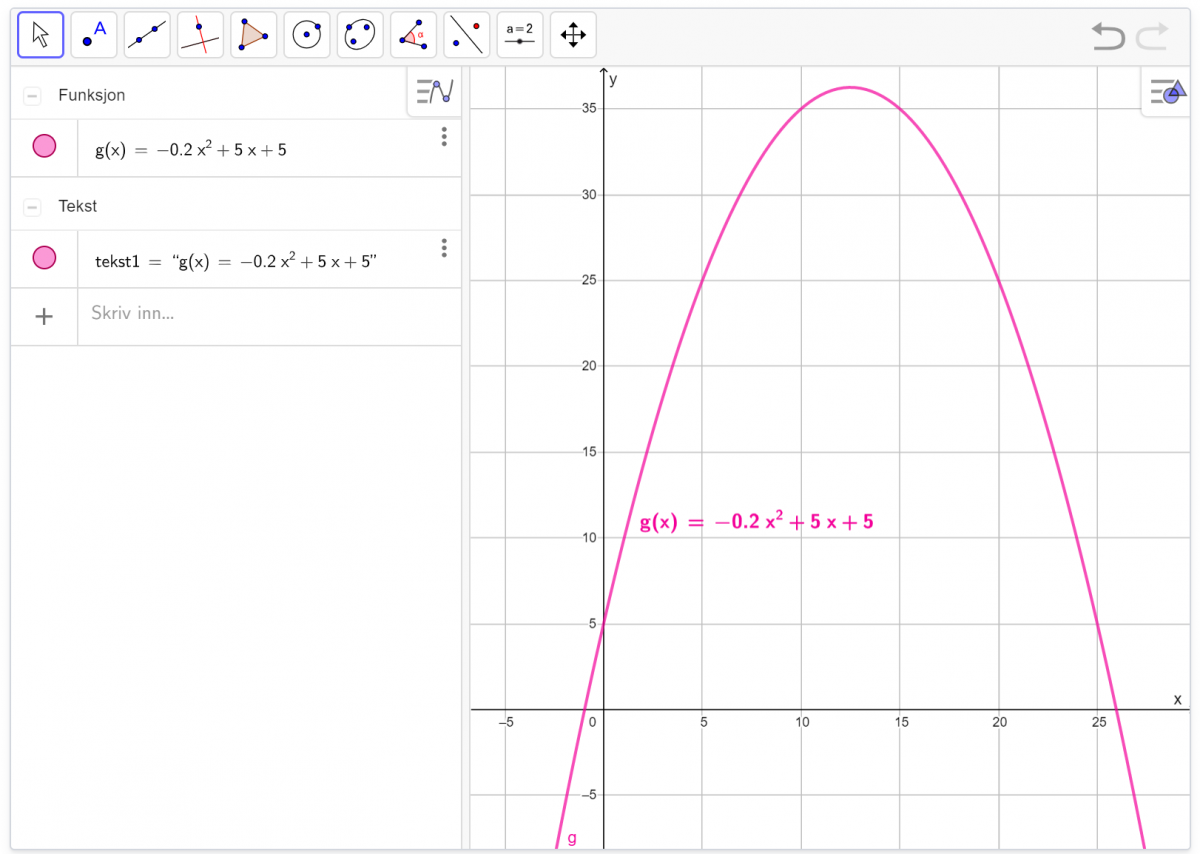
Elevene skal kunne presentere arbeidet sitt i GeoGebra på en oversiktlig og ryddig måte. Det visuelle uttrykket har stor betydning og derfor skal elevene i mange av oppgavene endre farge, justere akser, gi nytt navn og lignende. I Funksjoner 1 skal for eksempel elevene dra funksjonsuttrykket fra Algebrafeltet til Grafikkfeltet og gi det samme farge som grafen (Figur 4). Da blir funksjonsuttrykket til en tekst som elevene kan plassere akkurat der de ønsker.

Bruk GeoGebra

I Bruk GeoGebra er målet er at elevene skal utvikle en dypere forståelse av et matematisk tema. Lærerveiledningene til disse undervisningsoppleggene er grundige og viser hvordan oppgavene kan brukes i kombinasjon med klassediskusjon og andre aktiviteter. Det er likevel ikke noe i veien for at elevene kan gjøre oppgavene på egen hånd, selv om utbyttet ikke nødvendigvis blir det samme.

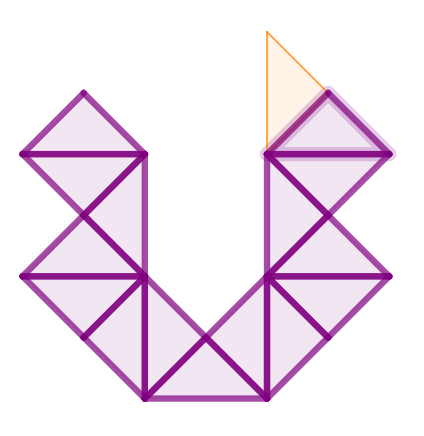
Undervisningsopplegget Speiling om linjer og sidekanter egner seg godt for barnetrinnet. Verktøylinjen i GeoGebra er tilpasset slik at elevene bare ser verktøyene som er nødvendige. I oppgavene kan de utforske speiling av punkter og figurer på en annen måte enn med papir og blyant. For eksempel skal elevene speile en figur slik at den dekker en annen figur. Det finnes mange måter elevene kan løse oppgaven på. Kikora vil godkjenne alle løsninger uansett hvor mange speilinger de gjør. Elevene kan gjøre oppgavene flere ganger og kanskje erfare at noen løsninger er mer effektive enn andre (Figur 5).

Illustrasjon av speiling av trekant i Geogebra — Figur 5

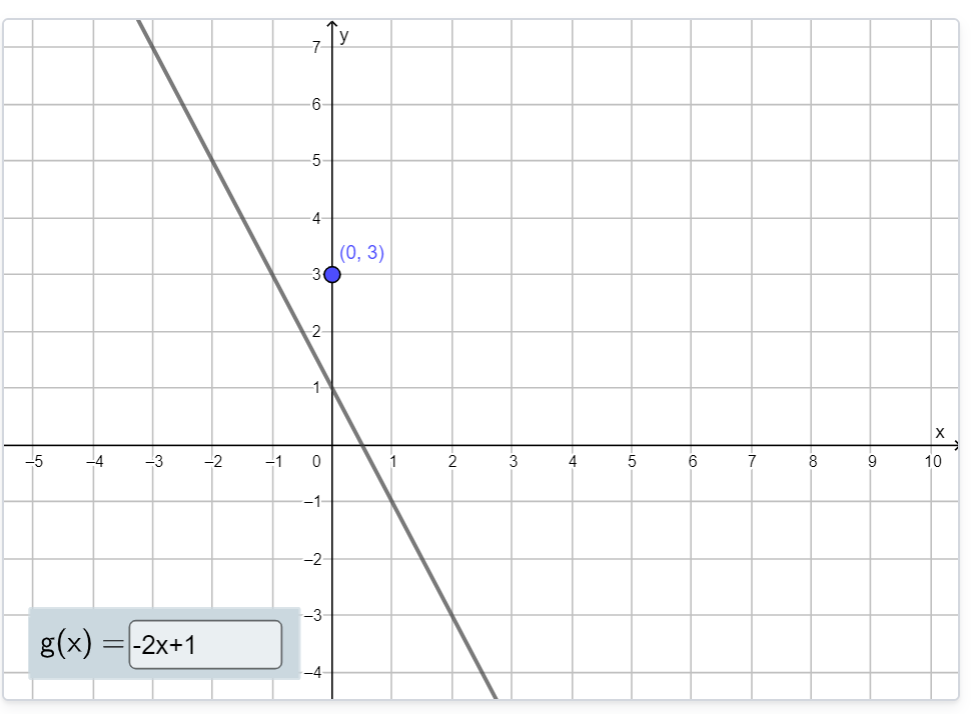
I Finn Funksjonsuttrykket 1 og 2 blir elevene kjent med stigningstall og konstantledd til lineære funksjoner på en annen måte enn med papir og blyant. For eksempel skal elevene finne en lineær funksjon som går nedover og gjennom et gitt punkt. Når elevene skriver inn et forslag til funksjonsuttrykk, tegner Kikora grafen. Da kan elevene se om grafen passer og eventuelt endre funksjonsuttrykket (Figur 6). Det finnes mange løsninger og Kikora godtar alle.