Matematisk observasjon

Observasjon er den første naturvitenskaplige ferdigheten elevene utvikler. Når elevene observerer gjør de mer enn å se. De samler informasjon, gjenkjenner likheter og ulikheter, gjenkjenner sekvenser og hendelser, oppdager mønster, og ikke minst forstår observasjonene sine. Elevene kan bruke alle sansene når de observerer (Rahman, 2019). Observasjon er viktig for å utvikle og utvide forståelse i matematikk. Det er imidlertid ikke like opplagt hva det betyr å observere i matematikk som i noen av de andre realfagene. Når elevene skal utforske, løse problemer og lage modeller må de observere underveis i prosessen. En konsekvens av dette er at elever som strever med å observere, også vil ha utfordringer med å resonnere, argumentere og generalisere. Observasjon er derfor viktig for at elevene skal mestre kjerneelementene i matematikk.

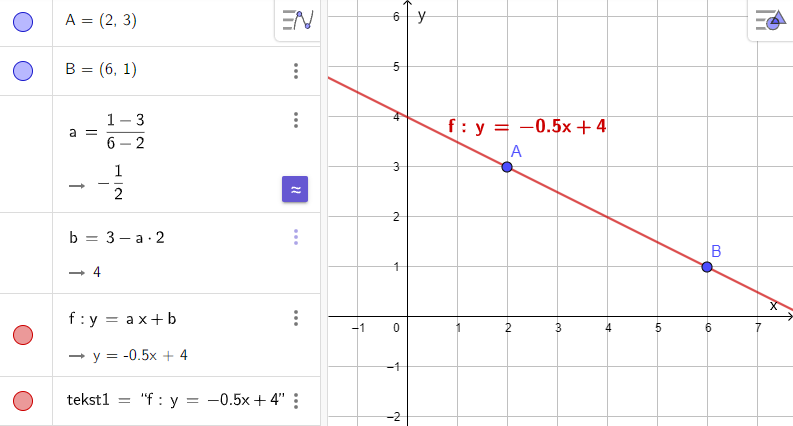
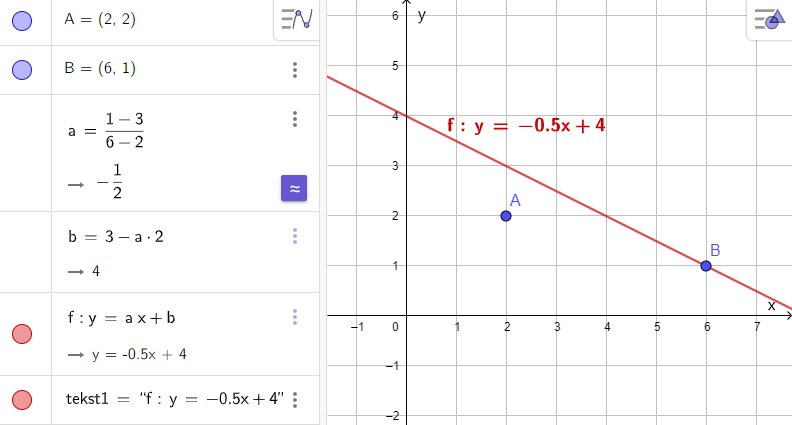
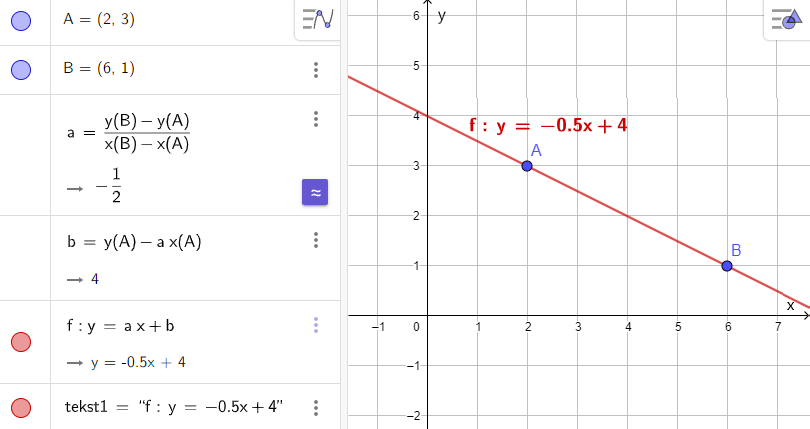
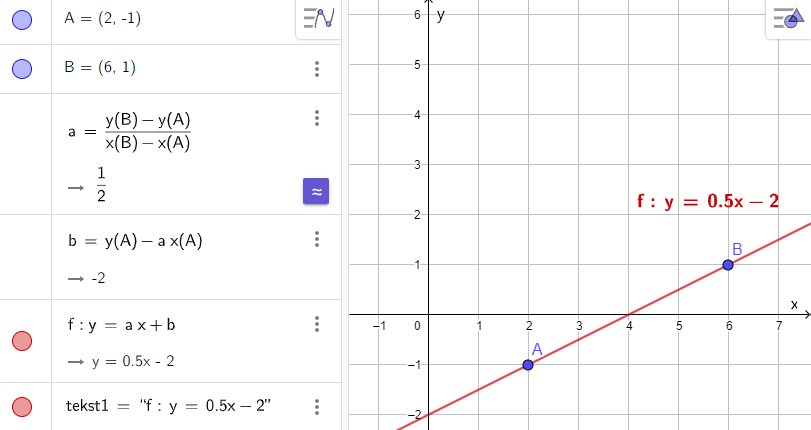
I et opplegg for å trene elevene på observasjon ble elevene bedt om å lage et uttrykk for en linje gjennom to gitte punkter i GeoGebra. Først skulle de bruke tallkoordinatene til punktene (figur 1-2), og etterpå variabler (figur 3-4). I eksemplet med tallkoordinater følger ikke linjen med når de drar i punktene. Derimot vil linjen alltid gå gjennom punktene hvis elevene bruker variabler.

Mange av elevene observerte at uttrykket for linjen endret seg når de beveget punktene i eksemplet med variabler. Observasjonen er riktig, men den fører ikke til en utvidet forståelse for variabler. Elevene som var dyktige til å observere sammenlignet de to uttrykkene og gjenkjente likheter og ulikheter mellom dem, og forstod at forskjellen er bruk av variabler. De kunne dermed utvide forståelsen ved å observere sammenhengen mellom variablene, punktene og linjen.

Det er lett å ta elevenes observasjonsferdighet for gitt, men i likhet med andre ferdigheter krever det øving for å bli god til å observere. Elevene kan utvikle gode observasjonsferdigheter hvis de får varierte erfaringer med å observere og hvis de de får diskutere observasjoner med andre.

GeoGebra kan gi elevene en arena hvor de kan øve på å observere. Programmet har mange verktøy og lager nøyaktige figurer. Det er også lett å endre og lett å angre. Det kan være lurt å endre innstillingene slik at GeoGebra ikke lager navn på nye objekter (i Grafikkfeltet) slik at elevene ikke blir forstyrret av det i observasjonsprosessen.

Nå skal vi presentere noen aktiviteter hvor elevene kan øve på å observere.

Aktivitet 1: Linje og punkter

En aktivitet som det kan være fint å starte med er å la elevene tegne en linje i GeoGebra. Linjen får automatisk to punkter. Elevene bør endre fargen til punktene (rosa og grønn på figur 5) slik at det blir lettere å beskrive hva de observerer. Lag så et nytt punkt på linjen (blå på figur 5). Så skal elevene observere mens de drar i punktene og linjen.



 

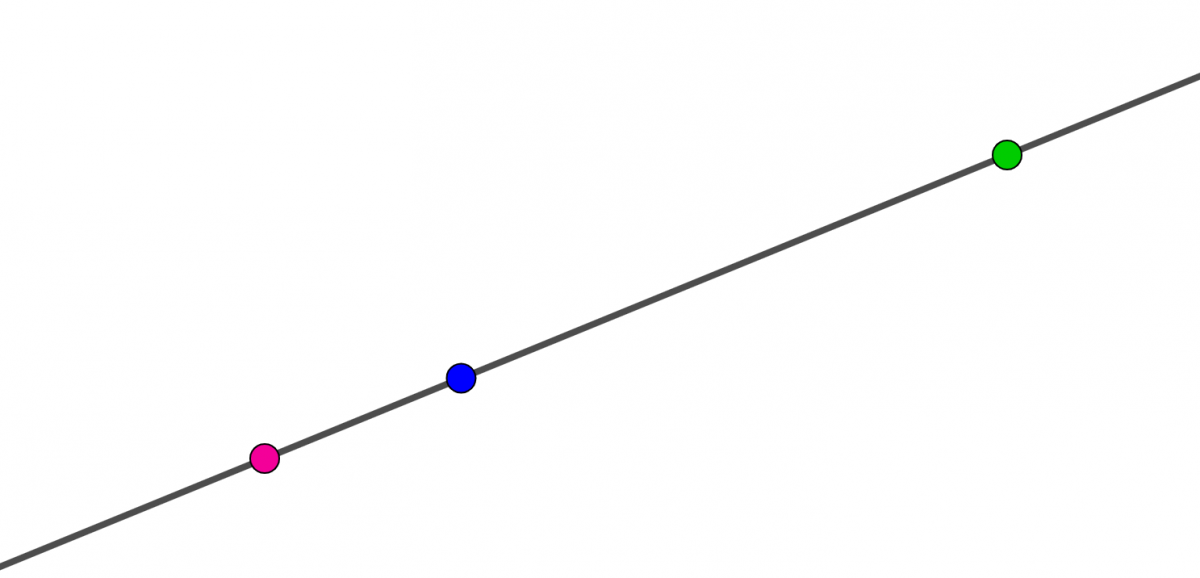
Når elevene har fått god tid til å undersøke figuren, skal de forklare hva de har oppdaget til medelever. Det er like viktig å høre på andre elever sine forklaringer som å forklare egne observasjoner. La elevene sammenligne ulike forklaringer. Det er ikke opplagt at flere forklaringer kan handle om det samme.

Mulige elevobservasjoner:

• Hvis jeg drar i det grønne punktet, følger det blå punktet med.
• Hvis jeg drar i det rosa punktet, følger linjen med.
• Hvis jeg drar i det rosa punktet, følger det blå punktet med.
• Hvis jeg drar i linjen, følger alle punkter med.
• Punktene ligger alltid på linjen.
• Linjen beveger seg ikke hvis jeg drar i det blå punktet.

Den siste observasjonen skiller seg fra de andre. Mange elever vil slutte å observere når de har funnet ut at de hva de kan bevege. Men i matematikk er det også sentralt å finne ut hva som ikke beveger seg, altså hva som er konstant.

Aktivitet 2: Regulære mangekanter

På mellomtrinnet lærer elevene om egenskapene til todimensjonale figurer. De kjenner til begreper som vinkler og kanter og hjørner fra før. Det gir et godt utgangspunkt for å øve på å observere egenskapene til likesidede (regulære) mangekanter i GeoGebra. Elevene starter med å lage en heltall-glider n med intervallet 3-15. Så lager de en regulær mangekant og velger antall hjørner lik n (figur 6). Nå kan elevene observere hva som skjer når de endrer glideren eller grunnlinjen.

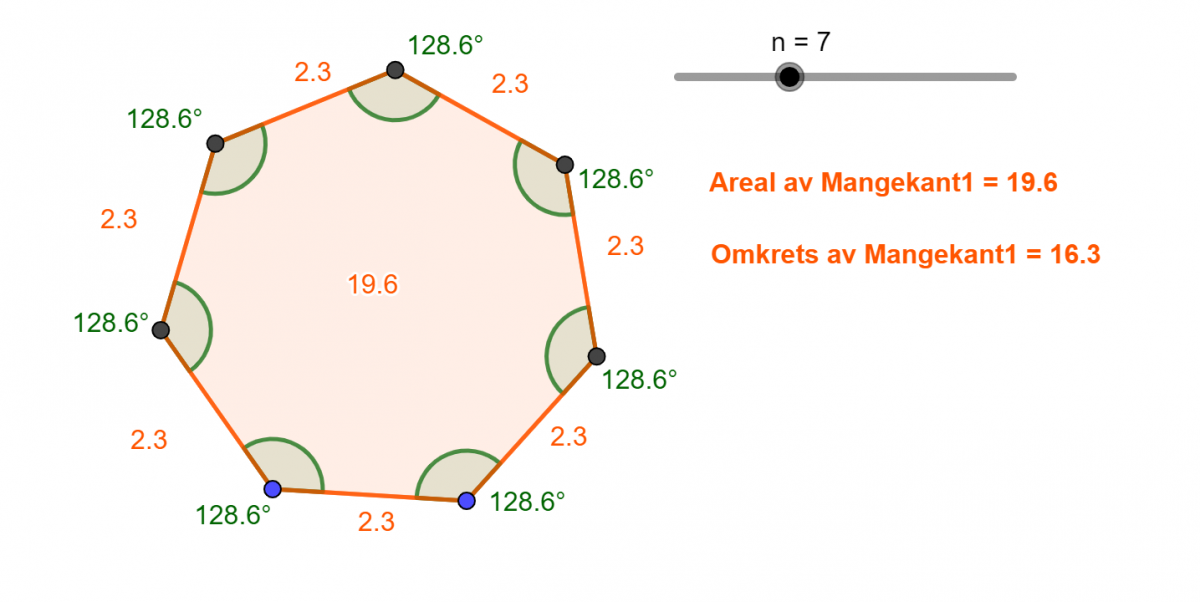
Gi elevene god tid til å sette ord på og forklare for hverandre. Oppfordre gjerne elevene til å ta i bruk flere verktøy som støtte i observasjonsprosessen. For eksempel kan GeoGebra vise størrelsen på vinkler, lengden på sider, omkrets og areal. 

Mulige elevobservasjoner:

• Hvis jeg drar i glideren, endrer antall sider seg.
• Sidene er fortsatt like lange når jeg drar i glideren.
• Alle vinklene inni figuren er like store.
• Alle sidene i figuren er like lange.
• Vinkelen blir større når figuren får flere sider.
• Hvis jeg drar i ett av punktene, endrer lengden på alle sidene seg.
• Omkretsen blir større når antall sider øker.

Elevene samler informasjon mens de beveger punkter og drar i glideren. De undersøker hva som endrer seg og hva som ikke endrer seg, og knytter det til begreper og erfaringer de har fra før. De oppdager mønster, for eksempel at omkretsen øker med antall sider. Denne observasjonen er et godt utgangspunkt når elevene skal finne egenskapene til likesidede mangekanter. Når elevene forstår observasjonene sine, kan de koble observasjonene til begreper de kjenner fra før. De vet at omkretsen er summen av lengden til alle sidene. Sammen med observasjonen av at alle sidene er like lange, kan elevene finne ut at omkretsen til likesidede mangekanter er sidelengde ganger antall sider.

Aktivitet 3: Lineære funksjoner med glidere

Lineære funksjoner og tilhørende funksjonsuttrykk er kjent for elevene på ungdomstrinn og i videregående skole. Det er en fordel når elevene skal øve på å observere. De har allerede en del begreper og erfaringer som de kan bruke i observasjonsprosessen. I tillegg må elevene vite hvordan de skriver inn funksjonsuttrykk i GeoGebra og kjenne til verktøy som kan hjelpe i observasjonsprosessen som Nytt punkt, Skjæring mellom to objekt, Stigning og Vis spor.

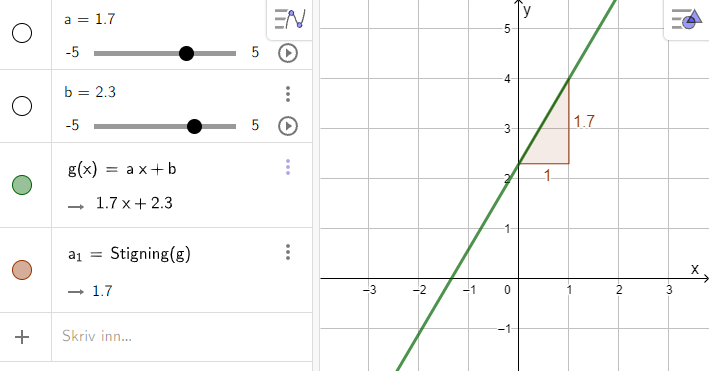
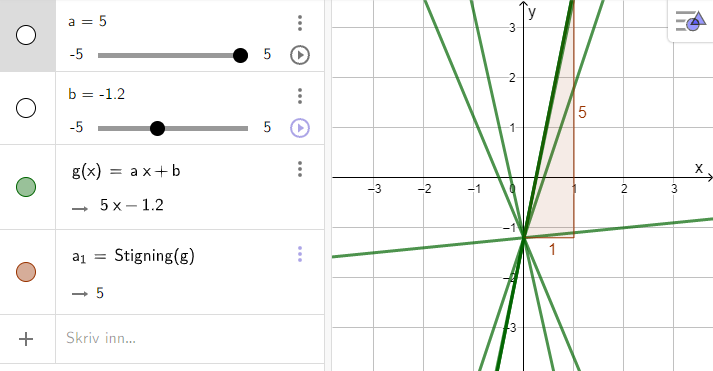
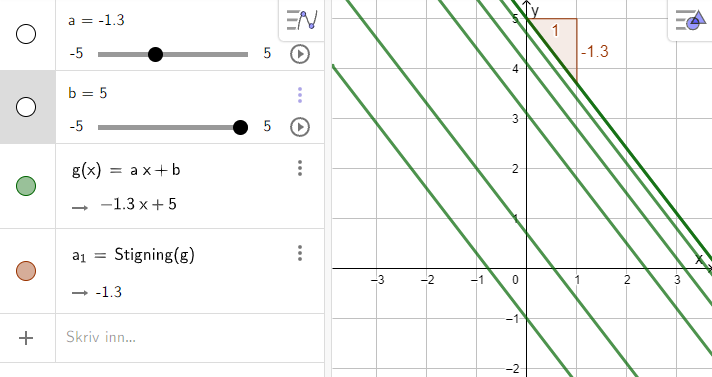
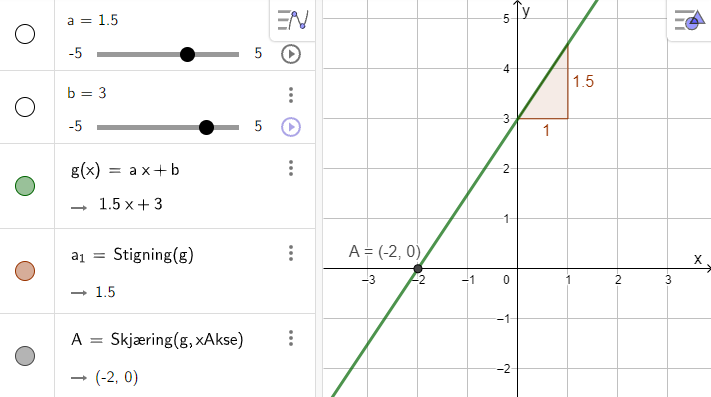
Be elevene skrive inn g(x)=a·x+b i GeoGebra. Programmet lager da glidere for a og b. Pass på at programmet viser minst 1 desimal. Så skal elevene observere. Hva oppdager de? Hva endrer seg? Hva endrer seg ikke? La elevene oppdage at det er lurt å endre en ting om gangen.

Mulige elevobservasjoner:

• Glider a styrer hvor bratt grafen er.
• Når a er 0 er grafen vannrett.
• Når jeg drar i glider b, flytter grafen seg opp og ned i koordinatsystemet.
• Hvis jeg endrer glider b, er grafen fortsatt like bratt.
• Når glider a er negativ, peker grafen nedover.
• Hvis jeg endrer glider a, skjærer fortsatt grafen y-aksen på samme sted.
• Grafen skjærer y-aksen i punktet (0, b).
• Glider a bestemmer stigningstallet til grafen.
• Glider b bestemmer konstantleddet til grafen.
• Grafen skjærer x-aksen der x = -b/a.

Elevene kjenner til dette uttrykket for lineære funksjoner fra før, men observasjonsprosessen kan gi økt forståelse for sammenhengen mellom graf og uttrykk. Elevene skal fokusere på å lage gode beskrivelser av egne observasjoner og sammenligne disse med medelever sine. Hvordan henger observasjonene sammen med det elevene kan fra før? 

Elever som trenger mer utfordringer kan observere funksjonsuttrykket f(x)=u∙(x-v)+w. Dette er et annet uttrykk for lineære funksjoner som er mer ukjent for elevene. Hva skjer hvis elevene drar i gliderne? Hva er likhetene mellom g(x) og f(x)? Hva er forskjellene? I observasjonsprosessen vil elevene ha stor nytte av å kunne skrive inn punkter med variabler i GeoGebra (se observasjon med fet skrift).

Oppsummering

Øvelse gjør mester! Elevene blir bedre til å observere med erfaring. Ved å sammenligne og diskutere observasjoner i helklasse, vil elevene utvikle sine egne observasjonsferdigheter. Det er viktig at læreren støtter elevene i prosessen, for eksempel ved å la elevene snakke om likheter og ulikheter til forklaringene. Et godt spørsmål for å bygge bro mellom observasjon og forståelse kan være «Hvorfor er det slik?».

Målet med å observere er å gi elevene et godt utgangspunkt for å knytte sammen nye erfaringer med kjente begreper og sammenhenger. Vi håper at aktivitetene har inspirert dere til å arbeide mer med observasjon i klasserommet slik at elevene får et best mulig utgangspunkt for å mestre kjerneelementene.

Referanser

Rahman, M. (2019). 21th century skill “problem solving”: Defining the concept. Asian Journal of interdisciplinary research, 2(1), 64-74.