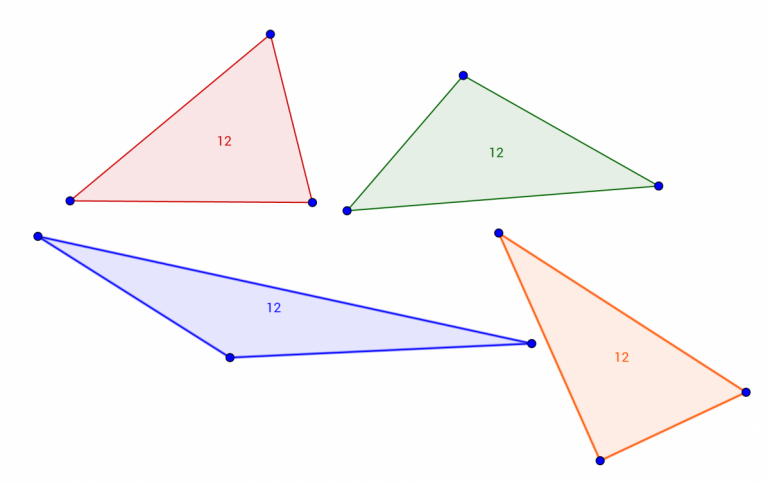
Trekant med areal 12

Arealet til trekant, algebra, høyde i trekant, GeoGebra

Hver elev trenger en PC med GeoGebra og elevarket. Det er en fordel for elevene om elevarket blir gjort tilgjengelig digitalt slik at de kan legge inn figurer og tekst

Elevene arbeider i GeoGebra på hver sin PC, men de sitter i par så de kan diskutere. Opplegget har som mål å gi en dypere forståelse av arealet til trekanter. Mange elever klarer å finne arealet ved hjelp av formler uten at de forstår sammenhengen mellom variablene. I dette opplegget trenger elevene kunnskapene fra algebra for å finne alle mulige trekanter med areal 12.

Forberedelse

Opplegget er godt egnet til å la elevene øve på føring av oppgaver digitalt, slik de skal gjøre på eksamen. Elevene kan lage sin egen Wordfil der de skriver inn svar og limer inn bilder fra GeoGebra. Alternativt kan læreren la elevarket være tilgjengelig digitalt slik at elevene kan skrive inn svarene og lime inn resultatene fra GeoGebra.

Det er en stor fordel om elevene blir kjent med utklippsverktøyet slik at de enkelt kan ta bilde av et valgt utsnitt i GeoGebra-vinduet, og deretter lime inn bildet i et tekstdokument. Vi anbefaler at elevene fester utklippsverktøyet på oppgavelinjen slik at det er lett tilgjengelig gjennom hele skoleåret. Utklippsverktøyet kan brukes i alle program, og eleven slipper dermed å forholde seg til mange ulike utskriftsmuligheter.

Figur 1: Utklippsverktøy  

Aktivitet 1

Oppgavetekst fra elevark

• Bruk verktøyet Mangekant og tegn fire trekanter.  Vis arealet til figurene.
• Flytt på hjørnene slik at alle figurene dine har areal som er så nær 12 som mulig.
• Lim trekantene inn i dokumentet. 
• Beskriv så nøyaktig som mulig hvordan du har tenkt og hva du har gjort.
• Hvilke fellestrekk finner du mellom trekantene? Er du fornøyd med resultatet?

Kommentarer til læreren

Elevene skal komme fram til svaret gjennom å prøve og feile, og med litt tålmodighet klarer de fleste elever å lage trekanter med areal 12. Målet med aktiviteten er å gjøre elevene bevisst på at det finnes mange ulike trekanter med areal 12 (se tittelbilde). Læreren må godta at noen elever er fornøyde med at arealet er omkring 12. Oppgaven blir enklere ved å velge en eller ingen desimal under Innstillinger. 

Aktivitet 2

Oppgavetekst fra elevark

• Åpne en ny GeoGebrafil.
• Velg Linjestykke med fast lengde. Skriv inn 8 i dialogboksen.
• Tegn en trekant der linjestykket med lengde 8 er en side.  Vis arealet.
• Flytt på hjørnene slik at arealet blir lik 12.
• Gjør det samme en gang til slik at du har to trekanter med side 8 og areal 12 på arket.
• Lim trekantene inn i dokumentet.
• Sammenlign med figurene som du laget i aktivitet 1. Var det lettere eller vanskeligere å få lage disse trekantene? Gi en begrunnelse.

Kommentarer til læreren

Når elevene tegner et linjestykke med bestemt lengde, vil linjestykket alltid legge seg parallelt med sidekanten til Grafikkfeltet (horisontalt). Dersom elevene kun får erfaring med figurer som har sider som ligger parallelt med sidekanten, kan det føre til dårlig forståelse av egenskapene til figurer. Det er derfor lurt å be elevene om å bevege litt på linjestykket (se figur 2).

Selv om den ene siden er kjent, er det ikke nødvendigvis lettere for elevene å finne trekanter med areal 12. Elevene kan ikke lenger dra i alle hjørnene til trekanten, men selv med en felles egenskap kan elevene finne mange ulike trekanter.

Figur 2: Trekanter som ikke er parallelle med sidekantene til Grafikkfeltet.

Aktivitet 3

Oppgavetekst fra elevark

Denne oppgaven besvarer du uten å bruke GeoGebra.  Bruk det du vet om trekanter.

• Hva må du vite for å kunne finne arealet til trekanter?
• Hvorfor finnes det uendelig mange trekanter med areal 12 og side 8?
• Hva er felles for alle trekanter med areal 12 og side 8?

Kommentarer til læreren

I denne aktiviteten skal elevene notere kunnskapene de har om beregning av areal, for eksempel kan de skrive ned formelen for arealet til trekanter og beskrive den med ord. Videre skal elevene begrunne hvorfor de kan tegne uendelig mange trekanter med areal 12 og side 8. Elevene har arbeidet med arealformelen for trekanter mange ganger. Likevel vil mange ha vanskeligheter med å se hvordan en formel og en tegning henger sammen. Det er ikke selvsagt for alle elever at side 8 kan være grunnlinjen når den ligger på skrått på arket, eller at alle sidene kan være grunnlinjen til trekanten, og dermed brukes til å beregne arealet til trekanten. I neste aktivitet skal elevene utforske at alle trekanter med areal 12 og en side på 8 har samme høyde.

Aktivitet 4

Oppgavetekst fra elevark

Åpne en ny GeoGebra-fil

• Tegn et linjestykke med lengde 8. Flytt litt på en av endepunktene slik at linjen ikke ligger parallelt med sidekanten til Grafikkfeltet.
• Tegn tre trekanter med areal 12 der linjestykket med lengde 8 er en av sidene.
• Hva observerer du? Tegn gjerne hjelpelinjer hvis det hjelper deg med å forklare.

Kommentarer til læreren

Når elevene har tegnet figuren med tre trekanter med samme grunnlinje, skal de se at det er mulig å tegne en linje gjennom alle punktene C. Denne linjen er parallell med grunnlinjen c.

I GeoGebra er det ikke lett å måle avstanden mellom paralleller, og derfor forventes det ikke at elevene skal gjøre det. Hvis læreren vil vise høyden, er det enklest å tegne en loddrett linje gjennom et punkt C, finne skjæringspunktet med grunnlinjen og tegne inn linjen mellom to punkt.

Figur 3 viser et eksempel på hvordan figuren vil se ut hvis elevene ikke tegner trekanter med nøyaktig areal 12. Da blir ikke høyden nøyaktig 3, og linjene er ikke parallelle. Elevene vil likevel oppfatte linjene som parallelle.

Figur 3: Tre trekanter med samme grunnlinje og areal 12.

Klassesamtale

Når de fleste elever har kommet godt i gang med aktivitet 4 og noen har startet med aktivitet 5, er det lurt med en felles oppsummering av arbeidet så langt. Elevene arbeider ikke like fort, og derfor er det viktig å ikke vente med en oppsummerende samtale til alle elevene er ferdige. Mye av hjelpen som elevene kan gi hverandre ville da gå tapt. I klassesamtalen kan læreren kontrollere om alle elevene har forstått at det finnes en sammenheng mellom tegningene og formel for areal og hvorfor det finnes uendelig mange trekanter med areal 12 og side 8.

 Ikke alle elever er klar over at avstanden mellom to parallelle linjer er lik uansett hvor de tegner den inn. Mange elever tenker at høyden må gå fra et bestemt punkt til motsatt side, så noen elever vil oppleve det som nytt at de kan tegne inn høyden hvor som helst på de to parallellene. Læreren må avgjøre hvor mye hjelp elevene trenger for å komme videre, for eksempel om elevene trenger hjelp til å tegne to parallelle linjer med en gitt avstand (se figur 4).

Det kan være lurt å gjøre aktivitet 5 i felles klasse siden fremgangsmåten for å tegne parallelle linjer i GeoGebra er noe forskjellig fra fremgangsmåten med papir og blyant. Ved å gjøre aktiviteten i fellesskap, får også alle elevene samme utgangspunkt for å prøve seg på aktivitet 6.

Figur 4: Fremgangsmåte for å tegne to parallelle linjer med en gitt avstand.

Aktivitet 5

Oppgavetekst fra elevark

Åpne en ny GeoGebra-fil.

• Nå skal du bruke kunnskapene fra aktivitet 3 og observasjonene fra aktivitet 4 til å tegne en trekant med grunnlinje 8 og areal 12 hvor arealet ikke endrer seg uansett hvordan du flytter på hjørnene. Se på GeoGebra-hjelp dersom du trenger noen ideer. Bildet viser starten av konstruksjonen.

• Forklar hvordan du tenker.

Kommentarer til læreren

Elevene starter med å tegne grunnlinjen. Minn de gjerne om å bevege grunnlinjen slik at den ikke ligger parallelt med sidekanten til Grafikkfeltet. Tegn en parallell i avstand 3 (høyden til trekanten) og sett et punkt hvor som helst på parallellen. Tegn trekanten.

Dette er en vanskelig oppgave som vi ikke kan forvente at alle elever klarer selvstendig, og derfor anbefaler elevene og læreren løser oppgaven i fellesskap.

Aktivitet 6

Oppgavetekst fra elevark

I denne oppgaven skal du lage en trekant med areal 12. Tallet 8 fra den siste oppgaven må du erstatte med en bokstav. Du kan velge hvilken som helst bokstav. I forklaringen er det valgt c.

• Tegn Linjestykke mellom to punkt og gi det navnet c.
• Når du skal tegne sirkelen, må du sette inn en formel for radius. Tenk over hvordan du regnet for å finne radius i aktivitet 5.
• For å gjøre ferdig trekanten, tegner du videre som i aktivitet 5.
• Test tegningen din ved å dra i hjørnene. Ta flere bilder og lim dem inn i dokumentet.
• Forklar hvorfor alle trekantene dine har areal 12.

Kommentarer til læreren

I denne aktiviteten har elevene bruk for algebrakunnskapene sine. De begynner med et linjestykke med lengde c (grunnlinjen i trekanten). Formelen for arealet blir dermed:

`h = (c * h)/(2)`

For elevene kan det se ut som om dette er en likning med to ukjente, c og h. Men her er det bare h som er ukjent, mens c er lengden til grunnlinjen i trekanten. Det kan være uvant for elevene.

Elevene får så en formel for høyden:

`h = (12 * 2)/(c)`

Hvis GeoGebra ikke tegner en sirkel, har elevene valgt for lang grunnlinje.

Deretter kan elevene konstruere trekanten på samme måte som i aktivitet 5. Resultatet blir en trekant med areal 12 og tre blå hjørner som elevene kan bevege fritt. Elevene kan gjerne vise at det blir riktig selv om de bruker mange desimaler på sidelengdene. Dette står i kontrast til aktivitet 1, der det var vanskelig å få til areal 12 når elevene valgte 2 eller flere desimaler.

Ekstra utfordring

Aktiviteten passer for elever som vil utforske GeoGebra litt ekstra, og læreren kan gi den til elever som blir tidlig ferdig eller trenger ekstra utfordring.

Oppgavetekst

Lag en figur der du kan endre både areal og grunnlinje. Det vil si at du skal klare å tegne en figur med areal 10 og grunnlinje 12, og deretter endre figuren til å ha areal 18 og grunnlinje 4.

Kommentarer til læreren

Her må elevene velge en variabel for grunnlinje og en variabel for areal. Den enkleste framgangsmåten er at elevene starter med å lage Glider for c og A. Resten av konstruksjonen er som før, bortsett fra at elevene erstatter 8 med c og 12 med A. Ved å bevege på gliderne kan elevene stille inn nøyaktig hvilken lengde og areal de ønsker (se figur 5).

Høyden til trekanten er gitt ved: `h = (2A)/(c)`, og det må elevene bruke når de skal lage sirkelen som bestemmer avstanden mellom grunnlinjen til trekanten og parallellen som høyden må ligge på (se figur 6).

Figur 5: Trekant hvor elevene kan endre på grunnlinje og areal med glidere.

Figur 6: Sirkel hvor radius er gitt av størrelsen på areal og grunnlinje.

Oppsummering

Målet med opplegget er å gi elevene en økt forståelse for geometriske sammenhenger. Ved å bruke algebra kan elevene komme fram til at sammenhengen mellom grunnlinje og høyde stemmer uansett lengden av grunnlinjen. GeoGebra gir elevene trening i bruk av dynamisk programvaren, og de blir kjent med fordeler og ulemper med digitale tegninger. At det er avgjørende å bruke den samme bokstaven bare en gang i hver tegning, tvinger elevene til en nøyaktighet som de ellers gjerne hopper over.