Treet – Følger, rekker og funksjoner
Hensikt
``Utforske ulike egenskaper til et mønster, lage generelle uttrykk og sjekke gyldigheten til løsningene.
Valg av tidspunkt
Du treng
PC med GeoGebra og elevark.
Aktiviteten
Elevene skal utforske et tre som forgrener seg etter et gitt mønster. Mønsteret er et godt utgangspunkt for å undersøke ulike rekker og følger. Elevene skal så lage generelle uttrykk som viser sammenhengen. Til ett av uttrykkene bruker de GeoGebra som hjelp.
Start med en klassesamtale slik at alle elevene forstår hvordan figuren er bygget opp.
Aktivitet 1
Målet med aktiviteten er at elevene skal bli kjent med mønsteret og forsøke å lage et generelt uttrykk for sammenhengen.
Oppgave fra elevark
Figuren er laget slik at grenene deler seg i to. Hver nye gren er halvparten så lang som den foran.
Tenk at dere lager uendelig mange grener.
- Fyll ut tabellen.
- Sammenlign løsningen deres med andre elevgrupper.
- Forklar hvordan dere har tenkt.
Kommentar til læreren
Elevene arbeider i par eller små grupper. Etter en stund skal de sammenligne resultatene med andre par/grupper og forklare hvordan de har tenkt. På den måten kan elevene sjekke egne resultater og unngå at for eksempel regnefeil ødelegger for det videre arbeidet. Det er ikke nødvendig at alle elevene har fylt ut hele tabellen før de sammenligner svarene og læreren inviterer til klassesamtale.
De fleste elever vil finne antall nye grener, lengden til en av de nye grenene og total lengde av alle grenene til sammen, når antall steg er et bestemt tall. Når de skal finne lengden fra rot til tupp kan det være lurt å tegne figuren så det blir lettere visualisere. Hvis elever strever, kan de fylle ut tabellen kolonne for kolonne istedenfor rad for rad. Da kan de følge samme tankegangen fra steg til steg.
I den siste raden skal elevene lage generelle uttrykk for steg n. Det vil være utfordrende for mange elever. Oppfordre de til å beskrive mønsteret med ord først så kan det bli lettere å lage et algebraisk uttrykk.
Å finne uttrykket for total lengde fra rot til en tupp er det mest utfordrende. Det er ikke nødvendig at elevene finner et generelt uttrykk før de starter på aktivitet 2. Der skal de bruke GeoGebra som støtte til å lage et uttrykk for sammenhengen.
| Steg | Antall nye grener | Lengden til en av de nye grenene | Total lengde til alle genene | Total lengde fra rot til tupp |
| 0 | 1 | `1` | `1` | `1` |
| 1 | 2 | `(1)/(2)` | `2` | `1 + (1)/(2) = (3)/(2)` |
| 2 | 4 | `(1)/(4)` | `3` | `1 + (1)/(2) +(1)/(4) = (7)/(4)` |
| 3 | 8 | `(1)/(8)` | `4` | `1 +(1)/(2) + (1)/(4) + (1)/(8) = (15)/(8)` |
| ... | ||||
| n | `2^(n)` | `(1)/(2^(n))` | `n+1` |
Det finnes flere strategier for å komme fram til et generelt uttrykk for lengden fra rot til en tupp. Noen elever vil oppdage at lengden fra rot til tupp alltid er 2 minus lengden til den siste nye grenen, uten å sette opp regnestykker. Elever som løser oppgaven med strategi 2 bruker det de har lært om potenser. De ser at oppgaven handler om potenser av 2. Elever som løser oppgaven med strategi 3 legger sammen brøkene og betrakter mønsteret i teller og nevner hver for seg.
| Steg | Strategi 1 | Strategi 2 | Strategi 3 |
| 0 | 2 minus lengden til den siste nye grenen | 1 | 1 |
| 1 | `1 + (1)/(2) = (3)/(2)= 2 - (1)/(2^(1))` | `1 + (1)/(2) = (3)/(2) = (4-1)/(2) = ((2^(n)-1)/2^(1))` | |
| 2 | `1 + (1)/(2) + (1)/(4) = (7)/(4) = 2 - (1)/4 = 2 - (1)/(2^(2)` | `1 + (1)/(2) + (1)/(4) = (7)/(4) = (8 -1)/4 = (2^(3) - 1)/(2^(2)` | |
| 3 | `1 + (1)/(2) + (1)/(4) + (1)/(8) = (15)/(8) = 2 - (1)/8 = 2 - (1)/(2^(3)` | `1 + (1)/(2) + (1)/(4) + (1)/(8) = (15)/(8) = (16 -1)/8 = (2^(4) - 1)/(2^(3)` | |
| ... | |||
| n | `2 - (1)/(2^(n))` | `(2^(n + 1) - 1)/(2^(n))` |
Hvis alle strategiene blir brukt i klassen, er det en god anledning til å repetere potensreglene for å vise at uttrykkene er riktige.
`(2^(n + 1) - 1)/(2^(n)) = 2^(n + 1)/(2^(n)) - 1/2^(n) = (2^(n)· 2)/(2^(n)) - 1/2^(n) = 2 - (1)/(2^(n))`
Aktivitet 2
Målet med aktiviteten er å lage et generelt uttrykk for total lengde fra rot til tupp med hjelp av GeoGebra.
Gi elevene oppgaven muntlig:
- Legg tallene fra Steg og fra Total lengde fra rot til tupp inn i regnearket i GeoGebra (steg 72 kan de utelate).
- Velg Lag liste med punkter.
- Lukk regnearket.
- Undersøk punktene i Grafikkfeltet.
- Lag en funksjon som passer til punktene.
Kommentar til læreren
Elevene er vant til å finne formler ved hjelp av regresjon i GeoGebra, men til denne oppgaven passer ingen av de forhåndsdefinerte funksjonene. I stedet skal elevene bruke de dynamiske egenskapene til GeoGebra som støtte når de resonnere seg fram til riktig uttrykk. Aktiviteten vil derfor også passe for elever som allerede har funnet det generelle uttrykket.
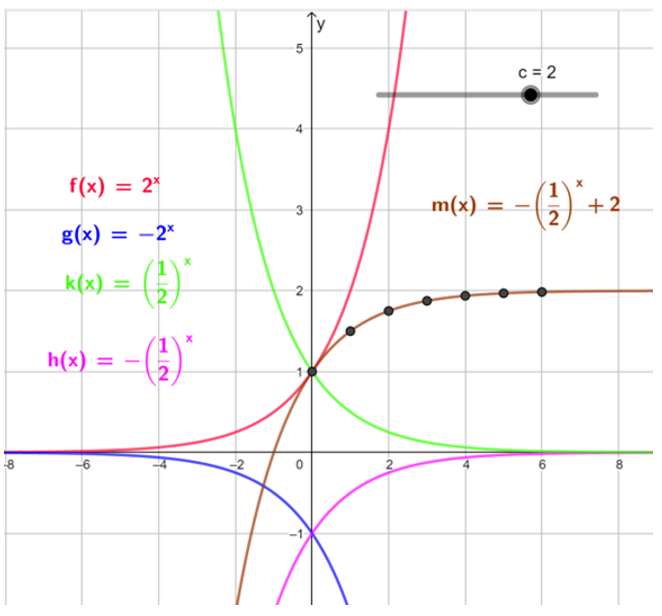
På bildet er det tatt utgangspunkt i f(x) = 2x. Elevene kan observere at grafen har en form som ligner, men at den har feil retning. Bildet viser mulige tilnærminger. Grafen h(x) har riktig form, men ligger for lavt i forhold til punktene. Elevene vet at ved å endre konstantantleddet kan de endre hvor grafen skjærer y-aksen. Hvis de lager en glider, kan de flytte grafen opp og ned langs y-aksen.

Gode spørsmål:
- Har dere sett en type graf som kan passe til punktene?
- Hvilke typer funksjoner går alltid gjennom punktet (0,1)?
- Tegn inn funksjonen `f(x) = 2^(x)` Hvordan passer den til punktene?
- Hvordan kan dere endre funksjonsuttrykket slik at grafen «bøyer seg» en annen vei?
- Hvordan kan dere flytte grafen langs y-aksen?
- Kan en glider hjelpe dere?
Noen elever synes at det vanskelig å finne generelle formler. GeoGebra kan gi disse elevene god støtte i arbeidet. I denne aktiviteten kan ikke elevene bruke en av de forhåndsdefinerte funksjonene i regresjonsanalysen, men de må bruke kunnskapene de har om funksjoner.
Vis fram ulike fremgangsmåter og drøft uttrykkene elevene har funnet i en klassesamtale. Oppfordre elevene til å sette ord på hvilke matematiske egenskaper de har brukt for å komme fram til et uttrykk som passer til punktene.
Aktivitet 3
Be elevene undersøke hva som skjer med grafen når n blir uendelig stor. Hvor langt blir det fra rot til tupp? Utfordre dem til å vise det på flere måter.
Kommentar til læreren
Observer hvilke metoder elevene bruker. Når elevene har funnet flere ulike løsninger, kan gruppene få vise fram og forklare hvordan de har tenkt. Det er viktig å få fram at det finnes mange muligheter for å finne en løsning på denne utfordringen. Elevene kan da oppdage at ulike kompetansemål henger sammen. For mange elever vil dette gi en aha-opplevelse som kan bidra til dybdelæring.
Grafisk løsning
Tegn grafen til uttrykket og velg Asymptote. Summen nærmer seg 2 hvis n blir uendelig stor.
Grenseverdi ved regning:
Dette er en god repetisjon av algebra. Utfordringen er å omforme 2n+1 slik at elevene kan forenkle brøken.
`lim_(n->oo)(2^(n+1)-1)/(2^(n)) = lim_(n->oo) ((2^(n+1))/2^(n) - (1)/(2^(n))) = lim_(n->oo) ((2·2^(n))/2^(n) - (1)/(2^(n))) = 2 - lim_(n->oo) (1)/2^(n) = 2`
Grenseverdi som sum av en uendelig geometrisk rekke
Lengden øker slik: `1 + (1)/(2) +(1)/(4) + (1)/(8) +(1)/(16)...`
Den totale lengden er en geometrisk rekke hvor `k = (1)/(2)` og `a_(1) = 1`.
`s = (a_(1))/(1-k) = (1)/(1- (1)/(2))= 2`
Rammeplanmål/Kompetansemål
- Videregående
- R2
- gi eksempler på ulike situasjoner som kan modelleres ved å bruke ulike matematiske funksjoner, og modellere og analysere slike situasjoner ved å bruke reelle datasett
- utforske egenskaper ved ulike rekker og gjøre rede for praktiske anvendelser av egenskaper ved rekker
- S2
- modellere og analysere eksponentiell og logistisk vekst i reelle datasett
- utforske egenskaper ved ulike rekker og gjøre rede for praktiske anvendelser av egenskaper ved rekker
- Vg1T
- formulere og løyse problem ved hjelp av algoritmisk tenking, ulike problemløysingsstrategiar, digitale verktøy og programmering
- modellere situasjonar knytte til ulike tema, drøftedrøfte, presentere og forklare resultata og argumentere for om modellane er gyldige


