Matematikk S2, Eksempeloppgave med CAS og sannsynlighetskalkulator

Del 2, oppgave 5

Oppgaven er hentet fra eksamen i REA3028 Matematikk S2, våren 2012 (s. 14).

PISA er en internasjonal undersøkelse som blir gjennomført hvert tredje år blant skoleelever i en rekke land. Ved undersøkelsen i 2009 var det med 4700 elever fra Norge. I naturfag scoret de norske elevene i gjennomsnitt 500 poeng. Det var nøyaktig likt det internasjonale gjennomsnittet. Standardavviket for norske elever var 90 poeng.

Vi trekker tilfeldig ut en elev blant de norske deltakerne. I oppgavene a) og b) kan du regne med at poengsummen til eleven er normalfordelt med forventningsverdi 500 poeng og standardavvik 90 poeng.

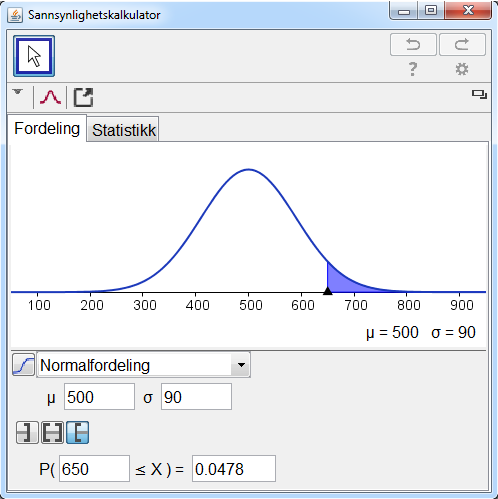
a) Bestem sannsynligheten for at eleven scoret minst 650 poeng.

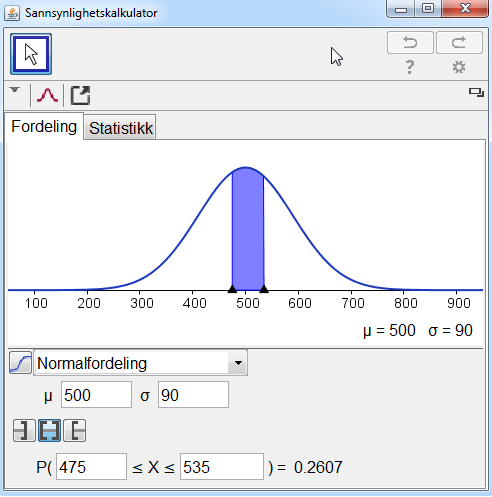
b) Bestem sannsynligheten for at eleven scoret mellom 475 og 535 poeng.

I virkeligheten kjenner vi ikke forventet poengsum for norske elever. Vi vet bare at gjennomsnittet var 500 poeng for de 4700 elevene som var med i undersøkelsen.

c) Er det grunnlag for å si at norske elever var bedre enn elever fra land som scoret 495 poeng? Velg signifikansnivå selv.

Løsningsforslag

a) Jeg skriver inn i sannsynlighetskalkulatoren og får sannsynligheten for at eleven scoret minst 650 poeng:

`P(X>=650) = 0,0478 ~~4,8%`

Sannsynligheten for at en elev fikk minst 650 poeng er 4,8 %.  

b) Jeg skriver inn i sannsynlighetskalkulatoren og får sannsynligheten for at eleven scoret mellom 475 og 535 poeng:

`P(475<=X<=535) = 0,2607 ~~26,1%`

Sannsynligheten for at en elev fikk mellom 475 og 535 poeng er 26,1 %.  

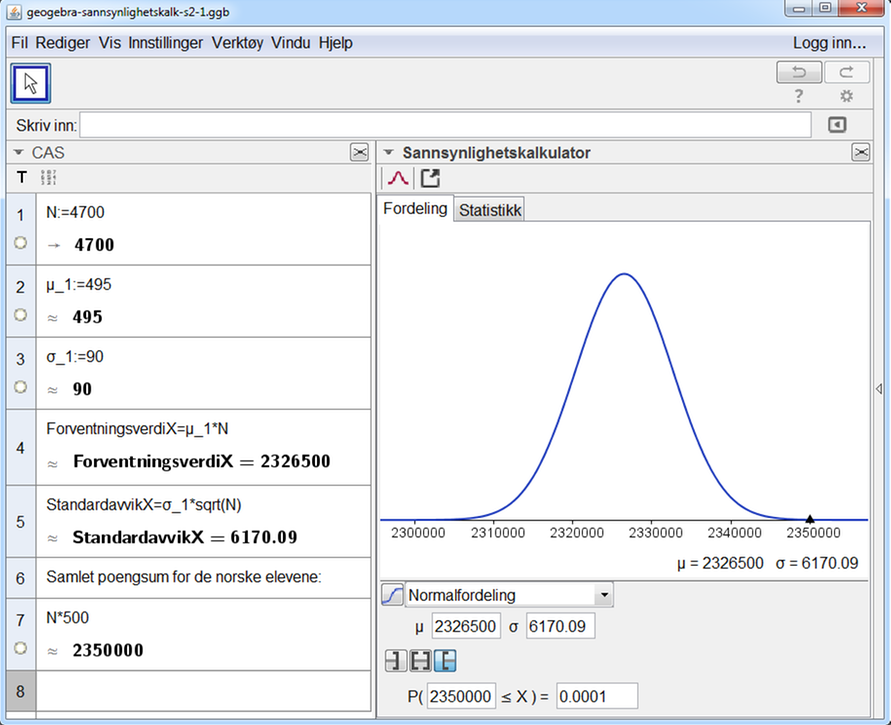
c) Jeg setter opp en nullhypotese, H₀: µ=495 og en alternativ hypotese H₁: µ>495. Jeg lar fortsatt standardavviket være 90 og velger 5 % som signifikansnivå. Jeg antar at nullhypotesen er sann.

Jeg må finne sannsynligheten for at det var tilfeldig at 4700 norske elever scoret (i gjennomsnitt) 500 poeng hver. 

Det er 0,0001 ≈ 0,01 % sannsynlighet for at resultatet til de norske elevene var tilfeldig, mye mindre enn 5 % (valgt signifikansnivå). Jeg kan derfor forkaste nullhypotesen og si at de norske elevene var bedre enn elever fra land som scoret 495 poeng.

Kommentarer

Det er ikke obligatorisk å kunne bruke sannsynlighetskalkulatoren på eksamen, men den vil være til stor hjelp dersom elevene skal løse sannsynlighetsoppgaver på del 2 på matematikkeksamen.