Rotasjon av likesida mangekantar

Kongruensavbildning, rotasjon, rotasjonssentrum, vinkel, rotasjonssymmetrisk, mangekanter, GeoGebra

Ein PC med GeoGebra og eit elevark til kvart par/kvar elevgruppe.

Aktivitet 1

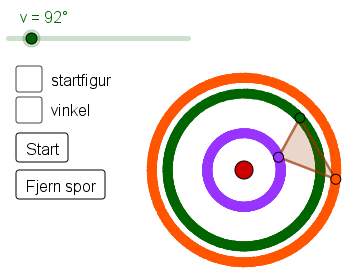
Elevane arbeider i par. De skal undersøke animasjonen Rotasjon som viser ein trekant som roterer om eit punkt. Animasjonen ligg på www.geogebra.org/u/matematikksenteret. Etter at elevane har arbeidd ei stund, fortset aktiviteten med ein klassesamtale med animasjonen på storskjerm. Da kan dei enkelt vise fram det de har funne ut.

Kommentarer til læraren

Det er mogeleg å bevege på glideren for å rotere trekanten samt rotere automatisk med start- og stoppknappen. Glidaren går frå 0° til 720°. GeoGebra kan vise originalen og rotasjonsvinkelen, i tillegg til den roterte trekanten. Det gjer det lett å sjå at 360° er ei heil omdreiing sidan den roterte trekanten dekker originalen. Ved å klikke på vinkel i animasjonen kjem to linjestykke mellom punkt på originalen, rotasjonssentrum og punkt på den roterte trekanten fram, i tillegg til vinkelen mellom linjestykka.

I animasjonen er det sett på sporing på hjørna slik at elevene kan følge bevegelsen til punkta. Ved å stoppe animasjonen, dra i eitt hjørne eller flytte heile trekanten og så starte animasjonen igjen fleire gongar, får elevane varierte erfaringar med rotasjon. Oppfordre dei til å undersøke kva som skjer når rotasjonssenteret er innafor, på og utanfor trekanten.

Når elevane har vorte kjente med animasjonen og fått nokre erfaringar, fortset aktiviteten med ein klassesamtale. Vektlegg rotasjon som kongruensavbildning (formen er den same etter rotasjon) og kva som skjer med hjørna til trekanten under rotasjonen. Bruk relevante omgrep som rotasjon, rotasjonssentrum og rotasjonsvinkel.

Gode spørsmål til oppsummering:

• Kvifor teiknar GeoGebra sirklar?
• Kva betyr tala på glideren?
• Kor ligg trekanten dersom glidaren står på 90° eller 180°?
• Kor ligg trekanten når ein roterer med 360°, 540° eller 720°?
• Kor er vinkelen GeoGebra måler?
• Vinkelen (i trekanten) veks i takt med glidaren, men startar på nytt etter 360°. Kvifor gjer han det?

Vinklane 360°, 540° eller 720° er godt kjente for elevar som likar snowboard eller skateboard, noko som gjer det lettere å knytte rotasjon til noko die kan frå før.

Aktivitet 2

Elevane skal no utforske likesida mangekantar. I felles klasse lagar dei den første teikninga (konstruksjonen) dei skal arbeide med i GeoGebra, nemleg ein sekskant som dei kan rotere med glidar. Instruksjonen står også på elevarket dersom elevane gløymer framgangsmåten når dei skal lage dei andre mangekantane.

Forslag til framgangsmåte: 

• Åpne ei ny fil i GeoGebra.
• Skjul aksar og rutenett.
• Lag ein glidar for rotasjonsvinkelen:
  • Vel Glider og trykk i Grafikkfeltet.
  • Vel Vinkel.
  • Slett α = 45° og skriv v.
  • Trykk OK.
• Teikn ein likesida sekskant.
• Teikn eit punkt som skal vere rotasjonssentrum.
• Vel Roter objekt om punkt med fast vinkel.
• Trykk på sekskanten og på punktet (rotasjonssenteret) og skriv v som vinkel.

Elevane fortset så å arbeide i par med elevarket. Målet er å finne ut kor mange grader dei må rotere ulike likesida mangekantar for å få den roterte mangekanten til å dekke originalen.

Kommentarer til læreren

I aktivitet 1 oppdaga elevane at den roterte trekanten alltid dekka originalen når dei roterte 360°, men er det mogeleg å rotere med ein mindre vinkel? I denne aktiviteten vil elevane oppdage at det er mogeleg for likesida mangekanter, og at plasseringa av rotasjonssenteret er avgjerande.

Elevane startar med å lage ein likesidet sekskant som dei kan rotere med ein glidar. Likesida mangekant heiter Regulær mangekant i GeoGebra. Ettersom dette er ei ganske komplisert teikning for elevar på mellomtrinnet, anbefaler vi å gjere dette i felles klasse. På den måten kjem alle godt i gang, og kan deretter fortsetje utforskinga i par. Oppfordre dei til å bevege på glidar og rotasjonssenteret og observere kva som skjer før dei begynner med oppgåvene på elevarket.

Elevane må sjølv finne ut at midtpunktet til mangekanten må vere rotasjonssenteret. Når dei har arbeidd ei stund med aktiviteten, er det lurt med ein klassesamtale med fokus på denne matematiske samanhengen slik at elevane kan starte med å finne midtpunktet til mangekantane i den videre utforskinga.

Dei tre første oppgåvene er rotasjon av ein likesida sekskant, eit kvadrat og ein likesida trekant. Rekkefølga på oppgåvene er bevisst vald ut. Elevane ser samanhengen med vinklar betre i ein sekskant enn i ein trekant. Dersom elevane brukar linjer/linjestykke for å finne midtpunktet, er det enklare å finne midtpunktet i mangekantar der talet på sider er eit partal enn eit oddetal. Så det å starte med for eksempel ein femkant kan øydelegge noko av eksperimenteringa. Nokre elevar vil oppdage at GeoGebra kan finne midtpunktet for de dersom dei brukar Midtpunkt eller sentrum algebra. 

Oppfordre elevane til å leite vidare når dei har funne ei løysning og til å resonnere over om dei har funnet alle løysningane. Elevane skal så undersøke likesida mangekantar dei velg sjølv. Kan dei finne ein generell regel som gjeld for alle likesida mangekantar når rotasjonssenteret er plassert i midten av mangekanten? Mange elevar vil oppdage at dersom dei deler 360˚ på antal sider så får dei ein vinkel de kan rotere med for å dekke originalen. Nokre vil også oppdage at dei kan rotere med multiplum av denne vinkelen.

Gi elevane nok tid til å prøve (og å feile). Jo meir elevane får prøve sjølv, jo betre blir dei til å bruke GeoGebra. Det digitale verktyet hjelper elevane med å utvide forståinga av geometri, og dei opplever også opplæringa i det digitale verktøyet som relevant når ho skjer samstundes som dei arbeider med matematiske problem.

Observer korleis elevane angrip problemet. Tenkjer elevane før dei velg ein verdi for vinkelen, eller prøver dei seg berre fram? I motsetning til konstruksjonar på papir gjer GeoGebra det mogeleg å teikne alle mogelege regulære mangekantar og velje alle mogelege vinkelstorleikar. Elevane ser med ein gong om løysinga stemmer. Angre-knappen gjer det lett å prøve på nytt dersom resultatet ikkje blir som forventa.

Oppsummering

Som oppsummering skal elevane vise fram korleis dei har tenkt, og ulike matematiske sammenhenger dei har funne. Vel ut elevane som skal presentere arbeidet sitt basert på observasjonane undervegs, og pass på at klassen får sjå ulike løysingsmetodar.