Hva er modellering?

Verden vi lever i kan være uoversiktlig og kompleks. Ofte trenger vi å forenkle problemer og situasjoner som oppstår, og da kan vi bruke matematikk. Modellering handler om å løse problemer fra den virkelige verdenen. Å beskrive virkeligheten med matematisk språk kalles en matematisk modell. En matematisk modell er altså en forenkling av den komplekse og uoversiktlige virkelige verdenen.

«En modell i matematikk er en beskrivelse av virkeligheten i matematisk språk. Modeller i matematikk brukes for å beskrive fenomener i dagliglivet, arbeidslivet og samfunnet ellers.»

- Utdanningsdirektoratet

Når elevene arbeider med modellering i matematikk, arbeider de med et problem fra den virkelige verdenen. De må forstå, forenkle og oversette problemet til den matematiske verdenen. I den matematiske verdenen løser elevene problemet og går tilbake til den virkelige verdenen for å vurdere om løsningen er gyldig. Modellering er å arbeide i begge de to verdenene (den virkelige og den matematiske), og å bevege seg mellom dem.

Elever er vant til å møte oppgaver med gitte fremgangsmåter der alle opplysninger er tilgjengelige. Derfor er det krevende å løse problemer der de selv må gjøre antagelser og avgrensninger, finne informasjon og velge fremgangsmåter. Dette krever at elevene får mulighet og tilstrekkelig tid til å øve på og arbeide med matematisk modellering. Elevene trenger også øving i å validere fremgangsmåtene de velger, og svarene de kommer frem til. De må kunne vurdere og argumentere for at løsningen kan være gyldig for det virkelige problemet.

Modelleringsprosessen

Ferri (2018), Maaß, (2006), Blum og Leiss (2007) har laget en visualisering av modelleringsprosessen. Ved å ta utgangspunkt i denne og den helhetlige problemløsningsmodellen (Matematikksenteret, u.å.), har vi laget en representasjon som passer godt i norske klasserom (se figur 1).

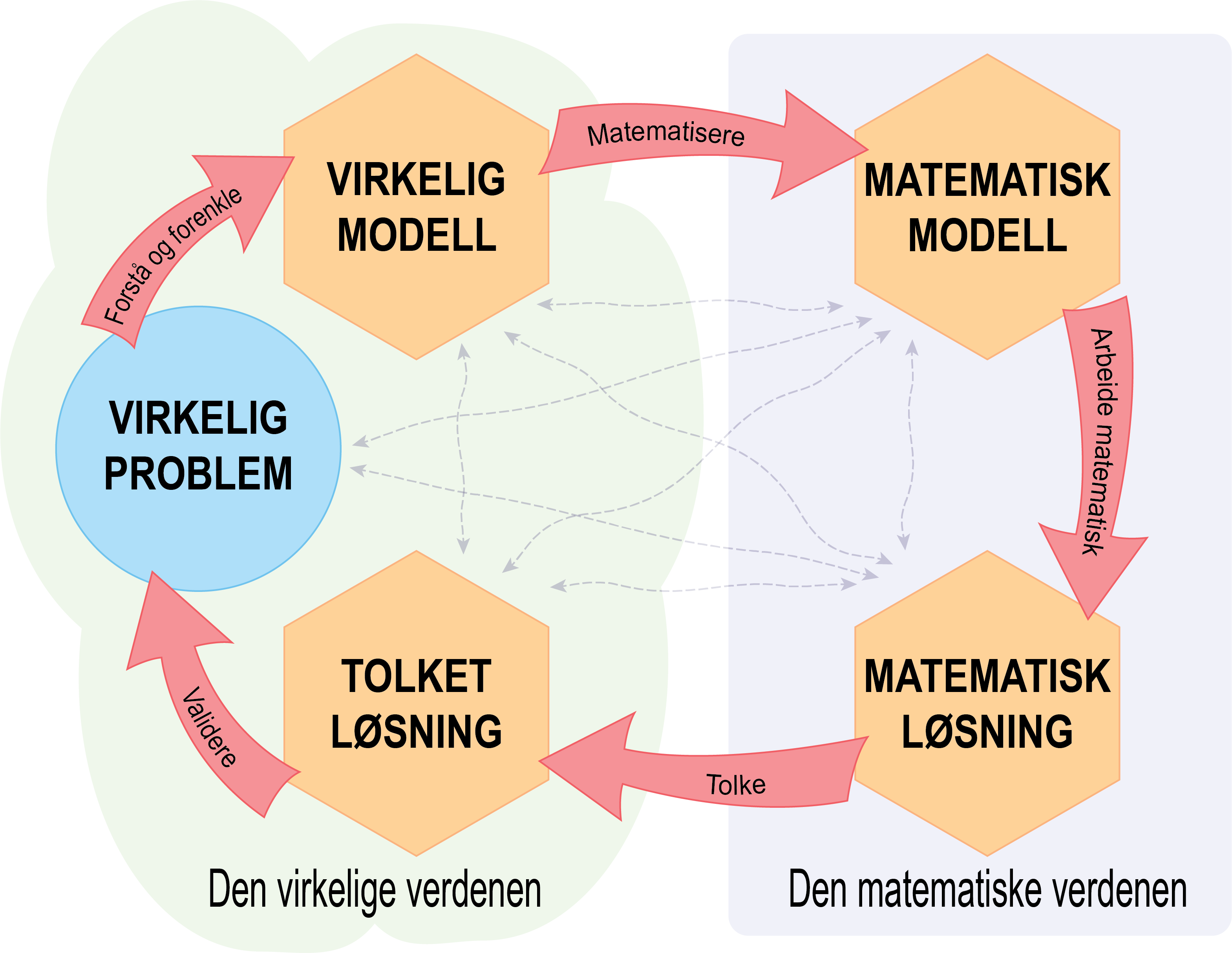
Figur 1 viser sammenhengen mellom den virkelige verdenen og den matematiske verdenen i modelleringsprosessen. De røde pilene viser det elevene må gjøre, og sekskantene illustrerer steg de kommer til i prosessen.

Modelleringsprosessen starter med et problem fra den virkelige verdenen. Elevene må forstå og forenkle problemet. Det vil si at de må ta valg og gjøre antakelser for at de skal kunne håndtere problemet og lage en virkelig modell. Når elevene tallfester den virkelige modellen, kalles det "å matematisere". Den matematiske modellen kan for eksempel bestå av tekst, tall, tabeller og/eller tegninger. Deretter arbeider elevene matematisk ved å gjøre beregningene de trenger for å komme frem til en matematisk løsning. De må tolke den matematiske løsningen opp mot det virkelige problemet. Det innebærer å oversette den matematiske løsningen tilbake til den virkelige verdenen. I siste fase i prosessen må elevene validere løsningen sin. De må vurdere om løsningen sin kan være en løsning på det virkelige problemet. Det virkelige problemet er både start- og endepunkt i modelleringsprosessen.

Selv om representasjonen kan oppleves som enkel og lineær, er modelleringsprosessen uoversiktlig. Det er ikke slik at elevene beveger seg fra punkt til punkt i en slik prosess, men frem og tilbake (Ferri, 2018). Figur 1 viser dette med de små, grå pilene. Elevene kan med andre ord bevege seg mellom den matematiske verdenen og den virkelige verdenen flere ganger i samme problem.

Utskriftsvennlig poster av modelleringsmodellen (pdf)

Hvorfor arbeide med modellering?

Det er mange grunner til at elevene bør utvikle modelleringskompetanse. Steffensen (2023) har i sin bok «Modellering - matematikk for skole og samfunn» en rekke begrunnelser for hvorfor det er viktig å inkludere matematisk modellering i skolen:

Figur 2: Begrunnelser for modellering i skolen (Steffensen, 2023, s. 19).

	Øke elevers forståelse av sentrale aspekter ved verden (dagligliv, samfunn etc.)		Gjøre slik at elever kan bruke matematikk i sitt hverdagsliv og senere yrkesliv		Gi rike læringsmuligheter, som bidrar til utvikling av begrep, kommunikasjon og validering av resultat
	Gi elever mulighet til kritisk å vurdere matematisk informasjon – og slik gjøre dem til aktive borgere i samfunnet		Fostre og øke elevers motivasjon og holdning til matematikk		Introdusere nye matematiske begrep og prosedyrer, og strukturere elevenes læringsprosesser
	Modeller kan brukes til å eksemplifisere begrep og prosedyrer		Gi et mer realistisk bilde av matematikk og gi innsikt i hvordan matematikk overlapper med andre fagområder		Bidra til kritisk dømmekraft over oppstilling og anvendelse av matematiske modeller

Det er vanskelig å forutse hvilke yrker elevene våre kommer til å ha i fremtiden. Mange vil sannsynligvis jobbe i yrker som vi i dag ikke kjenner behovet for. Å sette seg inn i nye og ukjente utfordringer vil derfor være en viktig kompetanse elevene trenger i sitt yrkesliv. Verdenssamfunnet står overfor store og vanskelige utfordringer. Både klimautfordringer og knapphet på ressurser er utfordringer som elevene vil møte i fremtiden. Å løse disse utfordringene, men også å kunne mene noe om dem, kommer til å kreve modelleringskompetanse.