Modellering i skolen

Modellering i læreplanen

Modellering i matematikk har en sentral rolle i LK20.  Begrepet modellering er nevnt blant annet i kjerneelementene, i et tverrfaglig tema og i kompetansemål for spesifikke trinn.

Kjerneelementene viser det mest betydningsfulle faglige innholdet som elevene skal arbeide med i opplæringen, og de skal prege innholdet og progresjonen i undervisningen. (Utdanningsdirektoratet, u.å.). Det betyr at elevene bør arbeide med modellering gjennom hele skoleløpet. I kjerneelementet «Modellering og anvendelser» kommer det tydelig frem at elevene skal arbeide med problemer fra den virkelige verdenen:

En modell i matematikk er en beskrivelse av virkeligheten i matematisk språk. Elevene skal ha innsikt i hvordan modeller i matematikk brukes for å beskrive dagliglivet, arbeidslivet og samfunnet ellers. Modellering i matematikk handler om å lage slike modeller. Det handler også om å kritisk vurdere om modellene er gyldige, og hvilke begrensninger de har, vurdere modellene i lys av de opprinnelige situasjonene og vurdere om de kan brukes i andre situasjoner. Anvendelser i matematikk handler om at elevene skal få innsikt i hvordan de skal bruke matematikk i ulike situasjoner, både i og utenfor faget.

- Utdanningsdirektoratet, u.å.

Modellering er også nevnt i kjerneelementet «Matematiske kunnskapsområder» og i det tverrfaglige temaet «Folkehelse og livsmestring».

Modellering er spesifikt nevnt i kompetansemål etter 4. og 10. trinn, og i underveisvurdering for 8. trinn. Læreplanen for VGS (1P, 2P, 1T, S1, S2, R1 og R2) inneholder også kompetansemål som omtaler modellering.

Det er verdt å merke seg at trinn som ikke har ordet modellering i sine kompetansemål, likevel skal arbeide med kjerneelementene, og dermed med modellering.

Modelleringsoppgaver

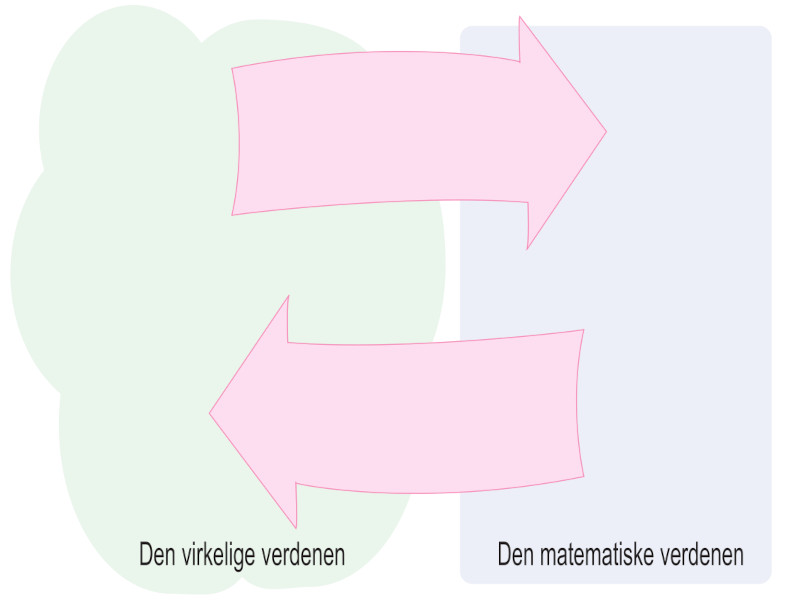
I modelleringsoppgaver får elevene et problem fra den virkelige verdenen. Elevene må bevege seg mellom den virkelige verdenen og den matematiske verdenen for å kunne løse problemet. Problemet mangler ofte opplysninger og har sjeldent ett riktig svar. Løsningen avhenger av hvilke valg og antakelser elevene har tatt.

Å velge ut gode modelleringsoppgaver kan være utfordrende. Ferri (2018) presenterer noen kriterier som det kan være fint å ta utgangspunkt i. En god modelleringsoppgave er:

• et problem, altså har ikke elevene en kjent løsningsmetode.
• åpen, altså kan elevene løse den på ulike måter.
• kompleks, altså mangler den opplysninger og elevene må selv avgjøre hvilke opplysninger de trenger.
• realistisk, altså skal elevene ta utgangspunkt i den virkelige verdenen.
• autentisk, altså skal ikke oppgaven være oppkonstruert kun for å regne matematikk i en pseudovirkelighet.
• løsbar gjennom modelleringsprosessen.

Lærerens rolle

Det kan være nyttig å ha noen holdepunkter når du planlegger en økt med modellering. Her er noen prinsipper som er viktige i planleggingen og i gjennomføringen av en modelleringsøkt, inspirert av Ferri (2018).

1. Målet for økta

Du bør være bevisst hva målet for økta skal være. Skal målet være å øve på hele eller deler av modelleringsprosessen? Eller er målet å bruke modellering til å styrke forståelse av en matematisk idé?

2. Valg av modelleringsoppgave

Velg en modelleringsoppgave som er relevant for dine elever. Temaet kan være noe som interesserer dem akkurat nå (Taylor Swift, Liverpool etc.), noe som er aktuelt for elevene i nærmiljøet (en severdighet, et turområde etc.) eller noe elevene bør kunne forholde seg til (økonomi, samfunnsspørsmål etc.).

3. Løs modelleringsoppgaven selv

Løs oppgaven selv ved å gå gjennom alle stegene i modelleringsprosessen. Skriv ned mulige løsninger elevene kan komme frem til. Tenk gjennom hvor de kan støte på problemer og hvordan du kan hjelpe dem videre. Lag gjerne åpne spørsmål knyttet til de ulike fasene i modelleringsprosessen, for eksempel «Hvilke opplysninger har vi?», «Hva mer trenger vi å vite?».

4. Organisering

Planlegg hvordan du vil introdusere oppgaven. Introduksjonen bør være kort, med åpning for oppklarende spørsmål. Husk at det er elevene som skal ta valg og gjøre avgrensninger, det er ikke din oppgave. Når elevene skal arbeide med oppgaven, bør de arbeide i små grupper. De bør også få beskjed om hvordan de skal presentere løsningen sin. Sett av nok tid til en oppsummeringssamtale.

5. I løpet av økta

Modellering kan være kognitivt krevende for elevene og de trenger øvelse i alle faser i modelleringsprosessen. Du skal støtte elevene i prosessen, men det er elevene som skal forstå og forenkle problemet ved å ta egne valg og antakelser. Det er derfor viktig at elevene får tid til å tenke selv før du kommer med hint eller spørsmål. Noen elever trenger bare et hint som «Les oppgaven en gang til», mens andre elever kan trenger mer direkte spørsmål som «Hvilke opplysninger mangler?», eller mer spesifikk hjelp som «Hvor lang er en bil?».

Gå rundt til alle gruppene og ta notater. Legg merke til ulike modeller og løsningsstrategier. Velg ut grupper som skal presentere arbeidet sitt, slik at du får frem ulike modeller og løsninger i oppsummeringssamtalen.

6. Oppsummering

La gruppene vise frem ulike modeller og løsninger de har kommet frem til. Det er viktig å la elevene få samtale om hvorfor gruppene har kommet frem til ulike løsninger. Husk at ulike valg og antakelser som er tatt gir ulike modeller, som igjen gir ulike løsninger.

Elevens rolle

Når elever arbeider med modelleringsoppgaver, vil spesielt starten være krevende (Ferri, 2018). Det er fordi opplysninger de trenger for å løse oppgaven, ikke er gitt. Det er verdt å merke seg at elevenes egne oppfatninger av hva de skal gjøre når de arbeider med en matematikkoppgave, kan være til hinder, til tross for at oppgaven ikke er for komplisert eller matematisk krevende (Nordskog, 2024). Et eksempel er elever som forventer å få en løsningsmetode fra lærebok eller lærer, før de så skal bruke den til å løse en oppgave. Modellering blir da utfordrende fordi elevene selv er nødt til å finne en metode.

Å gjøre elevene bevisste på at de arbeider med modelleringsoppgaver, kan føre til at de forstår at de må tilnærme seg problemet på en annen måte. Det kan også føre til at elevene forstår hvilken kompetanse de trenger når de arbeider med modellering.

Det er ikke nødvendig å gjøre elevene kjent med modelleringsprosessen i detalj. Etter at de har fått erfaring med modellering, kan det imidlertid være nyttig å bevisstgjøre elevene på de viktigste fasene i prosessen og å kreve at de kan redegjøre for dem i arbeidet sitt. Det kan føre til at det blir lettere for elevene å vite hvordan de skal angripe en modelleringsoppgave. Her er fire punkter elevene kan forholde seg til (Blum & Ferri, 2009):

1. Forstå problemet
   • Les teksten godt og se for deg situasjonen.
   • Lag en skisse.
2. Lag en modell
   • Finn informasjon du trenger. Om nødvendig, gjør antakelser.
   • Se etter matematiske sammenhenger (finn ut hvilken matematikk du trenger).
3. Bruk matematikk
   • Gjør beregninger.
   • Skriv ned det matematiske resultatet.
4. Forklar løsningen
   • Gjør rede for valg og antakelser.
   • Knytt svaret til oppgaven. Hvis nødvendig, gå tilbake til punkt 1.
   • Kan svaret du har fått være et svar på det opprinnelige problemet?

En annen måte å bevisstgjøre elevene på de ulike delene av modelleringsprosessen er å bruke Madsen og Eriksen (2024) sin tomme modelleringssyklus. Den er en forenklet versjon av modelleringsprosessen med fire områder: den virkelige verdenen, den matematiske verdenen og de to overgangene mellom disse. Underveis i prosessen kan du stoppe elevenes arbeid, og la de reflektere over hva de gjør og notere hvor det hører hjemme i den tomme modelleringssyklusen.