Kom i gang med modellering
Første modelleringsoppgave
Når elevene skal arbeide med en modelleringsoppgave for første gang, kan det være greit å bruke en oppgave som ikke er for omfattende og som er løsbar i løpet av en skoletime. Da er det mer sannsynlig at elevene får erfare hele modelleringsprosessen. Husk å gi elevene god tid til å dele erfaringene med oppgaven og modelleringsprosessen i klassen etterpå.
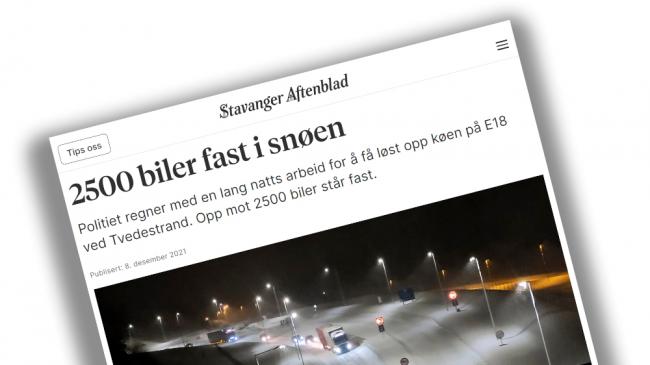
«Bilkø i snø»
Forslag til framgangsmåte med oppgaven Bilkø i snø:
Målet for økta
Første gang elevene skal arbeide med en modelleringsoppgave bør målet for økta være at de skal erfare alle delene i modelleringsprosessen.
Valg av oppgave
Temaet i oppgaven «Bilkø i snø» er kjent for elevene og mange av dem vil ha relevant kunnskap om typer kjøretøy, lengden til kjøretøy og lignende. Dette er spesielt viktig i den første og siste fasen i modelleringsprosessen.
Oppgaven «Bilkø i snø» er ikke så omfattende og elevene vil raskt forstå hva oppgaven handler om. Den har lav inngangsterskel. Samtidig gir oppgaven elevene gode muligheter til å gjennomføre flere runder i modelleringsprosessen. For eksempel kan det være elevgrupper som bare tar hensyn til lengden på kjøretøyene i modelleringsprosessen, men som i valideringsfasen kommer på at kjøretøyene ikke står tett i tett. Ettersom det er et mellomrom mellom kjøretøyene, må de gå tilbake og endre den virkelige modellen sin.
Løs oppgaven
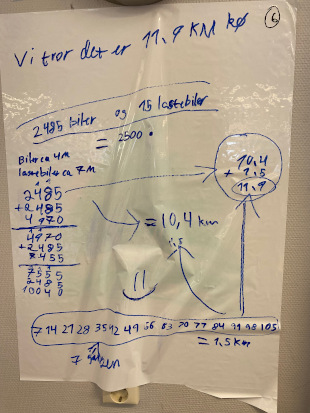
Før elevene skal løse oppgaven, må du som lærer løse oppgaven. Tenk gjennom hva du gjør og knytt det til de ulike delene i modelleringsprosessen. Hvor kan elevene møte utfordringer, og hvordan vil du hjelpe elevene videre? Erfaringene du får er svært nyttige når du skal støtte elevene i prosessen og når du skal velge ut eksempler på elevarbeid til oppsummeringen.
- Problemet i oppgaven hører til i den virkelige verdenen.
- Når du tar valg og antakelser om hvilke kjøretøy som er i køen, arbeider du med å forstå og forenkle problemet.
- Når du har en oversikt over de kjøretøyene du mener er i køen, har du laget en virkelig modell.
- Når du antar lengder til de ulike kjøretøyene, så matematiserer du problemet.
- Når du har en oversikt som viser antall av hvert kjøretøy og lengde til de ulike kjøretøyene, har du en matematisk modell av problemet.
- Når du multipliserer antall kjøretøy med den antatte lengden til kjøretøyene og legger disse sammen, så arbeider du matematisk.
- Tallsvaret du regner deg fram til, er din matematiske løsning.
- Når du knytter dette tallsvaret til den totale lengden på køen i oppgaven, tolker du din matematiske løsning.
- Når du ser på hva din løsning betyr for problemet, for eksempel at denne køen må ha strukket seg fra Tvedestrand til et nærliggende sted, så ser du på din tolkede løsning av problemet.
- Til slutt kan du vurdere om køen virkelig kunne ha vært så lang, og da validerer du løsningen opp mot den virkelige verdenen og det virkelige problemet.
Organisering
Vis oppgaven og les den høyt. Gi rom for oppklarende spørsmål, men husk at det er elevene selv som skal ta valg og gjøre antakelser for å lage sin egen modell.
Vi anbefaler at elevene arbeider i små grupper.
Det kan være en fordel å bruke vertikale tavler, for eksempel selvheftende whiteboardfilm. De gjør det blant annet lettere for deg som lærer å få en oversikt over elevens arbeid underveis, og gjør arbeidet synlig for hele gruppa. Det gir også grupper som står fast mulighet til å få støtte fra tavlene til de andre gruppene.
I løpet av økta
Gå rundt og skaff deg en oversikt over valg, antakelser og strategier. Hvis grupper trenger støtte, bør du stille åpne spørsmål (spørsmål som ikke har et fasitsvar). For eksempel: Hvilke opplysninger mangler? Hvordan har dere tenkt? Hvilke kjøretøy tror dere er i køen? Hvor lang er en bil? Hvor stor avstand er det mellom bilene når de står i kø?
Hvor direkte spørsmålene bør være er avhengig av gruppenes behov. Men husk å la elevene få tid og mulighet til å tenke selv.
Ofte stopper elevene når de har en matematisk løsning. De validerer sjelden løsningen sin opp mot det virkelige problemet (Utdanningsdirektoratet, 2014). Da må du stille spørsmål som leder elevene tilbake til det virkelige problemet. Eksempel: «Dere har kommet frem til at køen er 14 m lang. Hvor langt er det? Kan det stemme?» Oppfordre elevene til å sammenligne med en strekning de kjenner til.
Oppsummering
Velg ut grupper med ulike modeller og løsninger. Hvorfor har gruppene fått ulike svar? Det er viktig at elevene begrunner valg og antakelser de har gjort.
Eksempler på elevløsninger
Klassesamtale om modelleringsprosessen og veien videre
Etter dette første møtet med en modelleringsoppgave kan du ha en klassesamtale om oppgaven, der fokuset er på den første fasen i modelleringsprosessen. Elevene er ikke erfarne med denne type oppgave og det kan derfor være lurt å reflektere rundt noen av erfaringene de fikk.
Sammenligne oppgaver
La elevene reflektere over likheter og forskjeller mellom en lukket tekstoppgave og en modelleringsoppgave. Du kan for eksempel ta utgangspunkt i «Bilkø i snø» og denne tekstoppgaven:
| Kjøretøy | Lengde | Antall |
|---|---|---|
| Personbil | 4 m | 2000 |
| Lastebil | 12 m | 200 |
| Buss | 16 m | 100 |
| Varebil | 8 m | 50 |
| Bil m/henger | 8 m | 50 |
På E6 sto 2500 kjøretøy i kø. I tabellen er en oversikt over kjøretøyene som sto i denne køen. I tillegg var det 2 m mellom hvert kjøretøy. Hvor lang var køen?
Utfordre elevene til å finne likheter og forskjeller mellom oppgavene, men ha mest fokus på forskjellene. De fleste elevene vil oppdage at i tekstoppgaven er alle opplysninger gitt, mens i modelleringsoppgaven måtte de ta egne valg og gjøre egne antakelser. Få elevene til å sette ord på hva de måtte bestemme selv. For eksempel hvilke kjøretøy som var i køen, hvor lange kjøretøyene var og hvor stor plass det var mellom kjøretøyene. Et av kjennetegnene ved modellering er at elevene selv skal gjøre antakelser og i noen tilfeller hente inn opplysninger for å løse oppgaven. Gjør elevene bevisste på dette ved å løfte det frem i samtalen.
La elevene dele erfaringer om hvordan de opplevde modelleringsprosessen i arbeidet med «Bilkø i snø». Noen synes kanskje det var vanskelig å komme i gang og noen ble kanskje frustrerte. Andre synes kanskje det var artig at de kunne bestemme mye i oppgaven selv. Ved å dele disse erfaringene, vil de være mer forberedte til neste gang de skal arbeide med en modelleringsoppgave.
Elevene bør arbeide med flere modelleringsoppgaver slik at de får erfaring med hele modelleringsprosessen. Deretter kan du, sammen med elevene, utarbeide en oversikt over hvilke steg prosessen består av. En slik oversikt kan være en utfylt versjon av Eriksen og Madsen (2024) sin tomme modelleringssyklus, eller den kan ligne de fire punktene fra Blum & Ferri (2009):
-
Forstå problemet
-
Lag en modell
-
Bruk matematikk
-
Forklar løsningen
Det kan du lese mer om i Modellering i skolen.
Tips til flere modelleringsoppgaver.
Kilder
Blum, W., & Borromeo Ferri, R. (2009). Mathematical modelling: Can it be taught and learnt. Journal of mathematical modelling and application, (s. 45-58.).
Eriksen, S. og Madsen, J. (2024). Den tomme modelleringssyklusen. Tangenten, 35(2), 15-22.
Utdanningsdirektoratet (2014). Nasjonale prøver i regning – Veiledning til lærere – Regning 8. og 9. trinn. DEL 2. Utdanningsdirektoratet.