Jo større nevner (eller teller), jo større brøk
Når elever skal avgjøre størrelsen til brøker er det noen som overgeneraliserer kunnskapen de har om de naturlige tallene og desimaltall.
%2C%20jo%20st%C3%B8rre%20br%C3%B8k.png)
Heltallstenkingen medfører at elevene ser på teller og nevner som rene tallstørrelser uten å ta hensyn til forholdet mellom dem. Figuren til høyre viser eksempel på elevsvar der eleven mener at `(1)/(9)` er større enn `(1)/(8)` fordi 9 er større enn 8. I andre oppgaver vil noen elever svare at for eksempel `(9)/(12)` er større enn `(8)/(10)` fordi både teller og nevner er størst i `(9)/(12)`.
I desimaltall er 0,9 nærmere 1 enn 0,8. Noen elever overfører dette til brøk, og tenker at `(1)/(9)` er større enn `(1)/(8)`, og argumenterer med at `(1)/(9)` er nærmest en hel. På samme måte vurderer en del elever størrelsen til brøken `(1)/(5)`til å være omtrent en halv, altså at `(1)/(5)` er lik 0,5.
Noen elever betrakter brøkstreken som komma og vil si at `(1)/(9)` er større enn `(1)/(8)` fordi 1,9 er større enn 1,8. Mer om denne misoppfatningen omtales under brøkstrek er lik desimalkomma.
En annen misoppfatning er når eleven tar utgangspunkt i en hel, og vurderer størrelsen på brøken ut fra differensen mellom teller og nevner. Eksempel: `(2)/(3)` er større enn `(3)/(5)` fordi i `(2)/(3)` mangler det bare 1 i telleren for å få en hel, mens i `(3)/(5)` mangler det 2 i telleren for å få en hel. Som eksemplet viser blir svaret noen ganger riktig når elevene tenker på denne måten, men argumentasjonen avslører en misoppfatning. Misoppfatningen beskrives også under differensen mellom teller og nevner avgjør størrelsen på brøken.
En del elever pugger setningen «Jo større nevner, jo mindre brøk» som en regel. Oppfølgingsspørsmål vil avdekke om elevene forstår hvorfor det er slik.
Oppgaver
I prøven Misoppfatninger knyttet til brøk og prosent for 5.–7. trinn, er det seks oppgaver som tester misoppfatningen jo større nevner, jo mindre brøk, mens det er fem oppgaver i prøven for 8.–10. trinn som tester det samme. Tre av dem ser du nedenfor.
Analyse
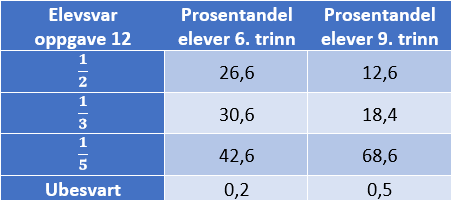
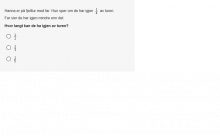
I oppgave 12 skal elevene velge hvilken av brøkene `(1)/(2)`, `(1)/(3)` eller `(1)/(5)`som er mindre enn `(1)/(4)`.Elever som er i misoppfatningen at større nevner gir større verdi, vil her svare `(1)/(2)`eller `(1)/(3)`. Resultatet av analysene viser at det gjelder godt over halvparten av elevene på 6. trinn og litt over 30 % av elevene på 9. trinn.
I oppgave 29 på 5.–7. trinn og oppgave 18 på 8.–10. trinn skal elevenes svar være en brøk som har dobbel så stor verdi som `(1)/(3)`. På 6. trinn svarer 65 % av elevene enten `(1)/(6)` eller `(2)/(6)`, og tilsvarende tall på 9. trinn er 56 %. 68 % av elevene som svarte feil i oppgave 12, svarte også feil i oppgave 29 i prøven for 5.–7. trinn og oppgave 18 i prøven for 8.–10. trinn.
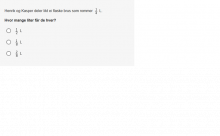
Elevene som er i misoppfatningen at større nevner gir større verdi, har også en misoppfatning om at mindre nevner gir mindre verdi. Dette tester blant annet oppgave 7 i prøven for 8.–10. trinn, der elevene skal finne ut hvor mye brus to gutter får hver, hvis de deler ei flaske som rommer `(1)/(4)` L brus likt. 50 % av elevene som svarte at det dobbelte av `(1)/(3)` er `(1)/(6)`, svarte at halvparten av `(1)/(4)` er `(1)/(2)`.
Elevsvar
Nedenfor er noen elevsvar fra da oppgavene ovenfor ble testet ut på papir, uten svaralternativer. Svarene er gitt av elever fra 5. til 10. trinn.
