Tar ikke hensyn til helheten
En grunnleggende forståelse av brøk og prosent er å kunne se dette som relative størrelser. En misoppfatning noen elever kan være i, er at de oppfatter brøker (eller prosenter) som konstante størrelser, for eksempel at `(1)/(2)` alltid er større enn `(1)/(3)`. Dette stemmer hvis de arbeider med tallinje og betrakter brøkene som tallstørrelser eller brøk som operator på samme mengde.
Eksempel: `(1)/(2)` av 12 drops vil alltid være mer enn `(1)/(3)` av 12 drops.
Misoppfatningen vil vise seg dersom brøkene virker på ulike mengder eller helheter, eller hvis mengden eller helheten er ukjent.
Eksempel: Astrid spiser halvparten av sine drops, og Olav spiser en tredel av sine drops. Hvem spiser flest drops? Slik eksemplet er formulert, er det umulig å svare på oppgaven, siden vi ikke vet hvor mange drops Astrid og Olav har. En del elever vil likevel svare at Astrid spiser flest drops, fordi `(1)/(2)` alltid er større enn `(1)/(3)`. Dersom Astrid hadde 12 drops og Olav 24, ville svaret vært at Olav spiser flest drops (`(1)/(2)` av 12 drops er alltid mindre enn `(1)/(3)` av 24 drops).
Alle situasjoner med prosent er varianter av del av en helhet, der helheten er det samme som 100 %. Helheten endrer seg dersom det skjer en økning (forstørring) eller en minskning (forminskning.) Noen elever har problemer med å forstå at helheten kan endre seg.
Dersom oppgaven er å finne prosenter av en mengde med utgangspunkt i to eller flere delmengder, vil en del elever addere de ulike prosentene. Eksempel: I en butikk er det 10 % avslag på klær. Noen elever vil svare at 10 % avslag på jakke og 10 % avslag på bukse til sammen blir 20 % avslag.
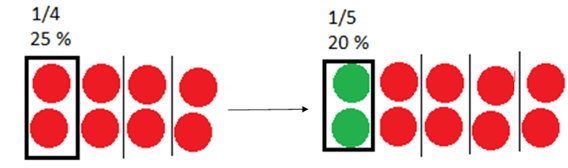
På samme måte vil noen elever tenke at prosenten eller brøkdelen er den samme når de legger til enheter i en mengde og deretter tar bort samme mengde. Eksempel: Olav har 8 brikker og legger til 25 % (`(1)/(4)`) av antallet, slik at han har 10 brikker. Etterpå tar han bort 2 brikker. En del elever vil da si at han tok bort like stor del av brikkene, 25 % eller `(1)/(4)`, mens han i realiteten tok bort 2 av 10, som utgjør 20 % (`(1)/(5)`).
Oppgaver
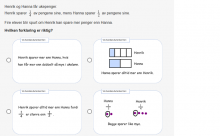
I prøven Misoppfatninger knyttet til brøk og prosent er det fire oppgaver innen denne kategorien. To av oppgavene er med i prøven for 5.–7. trinn, og alle oppgavene er med i prøven for 8.–10. trinn. Tre av oppgavene ser du nedenfor.
Analyse
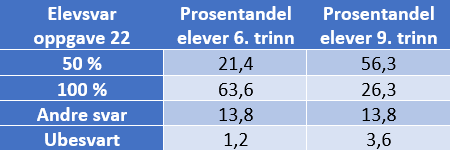
I oppgave 22 skal elevene finne ut hvor stor del av en hel fotballkamp Kjell skal spille, når han skal spille 30 % av tiden i førsteomgang og 70 % av tiden i andreomgang. Elever som ikke tar hensyn til helheten, legger sammen de to prosenttallene, 30 % og 70 %, og svarer 100 %.
Som vi ser av tabellen, gjelder dette godt over halvparten av elevene på 6. trinn, mens andelen som svarer dette på 9. trinn, er mer enn halvert sammenlignet med 6. trinn. Det kan naturlig nok skyldes at elevene på 9. trinn har et mye bedre utviklet prosentbegrep, men også at elevene på 9. trinn er flinkere til å vurdere svaret sitt, og at flere dermed unngår å svare at Kjell spiller hele fotballkampen.
Oppgave 15 tester samme misoppfatning som oppgave 22, ved at 10 % av guttene og 10 % av jentene i en klasse skal velges som trivselsledere. Det som skiller oppgavene, er at i oppgave 22 får elevene vite at fotballomgangene er like lange, men de får ikke vite noe om det er like mange jenter som gutter i klassen. I tillegg får de som legger sammen prosenttallene, 20 %, noe som trolig oppleves som et mer sannsynlig svar enn 100 % i oppgave 22. Andelen elever som svarer 20 %, er 87 % på 6. trinn og 69 % på 9. trinn, og nesten 90 % av elevene som svarer 100 % i oppgave 22, svarer 20 % i oppgave 15. Det gjelder både 6. og 9. trinn.
I oppgave 9 i prøven for 8.–10. trinn blir elevene utfordret i prosentgrunnlag, der prisen på en fotball som i utgangspunktet koster 200 kr, blir satt ned med 50 % og så 50 % på nytt. Også denne oppgaven ligner på oppgave 22, men her får elevene opplysninger nok til å kunne regne med prosent. Det er trolig en grunn til at flere løser oppgaven riktig. Resultatet av analysene viser imidlertid at 85 % av elevene som svarer at nyprisen blir 0 kr i oppgave 9, svarer 20 % i oppgave 15. Tilsvarende tall for de som svarer 100 kr, er 83 %.
Oppgave 30 i prøven for 8.–10. trinn utfordrer elevene til se på brøk som operator. De skal ta stilling til ulike forklaringer om det er mulig at `(1)/(4)` av noe kan være større enn `(1)/(2)` av noe annet. Forklaringene i alternativene er basert på en åpen utprøving. Analysene viser at 34 % av elevene velger riktig forklaring. Det er forklaringen med arealmodellen, der elevene sammenligner brøkene av samme helhet, som flest elever velger, 54 %.
Elevsvar
Nedenfor er noen elevsvar fra da oppgavene ovenfor ble testet ut på papir, uten svaralternativer. Svarene er gitt av elever fra 5. til 10. trinn.