Matematikk 1T, Eksempeloppgave med graftegner og CAS

Del 2, oppgave 5

Oppgaven er hentet fra forslag til ny eksamensordning for MAT1013 Matematikk 1T (2012, s. 10). Oppgaven må løses med CAS eller graftegner for å gi full uttelling.

Funksjonen \(f\) er gitt ved \[f(x) = 0,5x^3 - 3,25x^2+ 6x - 2,25 \ \ , x \in [-1, 4]\]

Grafen til \(f\) har tre tangenter som går gjennom origo.

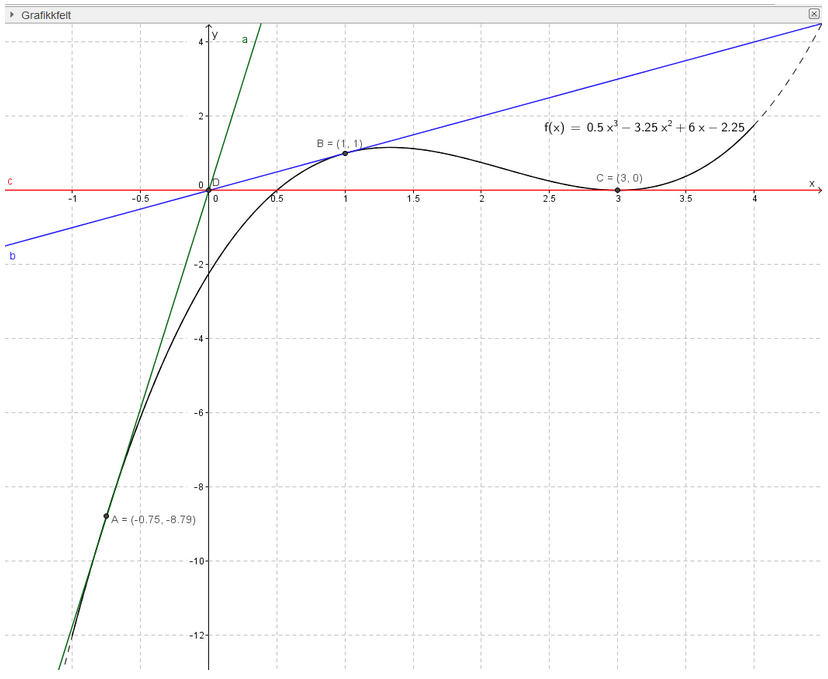
  1. Tegn grafen til \(f\) i et koordinatsystem, og skisser de tre tangentene.
  2. Skriv opp likningen for en tangent til grafen til \(f\) som går gjennom punktet \((x_1, f(x_1))\). Bruk denne likningen til å finne de tre punktene der grafen til \(f\) har en tangent som går gjennom origo.

Løsningsforslag

graftegner9.PNG

graftegner10.PNG

 

  1. Jeg tegner grafen og skisserer de tre tangentene gjennom origo.

    Grafen til \(f\) og de tre tangentene \(a\), \(b\) og \(c\) gjennom origo er vist i figuren over.
  2. En tangent til \(f\) gjennom punktet \((x_1, f(x_1))\) har ligningen \[y - f(x_1) = f'(x_1)(x - x_1)\] Ved hjelp av CAS, finner jeg ligningen i rad 2 i CAS-vinduet over. For å finne de tre tangentene gjennom origo, setter jeg \(x = 0\) og \(y = 0\) i ligningen og løser denne med hensyn på \(x_1\) (rad 4). Da får jeg \(x\)-verdiene til punktene tangentene går gjennom på grafen til \(f\). Jeg setter inn i \(f(x)\), og finner punktene:

    \(A = (-3/4, - 1125/128) \approx (-0,75, -8,79)\), \(B = (1, 1)\), \(C = (3, 0)\)

Fil

GeoGebra-fil til nedlasting

Kommentarer

Oppgaven er betegnet som CAS eller graftegner. En god løsning er å utnytte samspillet mellom de to verktøyene ved å lage en skisse med graftegner og deretter gjøre beregningene med CAS. En slik løsning vil også gjøre det lettere for elevene å avgjøre om svaret de kommer fram til er riktig.

En vanlig feil er at elevene skriver f’ for å finne det deriverte i CAS, men da skjer det ingenting. Riktig skrivemåte er f’(x).

 

GeoGebra

Didaktiske refleksjoner

a)

Elevene skriver funksjonen inn slik som den er, og avgrenser definisjonsområdet etterpå ved hjelp av kommandoen Funksjon[...].

Det finnes flere måter for å skissere tangentene:

1) Tegne linjer fra origo til grafen og flytte punktet til linjen blir en tangent.

2) Tegne tangenter på grafen og flytte berøringspunktet til tangenten går gjennom origo.

Her har vi valgt å tegne grafen for alle x-verdier som en stiplet graf, men vi kunne også valgt å skjule den helt. Den heltrukne grafen viser grafen for x = [-1, 4]. Innskriving og kommmandoer i GeoGebra blir litt enklere dersom man velger å ikke avgrense funksjonen til et bestemt definisjonsområde, og det lønner ser derfor ofte å vente til slutt med å avgrense grafen til definisjonsområdet. Flere av CAS-kommandoene virker dessuten ikke på den avgrensede funksjonen.

Det kan være utfordrende å finne de tre tangentene. Elevene bør ha øvd på å flytte punkter som ligger på grafen.

b)

Løses med CAS. Start med å skrive navnet til funksjonen i CAS.

Resultatet kan kontrolleres ved å sammenligne skissen med svaret.

Her utnytter vi samarbeid mellom vinduene i GeoGebra. Det er lurt at elevene blir vant med å skissere en fremgangsmåte før de begynner med å løse oppgaven i GeoGebra.

Forklaringene kan stå i CAS feltet, men da blir feltet langt og det er vanskelig å få utskriften på en side.