Matematikk S1. Eksempeloppgave med graftegner
Oppgaven er hentet fra forslag til ny eksamensordning for REA3026 Matematikk S1 (Utdanningsdirektoratet 2012, s. 30).
Del 2, oppgave 4
Et jernbaneselskap skal innrede et nytt togsett. Sittepalssene i toget er fordelt på første klasse og andre klasse. Selskapet ønsker å fordele setene slik at billettinntektene blir størst mulig. Etterspørselen er stor, så de regner med å selge alle billettene på hver avgang.
La \(x\) være antall seter på første klasse, og la \(y\) være antall seter på andre klasse.
Fordelingen av seter er gitt ved følgende begrensninger:
\[60 \leq y \leq 400\]
\[0 \leq x \leq 150\]
\[y \leq -\frac{1}{3}x+250\]
\[y \leq -\frac{4}{3}x+360\]
Billettprisen på første klasse er 820 kroner per sete, og prisen på andre klasse er 465 kroner per sete.
Bestem det antallet seter på første klasse, og det antallet seter på andre klasse som gir selskapet størst mulig samlet inntekt per avgang.
Bestem hvor stor denne inntekten bli.
Løsningsforslag
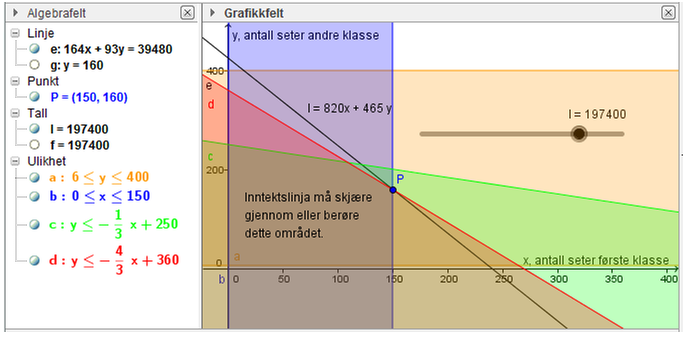
Jeg skriver ulikhetene direkte inn i GeoGebra, og bruker forskjellige farger. Figuren viser det området der alle begrensningene gjelder. Den svarte linja er inntektene til togselskapet på en avgang gitt ved ligningen \(I=820x+465y\). Ved å endre på glideren i GeoGebra, finner jeg at inntekten er størst i punktet \(P\). Der er \(x=150\), og \(y=-\frac{4}{3}\cdot 150+360= 160\). Det er vanskelig å vurdere helt nøyaktig ut fra figuren når inntektslinja går gjennom punktet \(P\). Ved regning finner jeg at den største inntekten er \(820 \cdot 150 + 465 \cdot 160 = 197400\).
Inntektene blir størst med 150 seter på første klasse og 160 seter på andre klasse. Den største inntekten blir 197 400 kr per avgang.
Kommentarer
GeoGebra er godt egnet til å få fram forståelse om lineær optimering. Når begrensningene er lagt inn som ulikheter i GeoGebra, er det ikke mulig å bruke verktøyet for skjæringspunkter til å finne hjørnene i mangekanten som avgrenser \(x\)- og \(y\)-verdiene. Hvis man ønsker å bruke verktøyet for skjæringspunkter, må man legge inn avgrensningslinjene som likninger.
|
GeoGebra |
Didaktiske refleksjoner |
|
60 <= y <= 400 |
Disse ulikhetene avgrenser området for x og y. Det er lurt å velge forskjellige farger på ulikhetene. I denne oppgaven har vi valgt å vise algebrafeltet for å få fram hvilke uttrykk som hører med til hver farge. OBS! Dersom elevene ikke har tilgang til fargeskriver på eksamen, må de markere tydelig med tekst på figuren slik at det går klart fram hvilke områder som hører med til hvilke uttrykk. |
|
I = 820 x+ 465 y Opprett glider for \(I\), og trekk i glideren slik at inntekten blir størst mulig samtidig som begrensningene for \(x\) og \(y\) er oppfylt. |
Ved å endre på glideren for \(I\), ser man direkte hvordan inntektslinja flytter seg, og man finner lett hvilket hjørne som gir størst inntekt. |
|
Finn koordinatene til det hjørnet der inntekten er størst, og regn ut denne inntekten. |
Figuren er ikke nøyaktig nok til at man kan lese av maksimal inntekt direkte av glideren. |
Åpne dette dynamiske arbeidsarket for å se hvordan oppgaven er løst i GeoGebra.