Matematikk 1P. Eksamensoppgave med graftegner
Oppgaven ble gitt som eksamensoppgave i Matematikk 1P høst 2013 (Utdanningsdirektoratet, s. 21).
Del 2, oppgave 5
Funksjonen \(f\) gitt ved \[f(x)=3x^3-48x^2+162x+300\] viser hvor mange tonn fisk \(f(x)\) det var i en fiskebestand \(x\) år etter år 2000.
- Tegn grafen til \(f\) for \(0 \leq x \leq 10\).
- Når var fiskebestanden minst?
Hvor mange tonn fisk var det i fiskebestanden da? - Bestem skjæringspunktet mellom grafen til \(f\) og linjen med likning \(y=200\).
Hva forteller koordinatene til dette punktet om fiskebestanden? - Hvor stor var den gjennomsnittlige endringen i fiskebestanden per år i perioden 1. januar 2003 - 1. januar 2007?
Vi har valgt å vise to forskjellige løsningsforslag. Etter vår vurdering bør begge forslag gi full uttelling, men alternativ II (eller en blanding av I og II) er antakelig enklere for mange elever.
Løsningsforslag I
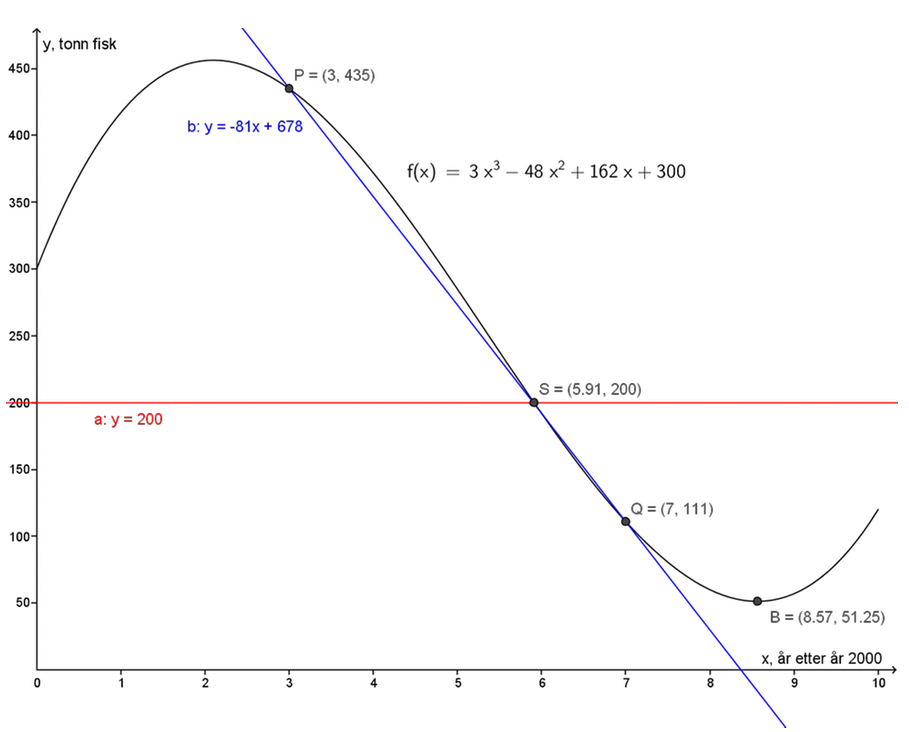
- Grafen til \(f\) er tegnet på figuren over.
- Jeg bruker kommandoen Ekstremalpunkt[f], og får både topp- og bunnpunktet til grafen. På figuren vises bunnpunktet \(B=(8.57, 51.25)\) der fiskebestanden er minst.
Fiskebestanden var minst i år 2008. Bestanden var da på 51 tonn. - Jeg skriver y=200, og finner skjæringspunktet \(S=(5.91, 200)\) med grafen `f`.
Fiskebestanden var på 200 tonn i slutten av 2005. - Jeg skriver inn P=(3,f(3)) og Q=(7,f(7)), og tegner den rette linja \(b\) gjennom disse punktene. Av ligningen til linje `b` ser jeg at stigningstallet er -81.
Det betyr at fiskebestanden i gjennomsnitt sank med 81 tonn per år fra 1. januar 2003 til 1. januar 2007.
Kommentarer I
Denne typen oppgave finnes på alle eksamener i Matematikk 1P. Erfaring viser at elever som er vant til å bruke graftegner, ofte vil lete seg fram til funksjonsoppgaven og løse den først.
Utsagn som «Jeg finner skjæringspunktet…», eller «Skjæringspunktet mellom linjene er…» kommuniserer godt. Det er unødvendig å gå i detalj om hvilken metode som er brukt, for eksempel: «Jeg finner skjæringspunktet mellom linjene med verktøyet «Skjæring mellom to objekt».
|
|
GeoGebra |
Didaktiske refleksjoner |
|
a) |
f(x)= 3x^3-48x^2+162x+300 Funksjon[f,0,10] |
Elevene starter med å skrive inn funksjonen \(f(x)\). For å avgrense grafen til intervallet \(0\leq x \leq 10\), må man i GeoGebra bruke kommandoen Funksjon[f,0,10]. |
|
b) |
Ekstremalpunkt[f] |
Elevene må kjenne til begrepet ekstremalpunkt og klare å skille mellom maksimum og minimum. Tolking av svaret krever et tekstsvar. |
|
c) |
Tolkning av graf og skjæringspunkt |
|
|
d) |
Beregne gjennomsnittlig endring ved å se på stigningstallet til linja gjennom to punkter på grafen. |
En elev som løser oppgaven på denne måten, viser høy kompetanse. |
Løsningsforslag II
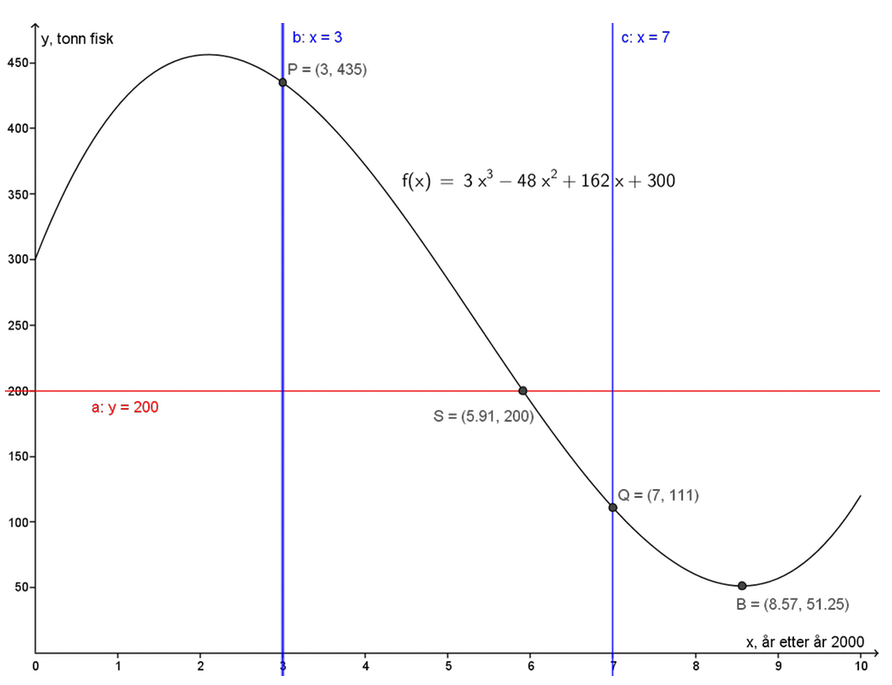
- Grafen til \(f\) er tegnet på figuren over.
- Jeg bruker kommandoen Ekstremalpunkt[f], og får både topp- og bunnpunktet til grafen. På figuren vises bunnpunktet \(B=(8.57, 51.25)\) der fiskebestanden er minst.
Fiskebestanden var minst i år 2008. Bestanden var da på 51 tonn. - Jeg skriver y=200, og finner skjæringspunktet \(S=(5.91, 200)\) med grafen \(f\).
Fiskebestanden var på 200 tonn i slutten av 2005. - Jeg skriver x=3 og finner skjæringspunktet med grafen \(f\), \(P=(3, 435)\). Så skriver jeg x=7 og finner skjæringspunktet med grafen, \(Q=(7, 111)\). Jeg finner endringen i bestanden i løpet av disse 4 år: \(111-435 = -324\). Endringen per år er \(\frac{-324}{4}= -81\).
Det betyr at fiskebestanden i gjennomsnitt sank med 81 tonn per år fra 1. januar 2003 til 1. januar 2007.
Kommentarer II
|
|
GeoGebra |
Didaktiske refleksjoner |
|
d) |
Beregne gjennomsnitt |
Mange elever vil antakelig bruke kalkulator til å beregne den gjennomsnittlige veksten.
|