Andre problemer knyttet til Tallregning
For mange elever er det å beherske regneartene ensbetydende med å kunne algoritmene. De skiller ikke mellom regnearten – hvilke ideer som er knyttet til for eksempel multiplikasjon og utregningsmåten – og algoritmen.
I multiplikasjonsoppgaver med flere faktorer kombinerer en del elever addisjon og multiplikasjon. Noen elever adderer to eller flere faktorer, slik at de sitter igjen med to tall som de multipliserer. Eksempel: 2 ∙ 2 ∙ 2 ∙ 3 = 18 fordi 2 + 2 + 2 = 6 og 6 ∙ 3 = 18. Andre elever gjennomfører multipliserer først to og to faktorer, for så å summere produktene.
Eksempel: 2 ∙ 2 ∙ 2 ∙ 3 = 10 fordi 2 ∙ 2 er 4, 2 ∙ 3 er 6, og 4 + 6 er 10.
Elever som ser på desimaltall som par av hele tall, behandler tallene deretter. Eksempel: De utfører 5 · 3,5 ved å tenke 5 · 3 og 5 · 5. De to svarene setter de sammen med komma som skilletegn, slik at svaret på multiplikasjonsstykket blir 15,25. Denne misoppfatningen er nærmere beskrevet under Misoppfatninger knyttet til tall.
Å løse multiplikasjonsoppgaver ved hjelp av gjentatt addisjon er en strategi som fungerer i mange tilfeller, men er lite effektiv i multiplikasjon med store tall. Strategien vil ikke være mulig å bruke når begge faktorene er desimaltall. Spesielt kommer det til syne når faktorene er i tallområdet 0–1.

I multiplikasjonsoppgaver der den ene faktoren er 0, tenker en del elever at det er det samme som å multiplisere med 1. Eksempel: 3 ∙ 0 = 3, fordi null er «ingenting». Elevene har erfaringer fra addisjon med at tallet forblir det samme om de legger til null. De samme elevene kan oppfatte oppgaven annerledes hvis 0 er første faktor i regnestykket. Når de begynner med 0 er det lettere å forstå at det ikke blir flere, uansett hvor mange ganger de får 0. Det stemmer også med erfaringene de har fra addisjon.
Eksempel: 0 ∙ 3 = 0 fordi 0 + 0 + 0 er 0. Disse elevene kan ha problemer med å forstå at 3 ∙ 0 = 0 ∙ 3, at kommutativitet også gjelder når 0 er en av faktorene.
Elevene kan ha nytte av å arbeide med oppgaver der de kan utnytte identitetselementene 0 og 1 i regneuttrykk, 0 ved addisjon og subtraksjon og 1 ved multiplikasjon og divisjon.
Elever som ser på det å kunne multiplikasjon som det å kunne algoritmen eller huske multiplikasjonstabellen, kan ha problemer med å se på multiplikasjon og divisjon som motsatte operasjoner (tilsvarende addisjon og subtraksjon). Eksempel: (13 ∙ 7) : 7 = 13. De vil ikke umiddelbart se at svaret blir 13, men først regne ut multiplikasjonen, og deretter dividere med 7.
Oppgaver
I prøven misoppfatninger knyttet til tallregning er det seks oppgaver i prøven for 5.–7. trinn og fem i prøven for 8.–10. trinn som tester de misoppfatningene som er beskrevet ovenfor. Fire av dem ser du nedenfor.
Analyse
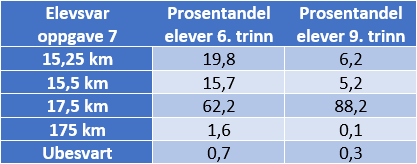
I oppgave 7 skal elevene utføre en multiplikasjon der en av faktorene er et desimaltall. Elevsvarene tyder på at mange får problemer på grunn av manglende kunnskaper om posisjonssystemet, når de skal multiplisere med desimaltall. Det mest høyfrekvente feilsvaret er 15,25 km, som kommer av at elevene ser på desimaltall som par av hele tall. De multipliserer delen foran og etter kommaet med 5, og får da 15 foran kommaet og 25 etter kommaet. Deretter settes de to delene sammen med komma som skille. Denne misoppfatningen blir testet grundig i prøven Tall.
Vi ser også at mange elever svarer 15,5 km. Som elevsvarene nedenfor viser, kommer det av at elevene multipliserer heltallsdelene av faktorene og lar desimaldelen stå.
I oppgave 4 skal elevene multiplisere flere faktorer. Elevsvarene viser at mange elever omdefinerer oppgaven i et forsøk på å redusere antall faktorer til to. På 6. trinn er det 16 % av elevene som svarer 10 (2 ∙ 2 + 2 ∙ 3) og 15 % som svarer 18 ((2 + 2 + 2) ∙ 3).
Oppgave 14 (5.–7. trinn) tester om elevene klarer å multiplisere 345 med 0. De aller fleste klarer det, men 11 % på 6. trinn svarer 345. Det tyder på at de er i en misoppfatning om at å multiplisere med 0 er det samme som å multiplisere med 1. Under piloteringen prøvde vi også en variant av oppgaven der regnestykket var 0 ∙ 345. Andelen som svarte 345, var da 6 %, altså lavere enn for varianten som er med i prøven.
Oppgave 20 tester om elevene har forstått sammenhengen mellom multiplikasjon og divisjon. Oppgaven inneholder tall som skal være vanskelige å regne med. Det er for å redusere antall riktige svar som kommer av at elevene regner ut riktig svar. Vi kan ikke utelukke at noen som svarte riktig under piloteringen gjorde det. Svært mange ulike feilsvar tyder likevel på at elevene prøver å regne ut svaret, men regner feil. Det er bare ett høyfrekvent feilsvar. Det er 279,174, tallet som står på lommeregneren på bildet. I tillegg hadde oppgaven en høy andel ubesvart ved siste pilotering. Det var 57 % av elevene på 6. trinn og 66 % av elevene på 9. trinn som løste oppgaven riktig.
Elevsvar
Nedenfor er noen elevsvar fra da oppgavene ovenfor ble testet ut på papir, uten svaralternativer. Svarene er gitt av elever fra 5. til 10. trinn.