Differensen mellom teller og nevner avgjør størrelsen til brøken
Misoppfatninger knyttet til likeverdige brøker og sammenligning av størrelser.
Noen elever tar utgangspunkt i kunnskap de har om de naturlige tallene, når de skal avgjøre størrelsen på brøker. De ser på teller og nevner som uavhengige tallstørrelser, og tar ikke hensyn til forholdet mellom dem. Derfor ser de på differansen mellom telleren og nevneren når de skal vurdere størrelsen på brøken. Jo mindre differansen er, jo større er brøken. Eksempel: Brøken`(3)/(5)` er større enn`(6)/(9)` fordi differensen mellom 3 og 5 er mindre enn mellom 6 og 9. Strategien vil alltid fungere dersom elevene sammenligner brøker med samme nevner, men den vil også fungere i andre tilfeller. Dersom elevene sammenligner `(1)/(2)` med `(2)/(5)`, vil feiltenkingen gi riktig svar.
Misoppfatningen vil også kunne påvirke forståelsen av likeverdige brøker. Eksempel: Noen elever tenker at `(3)/(4)` og `(5)/(6)` er like store, fordi differansen mellom teller og nevner er lik.
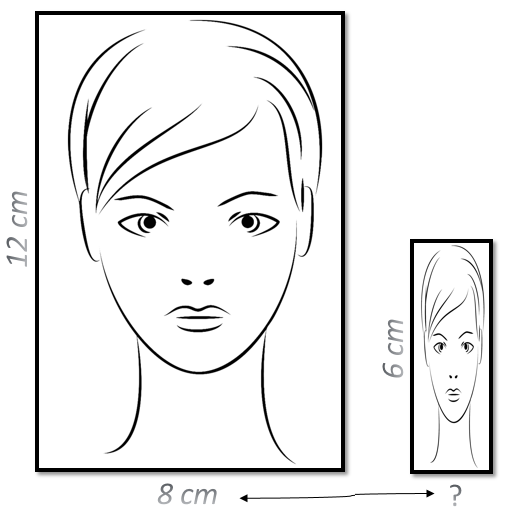
Misoppfatningen kan i tillegg komme til syne i problemer der multiplikative strukturer inngår som for eksempel brøk som forholdstall. Eksempel: Line skal forminske et bilde, slik at størrelsen på bildet blir halvert. Høyden blir halvert, `(1)/(2)` ∙ 12 cm = 6 cm. Elever som ser på dette som en additiv sammenheng, vil tenke forskjell i stedet for forhold (12 cm – 6 cm = 6 cm). Når høyden minker med 6 cm, subtraherer de samme lengde fra bredden (8 cm – 6 cm = 2 cm). Disse elevene vil mene at `(6)/(12)` er det samme som `(2)/(8)` fordi differansen mellom teller og nevner er 6 i begge brøkene. Konsekvensen av tenkingen kommer godt til syne i figuren til høyre, der proporsjonene i bildet er endret etter forminskningen.
Oppgaver
I prøven Misoppfatninger knyttet til brøk og prosent er det fire oppgaver i prøven for 5.–7. trinn og tre i prøven for 8.–10. trinn som tester denne misoppfatningen. Tre av dem ser du nedenfor.
Analyse
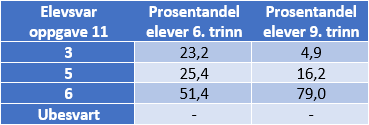
I oppgave 11 skal elevene bestemme nevneren i en brøk når `(2)/(3) = (4)/(?)` De som vurderer størrelsen på brøkene ut fra differansen mellom teller og nevner, ser at differansen er 1 i `(2)/(3)`. For at disse elevene skal få samme differanse i den andre brøken, må nevneren i den være 5. Ut fra tabellen ser vi at 25 % på 6. trinn og 16 % på 9. trinn svarer det.
I oppgave 13 i prøven for 5.–7. trinn og oppgave 21 for 8.–10. trinn skal elevene velge en brøk som er likeverdig med `(3)/(4)`. Av elevene som svarer 5 i oppgave 11, svarer 63 % at `(4)/(5)` har samme verdi som `(3)/(4)`. Det gjelder både for elever på 6. og 9. trinn.
I oppgave 8 skal elevene velge en brøk som har verdi mellom `(1)/(2)` og `(2)/(3)`, to brøker der differansen mellom teller og nevner er lik i begge. 22 % av elevene på 6. trinn og 37 % av elevene på 9. trinn løser denne oppgaven riktig, og det mest høyfrekvente feilsvaret på begge trinn er: «Det er umulig å lage en brøk med verdi mellom `(1)/(2)` og `(2)/(3)`»
Elevsvar
Nedenfor er noen elevsvar fra da oppgavene ovenfor ble testet ut på papir, uten svaralternativer. Svarene er gitt av elever fra 5. til 10. trinn.





