Teller (nevner) eller prosent er et isolert tall
Misoppfatninger knyttet til teller (nevner) og prosent som del av en helhet.
Noen elever forholder seg bare til telleren (eller nevneren) i arbeidet med brøk. De vil i noen tilfeller få riktig svar med denne tenkningen.
Eksempel 1: Elevene skal fargelegge `(1)/(3)` av tre sirkler. De som ser på telleren som et isolert tall, vil få rett svar selv om de er i en misoppfatning. Andre elever fargelegger alle tre sirklene fordi de ser på nevneren som et isolert tall.
Eksempel 2: En pizza er delt i åtte deler, og Lisa spiser `(3)/(8)` av pizzaen. Elever som ser kun på telleren, svarer tre pizzastykker og får riktig svar. Dersom oppgaven er at Lisa spiser `(1)/(4)` av pizzaen, svarer de at Lisa spiser ett pizzastykke, selv om pizzaen er delt i åtte deler.
Alle situasjoner med prosent er varianter av temaet del av en helhet. Noen elever ser også på prosenttallet som et isolert tall, og blander sammen enhet og prosenttall. Eksempel: En vare koster 200 kr, og prisen øker med 10 %. Den nye prisen blir 200 kr + 10 kr, fordi 10 % for disse elevene er det samme som 10 enheter (kroner i dette eksemplet). Samme strategi brukes når de skal finne prosenttallet. Dersom prisen på en vare øker fra 200 kr til 220 kr, vil noen elever si at økningen er 20 %.
Oppgaver
I prøven Misoppfatninger knyttet til brøk og prosent for 5.–7. trinn er det seks oppgaver som tester denne misoppfatningen, mens det er fem oppgaver i prøven for 8.–10. trinn. Tre av oppgavene ser du nedenfor.
Analyse
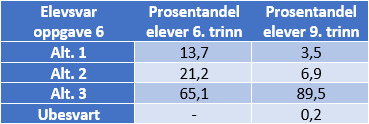
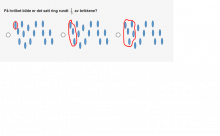
I oppgave 6 skal elevene velge figuren der det er satt ring rundt `(1)/(3)` av en mengde, i dette tilfellet 12 brikker. Elever som ser på telleren (nevneren) som et isolert tall, vil velge alternativ 1, der det satt ring rundt 1 brikke (telleren i `(1)/(3)`), eller alternativ 2, der det er satt ring rundt 3 (nevneren). Som tabellen viser, er det flest elever som velger det alternativet som viser det samme som nevneren.
Resultatene av analysen viser at elevene også er i denne misoppfatningen når de arbeider med prosent. I oppgave 26 i prøven for 5.–7. trinn, skal de regne ny pris på en vare som kostet 40 kr når prisen øker med 20 %. Elevene som betrakter prosenttallet som et isolert tall, behandler 20 % som 20 kr og svarer 60 kr. 82 % av elevene som svarer alternativ 1 (telleren) i oppgave 6, svarer 60 kr i oppgave 26. Tilsvarende tall for alternativ 2 (nevneren) er 71 %. 99 % av elevene som løste oppgave 26 riktig, løste oppgave 6 riktig.
I oppgave 24 i prøven for 8.–10. trinn, skal elevene regne ut hvor mange prosent en pris har økt når den økte fra 30 kr til 45 kr. De som har den misoppfatningen at teller (nevner) og prosent er et isolert tall, vil her svare 15 %. 62 % av elevene som svarte dette, svarte alternativ 1 i oppgave 6, og 60 % svarte alternativ 2 i samme oppgave. 98 % av elevene som løste oppgave 24 riktig, løste også oppgave 6 riktig.
Elevsvar
Nedenfor er noen elevsvar fra da oppgavene ovenfor ble testet ut på papir, uten svaralternativer. Svarene er gitt av elever fra 5. til 10. trinn.