Modul 3 - Input

Mål
Matematikk
- Utforske vinkler i regulære mangekanter
- Algoritmisk tenking
Programmering
- Input – blokken spør tar imot informasjon fra brukeren
Oversikt over nye blokker i denne modulen
| Bevegelse | Registrere koordinatene til figuren |   |
| Gå til et tilfeldig sted | 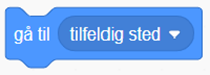 |
|
| Utseende | Bytte drakt på figuren | 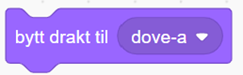 |
| Neste drakt |  |
|
| Endre farge og seks andre effekter | 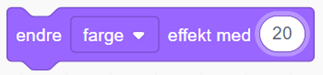 |
|
| Velge farge og seks andre effekter |  |
|
| Operatorer | Tilfeldig tall fra og med – til og med to valgte tall. | 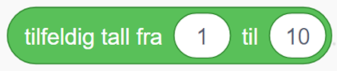 |
| Sansing | Be brukeren legge inn data |  |
| Svaret blir registrert og brukeren kan velge om svaret skal være synlig |  |
|
| Penn | Stemple avtrykk av figuren |  |
Kort oversikt
Modulen består av tre deler og bygger videre på arbeidet med kvadrater. Modulen introduserer noen få nye blokker, hvor den viktigste handler om input. Elevene får også tid til å repetere bruken av sentrale blokker, som for eksempel variabler og beregninger.
DEL 1 handler om å tegne regulære mangekanter. Del 2 utfordrer elevene på å lage mønster ved å stemple figuren. Mønstrene kan både lages ved å bruke regulære mangekanter og ved å rotere flytte og endre størrelse på figurene. Del 3 handler om vilkårlige mangekanter. Vilkårlige tre- og firkanter kan gi noen overraskende resultater. Modulen utfordrer på å kontrollere tilfeldigheten slik at man får mangekanter som tilfredsstiller visse krav.
Del 1 - Regulære mangekanter
I regulære mangekanter er alle sider like lange og alle vinkler like store. Arbeidet med regulære mangekanter tar utgangspunkt i arbeidet med kvadrater. Hvis elevene har spart det første kvadratet de laget, kan de lage kopi av det programmet og for eksempel kalle det nye programmet Regulære mangekanter. Men først en analog aktivitet.
Utforske vinkler i regulære mangekanter
Diskuter endringer
Vis elevene programmet som lager et kvadrat. Det kan du for eksempel gjøre ved å åpne programmet i Scratch. Be elevene tenke over hvilke verdier de må endre i programmet for at det skal tegne en regulær trekant. La elevene diskutere i grupper og komme med sine hypoteser. Forslagene kan gjerne skrives på tavla.
Endre verdier og utforske regulære mangekanter
Arbeidsark 03a regulære mangekanter (pdf)
Kommentarer
Spar tid på gjenbruk av kodeblokker. Elevene kan finne fram et program som tegner et kvadrat, lage kopi av det og endre navnet. Oppfordre elevene til å lage navn som sier noe om innholdet, for eksempel regulære mangekanter.
Observer elevene mens de utforsker regulære mangekanter. Mange elever vil nok støte på dette problemet: Hvorfor blir det ikke en trekant når vi snur 60 grader? La dem selv finne ut hvor mange grader de må rotere i hvert hjørne. Vent med en begrunnelse til elevene har erfaringer nok til å lete etter og kanskje finne en forklaring selv. La dem gjerne lure på begrunnelsen til dere er klare for en oppsummering i hele klassen.
Det er tilstrekkelig å endre de to verdiene i gjenta _ og snu _ for å få nye mangekanter. Men på sekskanten vi man lett se at pilen ikke ender opp i samme punkt som den startet:
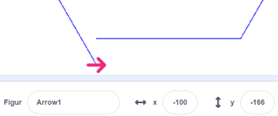
Når det blir flere kanter på figurene, må også sidelengden endres.
Oppsummering
Når elevene har laget en oversikt på antall gjentakelser og vinkler i noen mangekanter, er det tid for en felles oppsummering. En felles tabell vil være nyttig:
| Antall kanter | Vinkel (i grader) |
|---|---|
| 3 | 120 |
| 4 | 90 |
| 5 | 72 |
| 6 | 60 |
| ... | ... |
Utfordring for elevene:
Finn en sammenheng mellom vinkelen man må rotere og antall sider.
Hvorfor er det slik?
Kommentar
Eksempel på begrunnelse for en trekant.
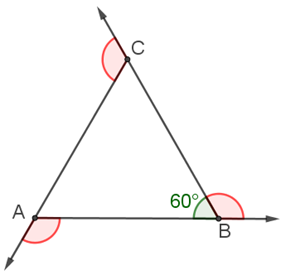
Dette skjer når trekanten blir tegnet:
- Man starter i punkt A og peker i retning B.
- I B må rotasjonen være så stor at det blir 60 grader «inne i» trekanten.
Da peker pila i retning mot C. Rotasjonsvinkelen er markert rød. - Når denne rotasjonen er utført tre ganger, peker pila i samme retning som i punkt 1.
Den samlede rotasjonen blir da 360o, og hver rotasjon er 360o : 3 = 120o.
Tilsvarende argument kan man benytte på andre regulære mangekanter.
Input fra brukeren
Når vi har sett sammenhengen mellom antall sider og vinkelen (produktet er 360) kan vi få beregnet rotasjonsvinkelen automatisk. Det kan vi gjøre ved å la elevgrupper prøve å forutsi hva dette programmet gjør og så legge opp til en diskusjon i klassen.
Tolke program
Arbeidsark 03b regulære mangekanter (pdf)
Oppsummering
La først elevene som har noe de lurer på få stille sine spørsmål. Utfordre andre elever på å svare på spørsmålene.
Kommentar
Det er strengt tatt ikke nødvendig å lage en variabel av svaret når brukeren kun gir ett input – her er det antall kanter i mangekanten. Resultatet hadde blitt det samme om variabelen «antall sider» blir utelatt.
Blokka gjenta måtte da se slik ut: 
Blokka snu _ grader måtte være slik: 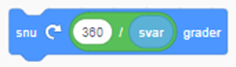
Hvis brukeren skal legge inn flere svar, må man lage en variabel av hvert svar, så det er en god vane å lage en variabel av tallene brukeren skal gi som input.
En liten detalj å merke seg: y-verdien til startpunktet er endret fra (-150) til (-140). Det er gjort for at hele spørsmålet skal vises når det blir stilt.
(-150) 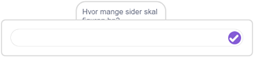
(-140) 
Lage og kjøre programmet
Når elevene lager og kjører kodeblokken med ulike antall kanter, støter de på samme utfordring som da de holdt på med arbeidsark 03a. Når antall sider blir stort nok, vil figuren bli ødelagt. Det kan selvsagt fikses ved å endre på sidelengden manuelt.
Tilpasset sidelengde og startpunkt
Det er mulig å lage program som tilpasser både startpunkt og sidelengde til antall sider i mangekanten.
Diskuter endringer
Elevene kan utfordres på å komme med forslag til hvordan programmet kan modifiseres slik at både startpunktet og sidelengden til figuren automatisk tilpasses antall sider.
Arbeidsark 03c regulære mangekanter (pdf)
Oppsummering
La elevene først komme med sine forslag til hva som må endres i programmet de har for å møte utfordringene med å lage et program som både tilpasser sidelengden og startposisjonen ut fra antall sider. Om ingen har forslag, kan man for eksempel spørre slik:
- Hvordan kan vi endre sidelengden slik at den blir mindre når antall sider øker?
- Hvilken blokk må vi gjøre noe med når vi skal endre startposisjonen?
Kommentarer
Til spørsmål 1
Det kan man gjøre ved å lage en ny variabel som kan hete «sidelengde». På figurene er variabelen laget slik:  . Ønsket var å få figurene store. Tallet er funnet med en kvalifisert gjetting og så tilpassing for å få et rundt tall å sette inn.
. Ønsket var å få figurene store. Tallet er funnet med en kvalifisert gjetting og så tilpassing for å få et rundt tall å sette inn.
Til spørsmål 2
Antall sider bestemmer også hvor pila skal stå når opptegningen begynner. Pila må plasseres slik at mangekanten får plass i resultatvinduet. y-verdien (-140) fungerer her også. Men x-verdien til startpunktet bør flyttes nærmere midten jo flere sider figuren skal ha. Når man tegner trekanten vil sidelengden bli 1000 : 3 = 333,3… Skal trekanten bli plassert midt på arket, kan man dividere sidelengden på to og la x-koordinaten for startpunktet være minus halve sidelengden. Det kan for eksempel løses ved å erstatte x-koordinaten som har vært -100 til  . Merk at blokka gå til x: _ y: _ da må flyttes slik at den ligger etter at variabelen sidelengde er beregnet.
. Merk at blokka gå til x: _ y: _ da må flyttes slik at den ligger etter at variabelen sidelengde er beregnet.
Om startpunktet lavere er enn (-140) blir mangekanten plassert mer midt på arket. Da får vi igjen problemet med at spørsmålet ikke er synlig. Det kan vi løse ved å la pilen stå i (0, 0) når spørsmålet blir stilt. Etter at antall sider er skrevet inn og sidelengden beregnet, går pila til startposisjonen.
Denne løsningen ligger som program 03-3 tilpasset sidelengde i dokumentet 03 Oversikt programmer Scratch (pdf).
En ekstra utfordring
Arbeidsark 03d mange mangekanter (pdf)
Kommentarer
Elevene kan for eksempel starte med: 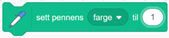 og så endre farge for hver ny mangekant:
og så endre farge for hver ny mangekant: 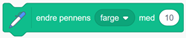
Del 2 - Lag mønster med stempel
Så langt er alle mønster og tegninger laget med pennen. Blokken stemple avtrykk, som ligger under penn-verktøyet, gir nye muligheter når man ønsker å lage mønster.
Eksempel:
En kodeblokk som lager en regulær femkant, kan modifiseres slik at man i stedet for å tegne femkanten, lager et stempel i hvert hjørne. Da må man sørge for at pennen er av. Figuren «Arrow1» er kanskje ikke den beste figuren for å lage et mønster. Figuren «Cat 2» kan være et alternativ.

La elevene leke seg med mønster
De blokkene elevene til nå er introdusert for og har en viss erfaring med å bruke, gir rike muligheter for kreativ utfoldelse, analyse av figurer og algoritmisk tenking.
Den algoritmiske tenkingen kan utvikles og styrkes ved analogt arbeid.
Kommentarer
Noen figurer kan skifte farge, for eksempel «Ball» og «Snowflake». Noen kan skifte utseende: for eksempel «Dove». Ønsker man slike effekter må man velge blokker under Utseende.
Med ballen kan man bruke blokken  som er benyttet i eksempel G. Ønsker man å endre fargen, kan man bruke blokken
som er benyttet i eksempel G. Ønsker man å endre fargen, kan man bruke blokken  .
.
Dette tilsvarer de to blokkene vi finner under penn-verktøyet:  og
og  .
.
Duen i eksempel F har to drakter, dove-a og dove-b: 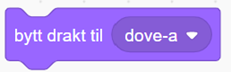 ,
,  .
.
Hver linje med duer starter med dove-a. for hver forflytning i en linje bytter figuren drakt med denne blokken: 
Del 3 - Vilkårlige mangekanter
Vilkårlige trekanter
Tolke program
La elevene arbeide i par eller grupper med arbeidsark 4a.
Arbeidsark 03f vilkårlige mangekanter (pdf)
Oppsummering
Når de fleste gruppene har fått arbeidet seg gjennom programmet linje for linje, er det tid for en felles oppsummering. La elevgruppene som har noe å spørre om, få anledning til det først. Kanskje andre elevgrupper kan svare på spørsmålene.
Deretter kan elevgrupper fortelle hva de har funnet ut.
Her er et par spørsmål du kan bruke for å utfordre elevene til slutt:
- Hvorfor må man lage de to variablene x1-verdi og y1-verdi?
- Hvorfor kan man ikke bare gjenta blokken gå til tilfeldig sted tre ganger?
Forbered utforsking
Før elevene lager og tester problemet bør man samtale om hvordan trekantene kan bli. Hvilken type trekant forekommer oftest om man for eksempel skiller mellom tre kategorier: trekanter som har bare spisse vinkler, trekanter en stump vinkel og trekanter med en rett vinkel. Når elevene skal undersøke det bør de kjøre programmet minst 30 ganger. For hver gang noterer de hvilken type trekant det ser ut til å være. Før elevene starter, bør de lage en hypotese om hvilken type trekant de vil få flest ganger.
Lag programmet og utforsk vilkårlige trekanter
La elevene lage kodeblokken og teste om programmet lager vilkårlige trekanter før de tar fatt på utforskingen. Arbeidsarket har et blankt felt for notater. La gjerne elevene diskutere ulike måter å notere på før de starter utforskingen.
Arbeidsark 03g utforsk vilkårlige trekanter (pdf)
Oppsummering
Spørsmål å undersøke etter utprøvingen:
Hvilken type trekant kom
- flest ganger
- færrest ganger
Hvorfor er det slik?
Er det mulig at resultatet ikke blir en trekant når man kjører programmet?
Hvordan kan det skje?
Kommentarer
Man kan selvsagt også notere om trekantene ser ut til å være likebeinte eller likesidede.
Eksempler på trekanter laget med programmet:
Med et raskt blikk kan man registrere A som rettvinklet, B som spissvinklet, C og D som stumpvinklet.
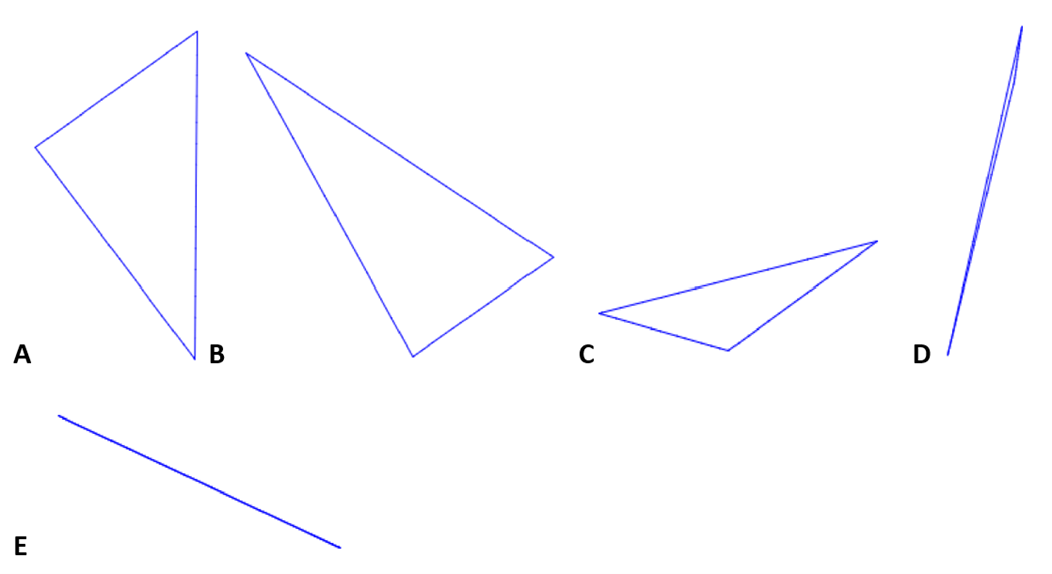
Men hva med E? Er det en trekant? Det ser ikke slik ut, og det kommer av at de tre punktene ligger på linje. Et slikt eksempel kan brukes til å utfordre elevene til å sette ord på hva som skal til for at tre tilfeldige punkter blir hjørnene i en trekant.
Vilkårlige firkanter
Kopier og modifiser
Programmet som lager vilkårlige trekanter, kan med et lite tillegg bli til et program som lager vilkårlige firkanter. Elevene kan kopiere trekantprogrammet og legge til en blokk:  .
.
Elevene kan gjerne bli utfordret på å finne ut av hva de må gjøre med programmet før de kopierer trekantprogrammet og modifiserer.
Utforsk vilkårlige firkanter
Arbeidsark 3h utforsk vilkårlige firkanter (pdf)
Kommentarer
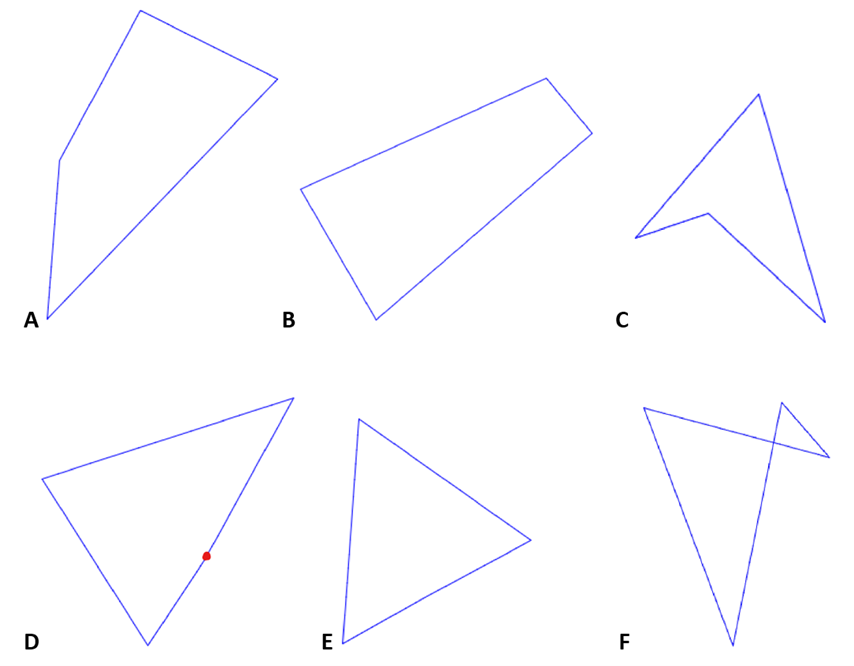
Eksemplene A-F viser «firkanter» laget med programmet som tegner vilkårlige firkanter. Med et raskt blikk kan man registrere A og B som konkave firkanter og C som en konveks firkant. D og E «ser ut som» trekanter. D har et hjørne som er markert med en rød prikk. Vinkelen er svært nær 180 grader. F er ikke en firkant, men et eksempel på en firehjørnet figur.
Om man bruker figuren Ball til å lage firkantene kan man få markert hjørnene som punkter ved å bruke blokken stemple avtrykk i hvert hjørne.
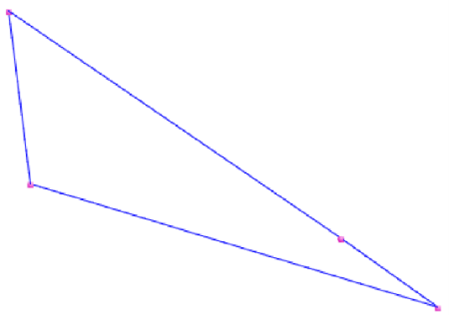
Denne mangekanten kan ved første øyekast se ut som en trekant. Siden hjørnene er markert ved å stemple avtrykk, ser vi at det er et hjørne på den ene siden. Dette hjørnet har en vinkel som er nesten 180 grader. Dersom vinkelen er nøyaktig 180 grader, så er dette en trekant.
Utfordring: Hold kontroll på mangekantene
Dette er en utfordring for elever som trenger litt ekstra å bryne seg på.
Lag program som garantert tegner
- en konkav firkant med tilfeldige lengder på sidene.
- en konveks firkant med tilfeldige lengder på sidene.
- en vilkårlig femkant
Kommentar
Et program som garantert tegner en konkav firkant, kan lages på flere måter.
I dokumentet 03 Oversikt programmet i Scratch er to ulike måter vist. Se filene 03-10 konkav firkant og 03-11 konveks firkant. Litt generelt om disse to måtene kan gis som hint til elever som tar utfordringen.
Den ene måten er å velge tilfeldige hjørner med blokka gå til x: _ y: _. Da må man styre tilfeldigheten på x-koordinatene og y-koordinatene slik at firkanten tilfredsstiller kravene til henholdsvis konkave og konvekse firkanter.
Den andre måten er å gå til et tilfeldig sted, velge en tilfeldig retning og gå en tilfeldig avstand. Også her må tilfeldighetene styres slik at kravene blir tilfredsstilt.
Begge metodene krever at man tar i bruk blokken  .
.
Hvor tilfeldig er tilfeldig?
Programmet 03-12 Hvor tilfeldig er det bruker figuren ball som er satt til 25 % størrelse. Ballen går til et tilfeldig sted og stempler et avtrykk. Blir prikkene spredt ut over hele scenen?