Modul 4 - Geometriske utfordringer

Mål
Matematikk
- Beregne omkrets og areal av vilkårlige tre- og firkanter
- Lage diagonaler i mangekanter
- Lage mønster med linjestykker
Programmering
- Benytte kjente blokker i nye situasjoner
- Vurdere om program bør deles i flere kodeblokker
Oversikt over nye blokker i denne modulen
| Operatorer | Runde av till helt tall |  |
| Finne kvadratroten til et tall | 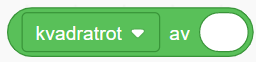 |
Kort beskrivelse
DEL 1 forutsetter at elevene er kjent med Pytagoras’ setning. Setningen blir brukt til å beregne avstander mellom tilfeldig valgte punkter. Elevene blir utfordret på å finne sammenhengen mellom diagonalen og sidelengden i kvadrater. DEL 2 utfordrer elevene på å lage linjemønster i kvadrater og stjerner med et valgt antall tagger. Del 3 dreier seg om å beregne omkrets og areal av vilkårlige tre- og firkanter. Modulen avsluttes med å utfordre elevene til å lage et spill der brukeren skal finne noe som er gjemt et sted i koordinatsystemet.
Del 1 - Beregne avstander
Hvor stor er avstanden?
Avstand mellom punkter i et koordinatsystem
Arbeidsark 04a har som mål å gjøre elevene oppmerksom at det er mulig å beregne avstanden mellom to punkter i et koordinatsystem ved å benytte Pytagoras’ setning.
Elevene får først prøve seg på avstanden mellom punktene A og B som ligger i 1. kvadrant der alle koordinatene er positive. Deretter blir de utfordret på å finne avstanden mellom punktene C og D der D har en positiv x-koordinat, mens de tre andre koordinatene er negative
Arbeidsark 04a beregne avstand (pdf)
Kommentarer
Man kan bruke mange strategier for å finne avstanden til de «usynlige» katetene. Når elevene blir utfordret på å lage en formel som beregner avstanden mellom to tilfeldige punkter med koordinatene (x1, y1) og (x2, y2), tvinges man til å tenke mer generelt. Det er nyttig når man skal lage program der det er behov for å beregne avstanden mellom to tilfeldig valgte punkter, for eksempel i spill eller arealberegninger som kommer i DEL 3.
Lengden til katetene kan skrives som (x1 – x2) og (y1 – y2). I eksemplet med punktene A og B får vi disse beregningene:
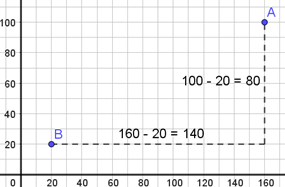
I eksemplet med punktene C (¬–180, –50) og D (50, –130) blir da katetene (–180) – 50 = (–130) og (–60) – (–130) = 70. Vi får en katet med «negativ lengde». Det er ikke noe problem siden katetene skal kvadreres og summeres før man finner avstanden mellom punktene (hypotenusen) ved å ta kvadratroten av summen.
Formelen kan for eksempel uttrykkes slik:
- avstanden = kvadratroten av ((x1 – x2)2 + (y1 – y2)2)
Denne formelen er generell og gjelder for alle avstander.
Hvis elevene har vanskelig for å komme i gang med å beregne avstandene AB og CD, kan man utfordre dem ved å spørre om det er mulig å tegne en rettvinklet trekant der de to punktene er hjørner.
Oppsummering
La elevene få presentere sine strategier for å beregne avstandene. Undersøk om noen har benyttet strategien x1 – x2 og y1 – y2 på lengden AB: 150 – 20 = 130 og 100 – 20 = 80 og la dem vente til slutt med sin presentasjon. Utfordre dem på om denne strategien også kan fungere på avstanden CD.
Fra beskrivelse til program
Når elevene har fått arbeidet grundig med matematikken som trengs for å beregne avstanden mellom to tilfeldige punkter, er det tid for å lage et program som utfører beregningen. Første steg i programmeringsprosessen bør være å lage en kort beskrivelse av hva programmet skal gjøre. Det bør elevene jevnlig utfordres på når programmet de skal lage kun bruker kjente blokker som i denne oppgaven.
Overgangen fra beskrivelse (pseudokode) til program er sjelden triviell. Et spørsmål som raskt dukker opp, kan være: Hvilke blokker kan jeg bruke til denne delen av beskrivelsen?
Bruk av variabler står ofte sentralt, så det blir også raskt spørsmål om hvilke variabler man har behov for. Arbeidsark 4i gir støtte til å finne svar på disse spørsmålene.
Hvilke blokker er aktuelle
Arbeidsark 04b fra beskrivelse til program (pdf)
Kommentarer
Forslaget i første linje er lagt inn for at elevene skal se hvordan bruk av blokker kan beskrives. Programmet kan lages med et utvalg av blokkene i oversikten. Merk at det ikke er noen linje for oppstart som til vanlig vil bestå av blokkene flagg, slett alt og penn av. Elevene får selv finne ut at det vil være nyttig. Oppgaven egner seg for samarbeid i par eller små grupper.
Oppsummering
La gjerne elevene dele forslagene sine med hverandre og oppmuntre dem til å argumentere for valgene. Det kan gi noen elever ideer til å endre eller føye til noe på eget notat. Det kan kanskje bli nødvendig å spørre elevene om det er noe de synes mangler i beskrivelsen.
Lag og test programmet
Nå skal overgangen fra beskrivelse til programkode testes ut. La helst elevene prøve seg fram uten å gi for mange hint. Elever som har store utfordringer, kan få litt hjelp gjennom arbeidsark 4c feilsøking.
Feilsøking
Finn feilen
Feilsøking får man ofte behov for når man lager dataprogram. Det er sjelden man får programmet rett på første forsøk. Her blir elevene presentert for et program som inneholder en feil.
Arbeidsark 04c feilsøking (pdf)
Kommentarer
Programmet inneholder en feil i beregning av avstand. Lengden av katetene (x-2 – x-1) og (y-1 – y-2) blir ikke kvadrert. Siden Scratch ikke har noen funksjon for å opphøye en variabel i andre må vi velge en mer tungvint løsning:

Beregningene av avstand inneholder mange desimaler. Om man er fornøyd med å få svaret avrundet til helt tall, kan man legge til ei ekstra blokk i programmet:
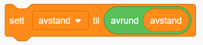
Ønsker man en desimal kan det ordnes slik:

Se program 04-2 beregne avstand i filen 04 Oversikt programmer
Lage og teste programmet
Når feilene er funnet og oppbyggingen av programmet er grundig diskutert, kan elevene lage og teste programmet.
Diagonal i kvadrat
Dette opplegget har som mål å la elevene utforske sammenhengen mellom diagonalen og sidelengden i et kvadrat. Først lager elevene et program som tegner et kvadrat med en diagonal.
Lage og gjøre forbedringer i et program
Arbeidsark 04d kvadrat med diagonal (pdf)
Kommentar
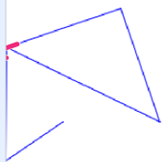
Hvis figuren går utenfor resultatvinduet, blir den ødelagt. Etter mange tester har det alltid kommet et ødelagt kvadrat før programmet er kjørt ti ganger. Man kan begrense tilfeldigheten ved å endre verdier i en eller flere av blokkene tilfeldig tall fra _ til_
Sammenheng mellom diagonal og sidelengde
Lengden til diagonalen
Utfordre elevene på å foreslå endringer i programmet som tegner et vilkårlig kvadrat med diagonal slik at programmet også beregner lengden til diagonalen.
Kommentarer
Programmet som tegner diagonal i kvadrat har en variabel for sidelengde. Det programmet kan elevene kopiere og så modifisere slik at lengden til diagonalen kan bli beregnet. Diagonalen går fra hjørnet tegningen starter i og til motstående hjørne som har koordinatene (x1, y1). For å beregne lengden til diagonalen må vi også ha koordinatene til hjørnet tegningen starter i. Det kan enkelt gjøres ved å opprette to nye variabler som tar vare på koordinatene til punktet tegningen starter i: x2 og y2. Disse to variablene kan registreres straks etter at startpunktet er valgt.
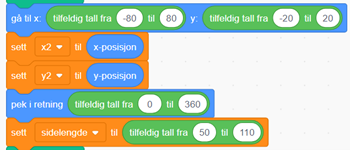
Begrensningen på disse tilfeldige verdiene garanterer at kvadratet ikke blir ødelagt.
Kodeblokk som beregner avstand, kan hentes fra programmet som allerede er laget. Ryggsekken egner seg til det. Videoen viser hvordan man bruke ryggsekken.
Se programmet 04-4 beregne avstand i dokumentet 04 Oversikt programmer (pdf).
Lage program og utforsk sammenheng
Utfordre elevene på å lage et program som
- tegner et kvadrat med diagonal og vilkårlig størrelse, orientering og plassering
- viser sidelengden og lengden til diagonalen
Kjør programmet en del ganger. Noter for hver gang sidelengden og lengden til diagonalen.
Er det noen sammenheng mellom sidelengde og diagonal?
Noen ekstra utfordringer
Diagonaler i mangekanter
La elevene prøve seg på å lage programmer som tegner
- et rektangel med diagonaler
- et parallellogram med diagonaler
- en rombe med diagonaler
- en vilkårlig firkant med diagonaler
Elevene kan også bli utfordret på å beregne lengden til
- diagonaler med ulik lengde i en tilfeldig femkant
- diagonal(er) i en annen regulær mangekant
Del 2 - Linjemønster
Hvilke blokker kjenner du til?
Det kan være tid for å stoppe opp litt og tenke gjennom de blokkene som er benyttet til nå. Det er for eksempel nyttig å reflektere rundt likheter og forskjeller mellom blokker som har noenlunde lik funksjon og hvordan man kan sette sammen blokker.
Elevene kan få arbeidsark 4e som gir en oversikt på de blokkene som til nå er introdusert. Til hver blokk eller grupper av blokker vil det være nyttig å skrive et kort notat om hva blokken gjør. Kun den første delen av arbeidsarket vises her.
Repeter
Arbeidsark 04e oversikt blokker (pdf)
Kommentar
Her vises bare kjente blokker knyttet til bevegelse. Selve arbeidsarket inneholder alle blokkene som er introdusert hittil. Det vil være nyttig for elevene om de blir utfordret på å skrive noe til enkelte blokker eller grupper av blokker. Andre blokker er det nok tilstrekkelig å kunne si noe om. Hensikten er å gjøre elevene bevisste funksjonen de enkelte blokkene har før de starter på utfordringene som kommer.
Linjer i kvadrat
Tolke program
Arbeidsark 04f linjer i kvadrat (pdf)
Kommentarer
Merk at dette programmet bruker blokken send melding. I oppgavene med kvadrater i modul 2 måtte vi bruke blokken send melding og vent. I programmet med kvadratene ble meldingen om å tegne kvadrat sendt mange ganger, så programmet måtte vente til et kvadrat ble tegnet før man kunne begynne på det neste. Her sendes meldingen kun en gang, og programmet er ferdig når alle 16 linjene er tegnet.
Oppgave b) og c) er knyttet til I-en i PRIMM-metodikken: Investigation. Denne oppgavetypen kalles sporing og er viktig for å utvikle forståelse for hvordan variabler kan brukes i programmering. Sporing består i å følge endringen til en eller flere variabler når programmet blir kjørt, beskrive hva som skjer med variabelen og når endringen skjer.
Sporing av x1 kan for eksempel forklares slik: x1-verdien settes først til (–160). Første gang blokkene i løkka gjenta 16 ganger blir kjørt er x1 (–160). Straks etterpå blir x1-verdien endret med 20 og x1 er da (–140). Andre gang løkka blir kjørt er x1 fortsatt (–140), men blir straks endret med 20 og er da (–120). Etter 16 repetisjoner vil x1 være 160. Tilsvarende beskrivelse for y2-verdien.
Hver linje har et startpunkt og et sluttpunkt. Startpunktet (x1, –160) har variabel x-verdi og fast y-verdi. Sluttpunktet (160, y2) har fast x-verdi og variabel y-verdi.
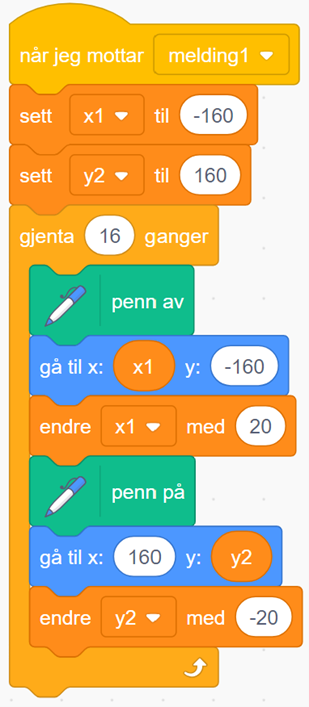 Gjenta-blokka inneholder to punkter, et startpunkt og et sluttpunkt for linjene som blir tegnet. Programmet tegner ei linje fra startpunktet som har fast y-verdi lik (-160) og ligger på den vannrette siden nede på kvadratet. Etter hver gjentakelse flyttes startpunktet mot høyre.
Gjenta-blokka inneholder to punkter, et startpunkt og et sluttpunkt for linjene som blir tegnet. Programmet tegner ei linje fra startpunktet som har fast y-verdi lik (-160) og ligger på den vannrette siden nede på kvadratet. Etter hver gjentakelse flyttes startpunktet mot høyre.
Sluttpunktet for linjene har ligger på høyre side i kvadratet fordi det har fast x-verdi lik 160. Her vil y-verdien minke med 20 for hver gjentakelse.
- Første linje blir tegnet fra startpunkt (-160; -160) til sluttpunkt (160; 160)
- Andre linje blir fra startpunkt (-140; -160) til sluttpunkt (160; 140)
- Tredje linje blir tegnet fra fra startpunkt (-120; -160) til sluttpunkt (160; 120)
- osv
Mønsteret blir slik:
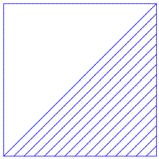
Oppsummering
Man kan for eksempel minne elevene på at da de laget mønster med kvadrater, brukte de blokken send melding og vent mens dette programmet bruker send melding. Hva er forskjellen på disse to blokkene?
Det lønner seg nok å bruke litt tid på sporingen. Elever som synes sporing er vanskelig, kan gjerne først få forklare hva som gjør det vanskelig. Hvis noen elever har en god forklaring på hva som skjer med x1 og y2, kan de bli utfordret på å forklare hva de har funnet ut for resten av klassen. Om ingen føler seg trygge kan læreren selv lede oppmerksomheten ved å stille spørsmål som for eksempel:
- Hvor i programmet møter vi x1 første gang?
- Hva er det neste som skjer med x1?
Lage og teste programmet
Når elevene har oversikt på hvordan programmet fungerer, er det tid for å lage og teste programmet.
Lag linjemønster
Tolke beskrivelse
Arbeidsark 04g er på tre sider. Figurene C, D og F fra arbeidsark 04h blir beskrevet med pseudokode.
Arbeidsark 04g pseudokode (pdf)
Utfordring
Arbeidsark 04h inneholder ideer til stjernefigurer og mønster med linjer i kvadrater. Elever som vil lage sitt eget mønster kan bruke arbeidsark 04x til planlegging.
Arbeidsark 04h ideer til mønster (pdf)
Kommentarer
En del av disse figurene passer best for de elevene som liker en ekstra utfordring. Men de fire første figurene med linjer i kvadrat skal være overkommelige med erfaringene de har med seg fra arbeidsark 4f linjer i kvadrat og arbeidsark 4g pseudokode. Elevene bør også oppfordres til å lage egne mønster. Egne mønster bør også planlegges med både tegning og beskrivelse. Bruk gjerne arbeidsark 04x rutenett 20x20 i planleggingen.
Del 3 - Beregne omkrets og areal
Arbeidsark 04i inneholder forslag til utfordringer elevene kan få. Programmeringsarbeidet er overkommelig hvis man utnytter mulighetene som ligger i gjenbruk av blokker eller hele program. Her kan det både være aktuelt med kopi av hele program og gjenbruk av kodeblokker ved å bruke ryggsekken.
Tegning og beregning
Eksempel
Når man skal lage et program som beregner omkretsen til en vilkårlig trekant:
- Lag kopi av programmet som ble laget i modul 3: 03-8 vilkårlig trekant. Modifiser programmet slik at det tar vare på koordinatene til alle tre hjørnene.
- Bruk ryggsekken og flytte kodeblokken som beregner avstand i programmet 04-1 beregne avstand inn i det nye programmet. Gjør nødvendige endringer i blokken.
Arbeidsark 04i beregne omkrets og areal (pdf)
Utfordring: Lag et spill
Et spill kan med fordel benytte en annen bakgrunn enn den hvite. Video som viser hvordan vi kan bytte bakgrunn og gjøre endringer på den endre bakgrunn.
Eksempler
Stjerner med romber
Slik kan man også lage stjerner.
Finn frosken på færrest mulig forsøk
Programmet er bygd opp av fire kodeblokker som arbeider sammen. Programmet går helt til det blir avslørt hvor frosken er.