Modul 7 - Modulo

Mål
Matematikk
- Delbarhet
- Rest ved divisjon
Programmering
- Modulo
| Operatorer | modulo |  |
| avrund ned |
avrund ned er en av svært mange valgmuligheter i denne blokka: |
|
| Lister | lengden av (velg liste) |  |
Beskrivelse av opplegget
Kort oversikt
Modulen er todelt.
DEL 1 introduserer blokka modulo. Elevene skal lære hvordan vi kan bruke blokka _mod_ til å undersøke om en divisjon «går opp» eller om det blir en rest. Elevene blir utfordret til å utforske begrepet rest ved heltallsdivisjon.
DEL 2 handler om å undersøke hvilke tall et fritt valgt tall er delelig med.
DEL 1 - MODULO
Delbar?
Fakler

Familien Jensen skulle ha selskap og sendte sønnen for å kjøpe fakler til å lyse opp ute på terrassen. Sønnen fikk med 200 kroner og han skulle kjøpe så mange fakler som mulig. Han kom tilbake med seks fakler og fikk beholde vekslepengene, 20 kroner. Hvor mye kostet hver fakkel?
Rest
Læreren ber elevene foreslå to hele tall.
Deretter dividerer læreren det første tallet på det andre tallet, og finner resten.
Resultatene kan for eksempel presenteres slik på tavla:
- 12 og 5 → 2
- 5 og 12 → 5
- 29 og 13 → 3
- 15 og 5 → 0
Listen bør inneholde eksempler både på divisjoner som gir og som ikke gir rest. Det bør også være eksempler der dividenden er mindre enn divisor som i 5 og 12.
Når det er tilstrekkelig med eksempler kan elevene utfordres på å finne tallet som skal stå etter pilen, og forklare hva de ulike tallene står for.
Eksempel på svar: Det første tallet blir dividert med det andre tallet. Tallet etter pila viser hvor stor rest divisjonen gir.
MERK: Hvis resten til divisjonen a : b er 0, betyr det at a er delelig med b, som i eksemplet med 15 og 5. Begrepet delelig med (eller delbart med) brukes om divisjoner med heltall som ikke gir rest. Divisjonen «går opp».
Hvis elevene er glade i å foreslå «stygge tall», kan det være lurt for læreren å bruke et regneark til å finne resten. Det kan enkelt lages slik:
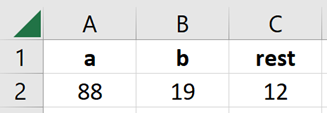

Hvis elevene bare velger store tall, kan de oppfordres til å velge tall under en viss størrelse, for eksempel 50. Da er det lettere å oppdage sammenhengen mellom de tre tallene.
Modulo
Tolke, lage og utforske
Arbeidsark 07a Blir det rest (pdf)
Kommentarer
Divisjon av to tilfeldige heltall vil i de fleste tilfeller ikke «gå opp». Det blir en rest. Det matematiske begrepet for rest er modulo. Som regel brukes kortformen mod. Modulo-regning hører til tallteorien. Tall som gir samme rest når de divideres med samme divisor er kongruente.
Oppgave a)
Hensikten med oppgaven er å utfordre elevene på å resonnere. Selv om begrepet modulo er ukjent for elevene er det mulig å tenke seg til hva a modulo b betyr. Ut fra navnet på variabelen rest kan vi tenke at det har noe med resten i en divisjon å gjøre, og at operasjonen består i å finne resten når heltallsdivisjonen a : b ikke «går opp». I den analoge aktiviteten Rest ble tallene presentert slik: 12 og 5 → 2. I matematisk fagspråk: 12 modulo 5 er 2 som altså betyr at om vi utfører divisjonen 12 : 5 blir resten 2.
Oppgave c)
Elevene skal finne hvor mange ulike verdier resten kan få når man dividerer med 7. Så lenge dividenden er 7 eller større blir resten ett av tallene 0-6. Er dividenden mindre enn 7, blir resten også 7. Generelt vil divisjon med n gi rest n når dividenden er mindre enn n. Når dividenden er n eller større vil resten være et av tallene fra og med 0 til og med (n -1).
Oppgave d)
Hvis dividenden er større enn divisor gir divisjonen 99 : 50 største rest, 49. Lar vi divisor være større enn dividenden, får vi størst rest med divisjonen 98 : 99, som gir rest 98.
Oppgave e)
Oppgaven går ut på å finne alle tall under 50 som gir rest 8 nå de blir dividert med 9. Elevene kan prøve seg fram med programmet. En strategi kan være å begynne med divisjonen 49 : 9 og så velge dividendene 48, 47, 46 osv. Det vil gi denne rekken med restverdier: 4, 3, 2, 1, 0, 8, 7, 6, 5, osv. Elevene vil da forhåpentlig oppdage at det ikke er nødvendig å prøve alle tallene. Følgende tall gir rest 8 ved divisjon med 9: 44, 35, 26, og 17. Disse tallene er kongruente fordi de gir samme rest når de blir dividert med 9. Vi sier da for eksempel at 44 er kongruent med 35 (mod 9). Kongruente tall brukes i kryptering.
Programmet kan også brukes til å undersøke delbarhet med større tall. Utfordringen for elevene blir å utnytte resten de får til å finne en dividend som gir rest 0.
Eksempel
7320 : 23 gir 6 i rest. Da må tallet som er 6 mindre enn 7320 gi 0 i rest. 7314 er delelig med 23.
Løs oppgaver
Her er noen forslag til utfordringer elevene kan løse ved å bruke programmet. Utfordringene er fine som utgangspunkt for samtaler om strategiene elevene bruker i oppgavene.
Arbeidsark 07b Oppgaver til Blir det rest (pdf)
Kommentarer
Oppgave c)
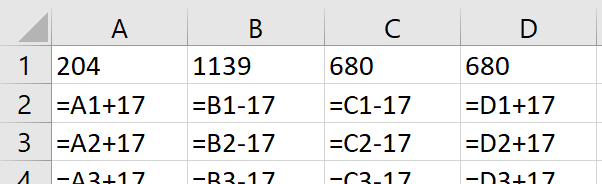
Her har du anledning til å la elevene arbeide med flere digitale verktøy. Noen elevpar vil kanskje begynne å teste tilfeldige tall mellom 200 og 1150. La dem holde på til de finner ett tall og observer om de fortsetter å undersøke tilfeldige tall, eller om de tar utgangspunkt i tallet de fant, og så legger til og trekker fra 17 for å finne de andre tallene. Da er tiden inne til å utfordre dem ved for eksempel å spørre om de kan bruke det tallet de fant til å finne nye tall. Andre strategier kan være å finne det største eller minste tallet mellom 200 og 1150 som gir rest 0 og så legge til, eller trekke fra, 17.
Det blir 56 tall i alt. Kanskje det ikke er noe poeng i å finne alle tallene, men heller snakke om strategier som gjør det mulig å finne alle tallene på en systematisk måte.
Velger dere gå for å finne alle tallene kan det være lurt å bruke et regneark til å finne dem. Dette regnearket viser de tre strategiene:
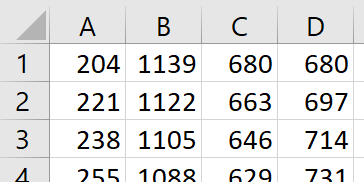
Modifisere programmet
Utfordre og diskutere
Utfordre elevene til å utvide kodeblokka slik at programmet ikke bare finner resten, men også heltallet til kvotienten. Programmet kan da gi tilbakemelding slik:
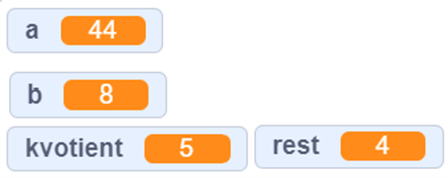
La elevene diskutere hva de må gjøre med programmet hvis det skal gi tilbakemelding både på kvotienten og resten.
Kommentarer
Det er opplagt at det er behov for ny variabel, kvotient. Men det er også behov for ei blokk som gir oss kvotienten avrundet nedover. I eksemplet ser vi at åtte går fem ganger i 44, og det er da 4 i rest. Hvis vi bare utførte divisjonen 34 : 8 ville svaret blitt 5,5. Hadde vi brukt operatoren  ville svaret sett slik ut
ville svaret sett slik ut
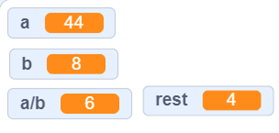
Operatoren avrund_ bruker vanlige avrundingsregler: 5,5 blir rundet av til 6. Vi må altså velge operatoren som gir mulighet for å avrunde nedover siden vi kun skal ha heltallsdelen av kvotienten. avrund ned_ er ett av mange valg på denne blokka: 
Lag programmet
Arbeidsark 07c Divisjon helt tall og rest (pdf)
Kommentarer
Oppgave b)
Oppgaven gir muligheter for å finne en a og en b uten å famle helt i blinde. Siden resten skal være mellom 10 og 15 må resten bli 11, 12, 13 eller 14. Setter vi b til 15 må a være større enn 11 ∙ 15 = 165. Da er det bare å legge til en av de fire aktuelle restene for å finne a. Men slik oppgaven er utformet fins det mange andre løsninger.
Programmet løser problem
Arbeidsark 07d Oppgaver til Divisjon helt tall og rest (pdf)
Kommentar
Dette er et eksempel på at ett og samme program kan brukes på oppgaver med to vidt forskjellige kontekster, men den matematiske problemstillingen er nøyaktig den samme. Utfordringen for elevene blir å tolke hva kvotienten og resten står for i de ulike kontekstene.
DEL 2 - BETINGELSE
Blir det rest?
Gruppestørrelse
Elever blir ofte delt i par eller grupper med 3-6 deltakere. La elevene undersøke hvordan deres klasse kan deles i nøyaktig like store grupper. Hvor mange grupper blir det av hver størrelse? Hvis antall elever er et primtall, kan læreren også være med i antallet.
Hvilket antall elever under 30 gir flest muligheter for gruppedeling med like store grupper?
Studer flytskjema
Med relativt små tall går det raskt å se hvilke tall som er delelig med et annet – i alle fall om vi kan multiplikasjonstabellene godt. Det er også til god hjelp om vi kjenner noen av metodene for å undersøke delbarhet, for eksempel at alle tall med 0 eller 5 på enerplassen er delelig med 5. Men skal vi finne alle tallene et stort tilfeldig valgt tall er delelig med, vil et dataprogram være nyttig.
Arbeidsark 07e Flytskjema til Mitt tall er delelig med (pdf)
Kommentarer
Slik flytdiagrammet er satt opp vil a hele tiden ha verdi 2. Rektanglet som viser hva som skal gjentas «Sett variabel «a» = 2»:
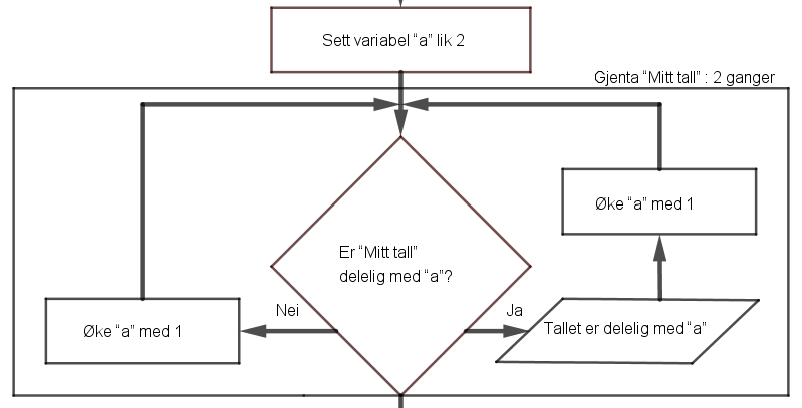
Etter at flytdiagrammet er korrigert og man har hatt en samtale om spørsmålene d) og e), kan elevene bli utfordret på å lage programmet. Elever som sliter med å få programmet sitt til å fungere, kan få arbeidsark 07f som hjelp. Elever som klarer å lage et program som fungerer kan sammenlikne sitt eget program med programmet i arbeidsark 7f, og så arbeide med oppgavene b-e.
Lage program og utforske
Arbeidsark 07f Programkode til Mitt tall er delelig med (pdf)
Kommentarer
Oppgave c og d
Oppgaven gir gode muligheter til å snakke om strategier som kan redusere antall forsøk. Hvilke tall er det IKKE nødvendig å teste?
Oppgave e
Det skjer ingen ting! 47 er et primtall, og siden programmet ikke sjekker divisjon med verken 1 eller 47 blir det ingen tilbakemelding.
Spar faktorene i ei liste
Programmet Mitt tall er delelig med kan endres slik at alle tallene variabelen «Mitt tall» er delelig med, blir samlet i ei liste. Vi får da listet opp alle faktorene i tallet vi undersøker. I programmet har vi valgt å ikke ta med 1 og tallet selv som faktorer, siden det gjelder alle tall. Det er heller ikke vanlig å ta med 1 og tallet selv når vi faktoriserer tall.
Elevene bør først utfordres på å sammenlikne flytskjemaet for programmet de allerede har laget, med flytskjema for det programmet de nå skal lage.
Arbeidsark 07g Flytskjema til Mitt tall er delelig med - liste (pdf)
Kommentarer
Hvis elevene sammenlikner med flytskjemaet i 07e som inneholder en feil, vil det være to forskjeller:
- Rektanglet som viser hva som skal gjentas «Mitt tall : 2 ganger»
- Parallellogrammet med teksten «Tallet er delelig med» er erstattet med et rektangel med teksten «Spar «a» i ei liste»
Elevene kan selvsagt utfordres på å lage programmet Mitt tall er delelig med – liste uten noen ekstra hjelp. Elever som trenger noe ekstra hjelp kan få det gjennom arbeidsark 07h.
Lage og teste program
Arbeidsark 07h Sammenlikne programmer (pdf)
Kommentarer
Oppgave a
Blokka  er fjernet.
er fjernet.
Blokka  er lagt til i slutten av programmet. Det er strengt tatt ikke nødvendig å bruke denne blokka. Nederst på listen står det hvor lang den er:
er lagt til i slutten av programmet. Det er strengt tatt ikke nødvendig å bruke denne blokka. Nederst på listen står det hvor lang den er: 
 .
.
Blokka si_i_sekunder gir anledning til å velge et antall sekunder teksten skal vises. Den må man bruke når blokka står midt inne i programmet. Hvis blokka si_ står midt inne i programmet, stopper ikke programmet opp for å vise teksten. a blir øyeblikkelig endret med 1 og teksten er borte før man oppdager den. Når blokka si_ er plassert helt til slutt i programmet, blir det stående til programmet kjøres på ny.
Med store tall tar det flere sekunder før alle faktorene er på plass i lista. Ved å slå på turbo reduseres tiden betydelig.
Programmet kan bli modifisert slik at for hver faktor «a» programmet finner, blir to faktorer lagt til i listen: faktoren «a» og «Mitt tall» / «a». Da er det nok å sette antall gjentakelser til større enn kvadratroten av «Mitt tall». Dette grepet reduserer tiden betydelig. Dette kalles optimalisering og spiller en sentral rolle i programmering.
Denne videoen viser tiden programmene kjører med hver av de to metodene med turbo skrudd på.
Utforske
Elevene kan bruke programmet til å bli nærmere kjent med egenskaper til tall. Her er noen forslag til hva elevene kan undersøke:
- Hvilket tall under 100 er delelig med flest tall?
- Er det noen tall som bare gir ett element i lista?
- Er det noen tall som gir ei tom liste? Hva betyr det?
- Hvilket tallet nærmest 1000 gir ei tom liste?
- Hvilket tall under 10000 gir lengst liste?
Modifisere
Elevene kan bli utfordret på å modifisere programmet slik at det også gir tilbakemelding på om tallet er et sammensatt tall eller et primtall.
Utfordringer
Oppgaver knyttet til brøk
Elevene kan bli utfordret på å lage program som
- gjør om en brøk til desimaltall med to desimaler
- gjør om en uekte brøk til blandet tall
- finner minste felles multiplum til to eller flere tall
- finner største felles faktor til eller flere tall
- finner fellesnevner til to eller flere tall
- utfører en eller flere regneoperasjoner med brøker
Collatz' formening
Den tyske matematikeren presenterte i 1937 et tallproblem som til nå – i 2023 – ennå ikke er bevist. Problemet er enkelt å forstå:
- Velg et hvilket som helst naturlig tall (et helt, positivt tall)
- Sjekk om tallet er delelig med 2
- Er tallet delelig med 2: dividerer tallet med 2 slik at du får det et nytt tall
- Er tallet ikke delelig med to: Multipliser tallet med 3 og adder 1. Dette blir nå det nye tallet.
- Gjenta punkt 2 til det nye tallet er 1.
Lag et dataprogram som sjekker om et hvilket som helst tall ender på 1 når man følger punktene 1-3.