Modul 6 - Simulering

Ett kast om gangen

Kaste én mynt

Kron eller mynt? Denne aktiviteten brukes av dommerne i ulike idretter, for eksempel fotball og håndball, for å avgjøre hvilket lag som får velge hvilken banehalvdel de skal ha i første omgang.

La elevene kaste en mynt. For hvert kast noterer de om utfallet blir mynt (M) eller kron (K). Alternativt kan man kaste en vanlig terning og registrere om den viser partall (P) eller oddetall (O). Aktiviteten kan gi oss en forståelse av store talls lov som er et viktig aspekt ved sannsynlighetsbegrepet.

Aktiviteten kan brukes til å undersøke to interessante forhold:

• Hvor mange M-er og K-er har det blitt etter 10 kast, 20, kast osv. opp til 50 kast. Blir det like mange av hver?
• Hvis man ser på rekken av kast, kommer det noen serier med mange K-er eller M-er etter hverandre? Hva er den lengste serien med enten K-er eller M-er?

Tolke program – Kron eller mynt?

Arbeidsark 06a Kron eller Mynt (pdf)

Kommentarer

Programmet på dette arbeidsarket inneholder tre figurer: Abby, Story-K og Story-M.

De tre figurene samhandler gjennom meldinger som Abby sender. Her må man merke seg et viktig prinsipp: De handlingene hver figur skal utføre, må man lage mens den aktuelle figuren er aktivert. Det får man til ved å klikke på figuren under resultatvinduet.

Utforsk

Utforskingen blir mer effektiv om to eller tre arbeider sammen med hver deres oppdrag:

1. Lag programmet sammen i Scratch, kjør programmet og noter resultatene.
2. Hvor stor er forskjellen mellom de to utfallene etter 10 kast, 20 kast, 30 kast osv.?
3. Kom alle parene i klassen til samme resultat? Diskuter.
4. Lag en felles oversikt av klassens resultater og vurder tallene.

Kommentar

Undersøkelsen elevene gjør her kan danne grunnlag for en diskusjon om absolutt forskjell og relativ forskjell. Man kan ta utgangspunkt i noen resultater elevene har kommet fram til, eller benytte disse dataene som ble resultatet av en undersøkelse.

• 10 kast ga 3 K og 7 M. Forskjellen mellom dem er 4.
• 20 kast ga 12 K og 8 M. Forskjellen mellom dem er 4.
• 50 kast ga 27 K og 23 M. Forskjellen mellom dem er 4.

Den absolutte forskjellen er 4 på alle tre undersøkelsene. Den relative forskjellen er 0,4 på 10 kast, 0,2 på 20 kast og 0,08 på 50 kast.

Planlegg program som beregner antall prosent K og M

Passer best for arbeid i par eller mindre grupper. Programmet skal brukes til en utforsking der elevene etter hver utprøving må notere resultatene de får. Før elevene får arbeidsarket: Utfordre gruppene på å lage en hypotese om hva forskjellen mellom de to prosentverdiene vil bli ved henholdsvis 100, 500 og 1000 kast.

Arbeidsark 06b K eller M prosent utforsking (pdf)

Oppsummering

Legg gjerne opp til en samtale når gruppene har skrevet sin hypotese og laget forslag til hva som må legges inn i de åpne rommene. La gruppene få anledning til å dele sine forslag med hverandre slik at alle får mulighet til å lage et program som fungerer på første forsøk.

Kommentarer

Til dette programmet er det ikke nødvendig å bruke figurene Story-K og Story-M. Det er tilstrekkelig med figuren Abbey eller en tilsvarende figur. Merk at variablene «antall kast», «prosent M» og «prosent K» må være synlige slik at elevene får notert data til utforskingen.

Blokka som skal inn under ellers: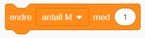

Beregning av prosent K:

Beregning av prosent M:

Dokumentet 06 Oversikt programmer simulering inneholder også programmet 06 K-M? % med liste. Det programmet bruker lister for å holde orden på antall M og K.

Oppsummering etter utforskingen

La elevene presentere resultatet av sin utforsking. Hvis resultatene fra hele klassen blir lagt inn i et regneark er det mulig å beregne en gjennomsnittlig forskjell mellom prosentene for M og K ved ulike antall K. Er elevene enige om hvor mange kast som skal til for at begge prosentene skal ligge mellom 49 og 51?

Hvor mange M-er eller K-er kommer etter hverandre?

07 Kron eller mynt? prosent og streng on Scratch (mit.edu)

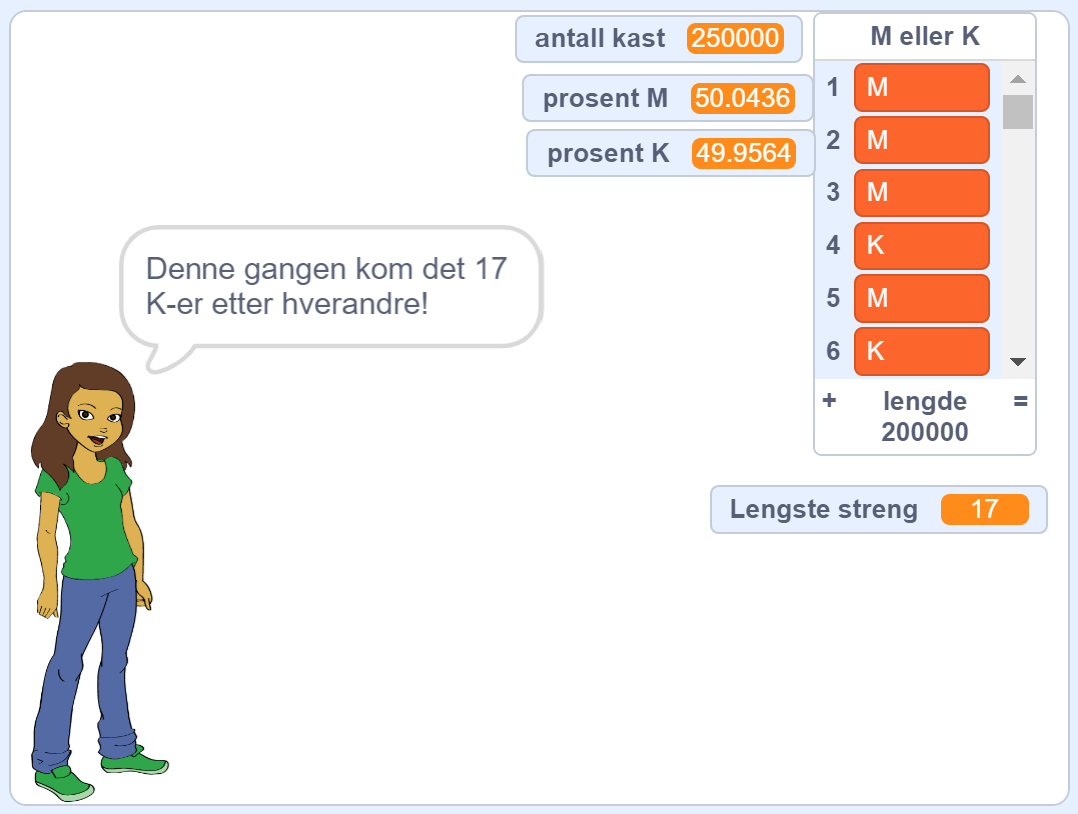
Programmet beregner hvor mange prosent M-er og K-er det blir – og hvor lang den lengste strengen er, dvs. hvor mange like, M-er eller K-er, som kommer etter hverandre.

Prosentverdiene er avrundet til helt tall.

La elevene gjette lengden på strengen om man tar 100 kast. Kjør programmet flere ganger med 100 kast og la elevene notere lengste streng for hver gang.

Gjenta med andre antall kast.

Kommentarer

Maksimum antall elementer i ei liste er 200 000. Det er derfor ikke noe poeng i å kaste flere ganger når man skal finne antall K-er eller M-er etter hverandre. Antall prosent K-er og M-er blir beregnet, men lengste streng gjelder bare for de 200 000 første. Eksemplet viser lengste streng på de 200 000 første av 250 000 kast.

Får jeg en sekser nå?

Hva vet elevene om utfall når man kaster en vanlig sekssidet terning?

Aktuelle spørsmål elevene kan diskutere:

• Er det vanskelig å få en sekser når man kaster en vanlig terning?
• Hvor stor er sjansen for å få en toer?
• Hvis man kaster 60 ganger, hvor mange enere kan man da forvente?

Hvis elevene har liten erfaring med slike spørsmålstillinger, vil det være en fordel å la dem samarbeide to og to om å kaste en terning og notere utfallet for hvert kast. Kaster hvert par 10-15 ganger får klassen en stor datamengde! Lag en frekvenstabell med resultatene fra alle gruppene. Er frekvensen på hver verdi likelig fordelt, eller er det noen verdier som skiller seg ut?

Et dataprogram kan utføre en simulering med mange kast på svært kort tid. Det gir elevene mulighet til å få erfaring med de store talls lov.

Tolke, beskrive og lage program

Arbeidsark 06c terningkast til seks (pdf)

Utforsking

La elevene kjøre programmet flere ganger. For hver gang programmet kjøres må elevene notere antall kast før det kom en sekser. Ta en oppsummering i klassen:

• Hvor mange ganger ble det en sekser på første kast?
• Hvor mange ganger ble det en sekser etter seks kast?
• Hvor mange ganger måtte det mer enn 15 kast til før det kom en sekser?
• Hva er høyeste antall kast før det kom en sekser?

Program som simulerer terningkast til det blir en sekser

Programmet lar deg velge antall testrunder,  lagrer resultatet for hver testrunde i ei liste og gir informasjon om det største antall kast for å få seks.

Simulere terningkast – gjennomsnitt

Resultatvinduet kan for eksempel se slik ut før og etter det blir kjørt.

Oppdrag til elevene

Lag et program

• der brukeren bestemmer antall terningkast programmet utfører
• som summerer verdien til alle kastene
• beregner gjennomsnittet av kastene

Kommentar

Elevene kan utfordres på å lage dette programmet fra bunnen av.

Elever som sliter med å komme i gang kan få arbeidsark 06d til hjelp

Arbeidsark 06d flytskjema gjennomsnitt (pdf)

Noen vil kanskje også ha behov for et påbegynt program som de fullfører:

Arbeidsark 06e terningkast gjennomsnitt (pdf)

Kommentarer

Gjennomsnittet kan beregnes enkelt slik: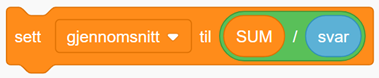

Hvis antall gjentakelser ikke er et «fint tall», kan gjennomsnittet komme med mange desimaler.

Det er mulig å få gjennomsnittet avrundet til to desimaler med dette oppsettet:

Tilbakemeldingen blir da

Utforsking

La elevene kjøre programmet mange ganger med samme antall kast.

For hver gang programmet blir kjørt markerer elevene gjennomsnittet på ei tallinje.

Arbeidsark 06f gjennomsnitt tallinje (pdf)

Oppsummering

Når elevene har samlet nok data med forskjellige antall kast er det tid for en samtale om resultatene. Start gjerne med disse to spørsmålene

• Hva legger dere merke til?
• Er det noe dere lurer på?

Dataene gir anledning til å løfte fram begrepene spredning og «de store talls lov». Jo flere kast, jo mer samlet og nær det teoretiske på 3,5 blir resultatene.

Et dataprogram gjør jobben

Programmet lar brukeren velge et antall kast og beregner gjennomsnittet av kastene. Gjennomsnittet blir markert med et blått punkt i diagrammet. Brukeren må også velge et antall ganger denne simuleringen skal gjennomføres.

Spare resultatene i ei liste

Oppdrag til elevene

Arbeidsark 06g terningkast med liste (pdf)

Utforsking

Hvis klassen samler resultatene fra flere grupper til en felles utforsking, får man et stort tallmateriale å studere. For enkelhets skyld kan det være lurt å velge et antall kast som gjør sammenlikning av utfallene enklere.

Hvis alle starter med 60 kast, vil forventningen være 10 av hver verdi. Får noen grupper frekvens 10 på en eller flere verdier? Hva er det største avviket over/under frekvens 10?

Et eksempel:

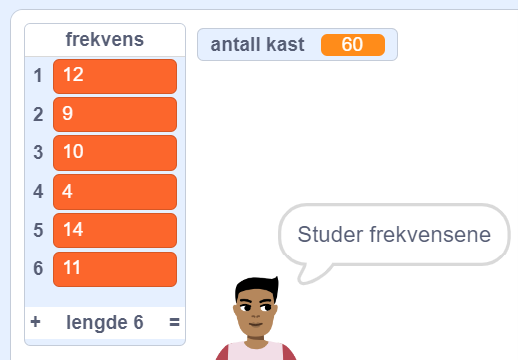
Største avviket fra forventet frekvens er 4.

Fortsett med 600 kast og still samme spørsmål, men nå med 100 som forventet frekvens. Tenker noen elever at avviket nå blir større? Et eksempel:

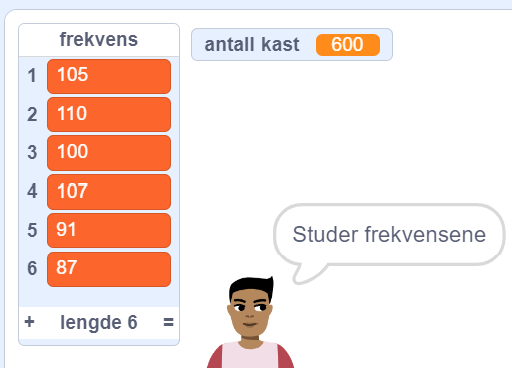
På disse 600 kastene var det største avviket på 13.

Er det et større avvik enn 4 på 60 kast?

Undersøk også med 6000 kast.

Oppdrag til elevene

Arbeidsark 06h SUM to kast med liste (pdf)

Kommentar

Når man kaster to vanlige terninger, kan ikke summen bli 1. I listen med frekvenser vil verdien på 1 alltid være 0:

Når vi tar med 12 elementer i listen, får vi en fin frekvenstabell. Det blir samsvar mellom elementnummer og SUM. Som bildet viser, skjedde det 17 ganger at summen ble 2 på de 600 kastene.

Utforsking

La elevene diskutere hvordan en utforsking med dette programmet kan legges opp når målet er å undersøke

• hvilken verdi som forekommer oftest.
• om antall kast har noen betydning

La par eller mindre elevgrupper lage en hypoteser til de to målene.

Utfordre gjerne elevene på å bli enige om minst et lite og et stort antall kast alle skal gjøre minst én gang. Det kan gjøre oppsummeringen mer interessant.

La elevene utføre utforskingen og gjøre nødvendige notater.

Oppsummering

Noen elever vil kanskje undre seg over at summen aldri blir 1. Det kan bli en fin liten resonneringsutfordring av det!

Lag gjerne en oversikt som viser resultatet for hele klassen på et utvalg antall kast.
La gruppene diskutere hvor mange ganger de må kaste for å være nesten HELT sikker på at 7 har høyest frekvens.

La elevene teste hypotesene sine.

Kommentar

Vi forventer flest summer på 7 når vi kaster to vanlige terninger slik denne simuleringen viser.

10 simuleringer md 100 kast ga disse resultatene:

• 3 ganger med høyest frekvens for 6
• 4 ganger med høyest frekvens for 7
• 3 ganger med høyest frekvens for 8

20 simuleringer med 500 kast ga disse resultatene:

• 16 ganger med høyest frekvens for 7
• 2 ganger med høyest frekvens for 8
• 1 gang lik frekvens på 6 og 7
• 1 gang med lik frekvens på 7 og 8

20 simuleringer med 1000 kast ga disse resultatene:

• 19 ganger med høyest frekvens for 7
• 1 ganger med høyest frekvens for 8

Dette programmet er en utvidet versjon av programmet elevene laget. Det viser resultatene med et linjediagram.

Ekstra utfordringer

Elever som liker en ekstra utfordring kan få prøve seg på disse to utfordringene.

Mange slags terninger

Det fins fysiske terninger med 4, 6, 8, 10, 12 og 20 sider. Dataprogrammet i arbeidsark 06h kan endres slik at terningene får så mange sider man ønsker! Her er det bare å forske i vei.

Hva er vanligste summer å få når man kaster terninger med verdier

• 1-6 og 1-10
• 1-8 og 1-12

Undersøk videre selv. Når dere har fått noe erfaring, kan dere velge to terninger og så prøve å lage hypotese på verdier som får størst frekvens før dere de undersøker hypotesen med dataprogrammet.

Diagrammer – en skikkelig utfordring!

To av programmene som er lagt inn i denne modulen, presenterer resultatet av simuleringen både med ei liste og med et diagram. Elever som liker en ekstra utfordring, kan prøve å utvide et av de programmene de allerede har, slik at programmet også lager et diagram som viser resultatene.