Modul 5 - Input, betingelser og tilbakemeldinger

Mål
Matematikk
- Vurdere strategier for å gjette et hemmelig tall innenfor et gitt intervall.
- Vurdere strategier for å finne sammenhengen mellom tall som blir «matet» inn i en funksjonsmaskin (lineær sammenheng) og resultatet som kommer ut.
Programmering
- Kommunisere med et program gjennom å sende og motta informasjon.
- Få programmet til å gi en betinget tilbakemelding ut fra innspill brukeren kommer med.
- Ta vare på innspill brukeren har gjort.
- Introdusere flytskjema
Oversikt over nye blokker i denne modulen
| Utseende | snakkebobler |  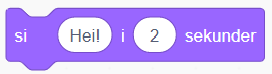 |
| Operator | Sette sammen tekst og variabler |  |
| For å sammenlikne verdier |  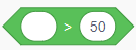  |
|
| Styring | Velge hva som skal skje etter en sammenlikning |  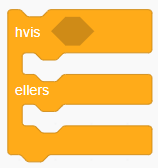 |
| Gjenta til en betingelse er oppfylt |  |
|
| Variabler | Skjul variabel | 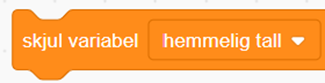 |
| Lage en liste |
Fungerer på samme måte som Lag en variabel. Listen kan for eksempel hete |
|
| Legge elementer inn i en liste | 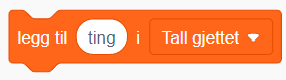 |
|
| Slette alt i en liste |  |
Kort oversikt
Denne modulen handler om å vurdere strategier. I DEL 1 skal elevene finne et hemmelig tall innenfor et oppgitt tall-intervall. De lager først et enkelt program der det hemmelige tallet er i intervallet 1-5 og de får gjette én gang. Programmet utvides slik at det hemmelige tallet er i intervallet 1-64 og man skal gjette helt til man finner det hemmelige tallet. DEL 2 handler om å finne to hemmelige tall etter fem forsøk. Her kan elevene utvikle strategier for å finne konstantene a og b i en lineær sammenheng: ax + b. a og b er de hemmelige tallene som programmet velger og x er det tallet man ber programmet gjøre beregningen med.
Del 1 - Finn tallet
Flytskjema
Hvor mange forsøk trenger du?
Læreren trekker det hemmelige tallet
Læreren har kort med tallene 1-5, trekker tilfeldig ett av dem og legger det på bordet med framsiden ned. Grupper av elever gjetter etter tur på ett av de fem tallene. Læreren skriver tallene fra hver gruppe på tavla. Deretter ser læreren på kortet og gir tilbakemelding på om tallene er feil eller riktig. Det kan være lurt å spare det riktige til slutt.
Introduksjon av flytdiagram
Her møter elevene flytdiagram for første gang. Dokumentet 05 Flytskjema figurer gir en kort beskrivelse av hva hver av de fem figurene brukes til. Elevene kan få utdelt dokumentet sammen med arbeidsark 05a.
Arbeidsark 05a gjett ett forsøk (pdf)
Oppsummering
La noen grupper med litt ulike formuleringer presentere det de har kommet fram til. De andre gruppene kan komme med innspill. Om ingen grupper nevner at de to tomme parallellogrammene i flytskjemaet må inneholde samme tekst som de to blokkene si _ i programmet, kan de bli utfordret på å forklare hvor i programmet man finner de enkelte delene av flytskjemaet.
Kommentarer
I rektanglet kan teksten for eksempel være «velg tilfeldig tall 1-5». I de to parallellogrammene kan teksten være «RETT tall» ved vurdering JA og «FEIL tall» ved NEI. Det vil ikke alltid være slik at til hver figur i flytdiagrammet kan man bruke en enkelt blokk som kan utføre handlingen figuren beskriver. Ofte må man lage en liten kodeblokk for å få utført en det som står i en figur i flytskjemaet. Noen ganger legger man også til blokker som ikke er beskrevet, som for eksempel blokka skjul (hemmelig tall) som skal sikre at det hemmelige tallet ikke blir avslørt for brukeren når programmet blir kjørt.
Tilbakemeldingen til brukeren er betinget av hvilket svar brukeren gir. Blokka hvis ellers gir betingelsen. Den må inneholde en av operatorene =, > eller <. Den valgte operatoren gir betingelsen for hvilket svar brukeren skal få.
Lag programmet og bruk det til en utforsking
Arbeidsark 05b utforsk og notér (pdf)
Oppsummering
Hvis man samler utforskingen fra alle elevene/elevgruppene i klassen, har man et stort tallmateriale man kan undersøke. Dataene kan med fordel samles i et regneark. Forslag til spørmål som kan undersøkes:
- Hvor mange fikk riktig på første gjett?
- Hva var det høyeste antall gjett hver av gruppene måtte bruke.
- Se på alle antall kast for å få 1. Hvor mange kast var det i gjennomsnitt?
Hvor mange kast var det i gjennomsnitt på de andre tallene?
Gjett til du får rett
Programmet skal nå utvides slik at brukeren får tilbakemelding på om tallet brukeren gjetter er for stort eller for lite.
Gjett med tilbakemelding
Læreren skriver et tall fra og med 1 til og med 64 og holder tallet skjult for elevene. Små grupper av elever skal gjette hvilket tall læreren tenker på. Læreren ber elevgruppene skrive tallet de vil gjette på. Gruppe får etter tur si hvilket tall de har skrevet og læreren gir beskjed om tallet er for stort, for lite eller om det er riktig. Elevene bør notere responsen fra de andre gruppene og eventuelt endre tallet gruppen hadde tenkt å foreslå. Når en gruppe gjetter rett tall, er det tid for oppsummering. Oppsummere med en samtale om hvilke strategier gruppene har valgt for å finne det «hemmelige» tallet raskest mulig. Er det en strategi som sikrer at man garantert gjetter rett tall etter et bestemt antall forsøk?
Sammenlikn flytskjema
Arbeidsark 05c flytskjema flere forsøk (pdf)
Oppsummering
Skriv gjerne stikkord om hva som er likt og hva som er forskjellig mens gruppene deler sine tanker og har fått svar på ting de måtte lure på. Det kan være nyttig å utfordre elevene på å foreslå hvilke blokker som kan brukes til de ulike figurene i flytdiagrammet, før de studerer arbeidsark 05c program flere forsøk.
Studer det uferdige programmet
Kodeblokkene A og B er laget ut fra de to flytskjemaene elevene nettopp har sammenliknet.
Arbeidsarket egner seg til en diskusjon i små grupper før en oppsummering i hel klasse.
Arbeidsark 05d program flere forsøk (pdf)
Oppsummering
La gruppene få dele sine tanker om spørsmålene på arbeidsarket. Sørg for å få fram en god begrunnelse for at programmet går helt til man har gjettet riktig svar. Utfordre gjerne elevene på å forklare forskjellen på gjentablokka i dette nye programmet og den gjentablokka de har brukt tidligere.
Kommentar
Det er tre ulike blokker med gjenta: et visst antall ganger, for alltid og til en betingelse er oppfylt. En blokk med betingelse må på samme måte som blokkene med hvis, inneholde en av operatorene =, > eller <.
Elevene lager programmet og bruker det til en utforsking
Elevene prøver programmet noen ganger. For hver gang de gjetter et tall, noterer de hvilket tall de gjettet på og om tallet var for stort eller for lite. De holder på helt til de har gjettet det hemmelige tallet.
Oppsummering
Læreren legger opp til en samtale om ulike strategier elevene kan bruke når de gjetter. Mulige spørsmål å stille:
- Er det mulig å gjette uendelig mange ganger uten noen gang å få rett svar? Hvordan kan det skje?
- Hvorfor er det lurt å notere tallene dere gjetter på, og svarene dere får?
- Hvordan har dere ordnet notatene deres?
- Lisa påstod at hun aldri vill trenge mer enn sju forsøk på å gjette riktig tall. Har hun rett i det?
Kommentarer
Noen elever velger kanskje tilfeldige tall uten noen spesiell strategi enn at neste tall er større eller mindre enn det forrige, alt etter hvilket svar de fikk. Hvis de tillegg har uryddige notater, kan de komme til å gjette på tall som er høyere enn et tall det allerede har notert er for høyt. Mange elever reflekterer lite over gode måter å gjøre notater på. Disse vil ha stor nytte av å bruke tid på spørsmål 3. Få fram og vurder styrke og svakhet med ulike måter å notere på. Spørsmål 4: En god strategi for å sikre seg at man finner det ønskede tallet er først å gjette på det midterste tallet (her 32). Da er halvdelen av tallene ekskludert når vi får vite om tallet er for stort/lite. Neste gjett bør da være 16 eller 48. Nok en gang blir mulige valg halvert. Slik kan vi fortsette, og etter 6 halveringer er det kun ett tall igjen: 32, 16, 8, 4, 2, 1.
Tips: En liten endring som gir mer liv til programmet
Det er mulig å få det hemmelige tallet med i svaret til slutt i programmet. Da legger vi blokka sett sammen inn i si-blokka: 
Vi kan også legge sett sammen-blokka inn i spør-blokka slik at tilbakemeldingene inneholder både svar og om svaret er for stort eller for lite. Tilbakemeldingene kan da bli slik:



Introduksjon av liste
Ei liste kan være nyttig i mange sammenhenger. Programmet kan modifiseres slik at brukeren selv slipper å notere om tallene er for store eller for små. Informasjonen kan bli lagt inn i ei liste etter hvert gjett.
Tolke program
Bruk av lister blir introdusert gjennom tolking av programmet
Arbeidsark 05e 1-n med liste (pdf)
Oppsummering
La gjerne elever som lurer på noe eller er usikre på noe slippe til med sine spørsmål.
Utfordre elevene på å forklare hvordan hver av de tre variablene største tall, hemmelig og tall jeg gjetter endrer verdi underveis når programmet blir kjørt.
Hvordan sikrer programmet at brukeren får tilbakemelding når det blir gjettet riktig tall?
Lage og bruke programmet til en utforsking
Før elevene skal lage programmet, bør de få en innføring i hvordan man lager lister.
Elevene lager programmet og tester at det fungerer, før de bruker programmet til en utforsking og reflekterer over strategier for å finne tallet på færrest mulig forsøk.
Arbeidsark 05f utforsk og noter (pdf)
Oppsummering
Utforskingen gir mulighet for å utfordre elevene på å argumentere både for strategier og største antall gjett. La gjerne elevgrupper få presentere sine argumenter. Når en elevgruppe har presentert sitt argument bør de andre elevene eller gruppene få anledning til å be om en utdyping om det var noe de ikke forstod. De andre gruppene kan bli også bli utfordret på å sammenlikne argumentet som ble presentert med sitt eget argument. Finn likheter og forskjeller mellom argumentene.
Kommentarer
Når man bruker blokka tilfeldig fra _ til _ kan man få alle hele tall fra og med det første til og med det andre tallet man skriver inn.
Til spørsmål 2d
Under oppsummeringen etter programmet der det hemmelige tallet tilhørte intervallet 1-64 ble det argumentert for at største antall gjett er seks. 64 er valgt fordi det er en potens av 2 (64 = 26). Hver gang man halverer kommer man til et nytt tall som kan halveres? Men hvordan blir det med tall mindre enn 64?
Eksempel
Man kan velge tall i intervallet 1-50. Det hemmelige tallet er 27. Brukeren gjetter
- 25 – for lavt
- 37 – for høyt
- 31 – for høyt
- 28 – for høyt
- 26 – for lavt
- 27 – riktig
Strategien i eksemplet er å runde ned når differensen er et oddetall. 50 – 25 = 25. Halvdelen av differensen er 12,5. Avrunding ned gir 12, så neste gjett blir 37 (25+12). Man ender opp med seks forsøk her også. Men hva skjer om man i stedet runder oppnår differensen er et oddetall?
Spørsmål å reflektere over:
- I hvilket intervall er man garantert å få riktig tall på max seks forsøk om man følger strategien om å halvere.
- I hvilket intervall er man garantert å finne riktig tall på max
- fem forsøk
- fire forsøk
Del 2 - Funksjonsmaskin
Finn de to tallene
Funksjonsmaskin
Læreren velger seg et enkelt lineært funksjonsuttrykk. For eksempel y = 2x + 3.
Elevene blir bedt om å gi læreren et tall og læreren sier hva resultatet blir etter at tallet er matet inn i «Funksjonsmaskinen»:
Eksempel: Elevene sier fem og læreren svarer 13. Tallene skrives på tavla.
Prosessen blir gjentatt til det står fem tallpar på tavla.
Elevene studerer tallene som er lagt inn funksjonsmaskinen og hvilke tall som da kom ut. Utfordringen blir å resonnere seg fram til hva funksjonsmaskinen gjør med tallet som blir lagt inn.
Oppstart
En mulig start på programmet Funksjonsmaskin
Arbeidsark 05g oppstart funksjonsmaskin (pdf)
Oppsummering
Spørsmålene 1. og 4. er spesielt egnet til å utfordre elevene på å argumentere for svarene sine. Legg opp til en samtale med begrunnelser for alle spørsmålene.
Kommentar
- Det må være fire gjentakelser. Første svar blir gitt før man startet på blokka gjenta. Deretter får man spørsmålet fire ganger til.


- Etter at det femte tallet er valgt, går programmet ut av løkka og avslutter med å fortelle brukeren resultatet uten å gi mulighet for nytt forsøk.
Lag og test programmet
Etter oppsummeringen bør elevene få anledning til å fullføre programmet eller endre på noe av det de hadde kommet fram til i gruppearbeidet. Elevene bør sjekke om programmet stopper etter at de har valgt tall fem ganger.
Det er mange figurer å velge blant i Scratch. Oppfordre gjerne elevene til å velge en figur som passer til programmet de skal lage. Her er det en funksjonsmaskin man skal gi et tall, og funksjonsmaskinen gir et svar. Da kan figuren Retro Robot være et alternativ:

Planlegg fortsettelse på programmet
Første del av programmet sikrer at brukeren får gjette fem tall og får en tilbakemelding etter hvert gjett. Siste del av programmet skal gi brukeren mulighet for å gjette på de to hemmelige tallene og få tilbakemelding på om tallene er riktige.
Lag en plan for resten av programmet
Arbeidsark 05h flytskjema funksjonsmaskin (pdf)
Oppsummering
Lurer noen elever på hvorfor det står gjenta 5 ganger når starten på programmet som allerede er laget kun gjentar 4 ganger? Om ingen har gode forklaringer er det på sin plass å minne elevene på forskjellen mellom flytdiagram og programmering. Flytdiagrammet forteller hva vi ønsker programmet skal gjøre: Programmet skal velge to tilfeldige tall. Brukeren skal gi input på fem tall og programmet skal gi tilbakemelding uten at brukeren får flere muligheter til å gi input. Hvordan det skal løses i programmeringen, blir en utfordring når man starter programmeringen.
La gjerne gruppene sammenlikne eget flytdiagram med flytdiagrammene til andre grupper. Er det ulike måter å lage programmet på? Gi elevene anledning til å endre sitt flytdiagram de får se en mulig løsning på resten av programmet.
Fra flytskjema til kodeblokk
Før elevene får arbeidsark 05i, kan de få opplyst at den første blokka, si_, erstatter den siste blokka i den delen av programmet de allerede har laget. Resten av blokkene utgjør da siste del av programmet.
Arbeidsark 05i siste del funksjonsmaskin (pdf)
Oppsummering
La gjerne elever som lurer på noe eller er usikre på noe slippe til med sine spørsmål.
Har noen elever en forklaring på hvorfor blokka si _ er byttet ut med si _ i _ sekunder?
Hvordan løser programmet utfordringen med å kontrollere at brukeren har gjettet riktig på begge tallene?
Kommentarer
Merk at den første blokka er en annen enn den siste blokka på begynnelsen av programmet. Blokkene inneholder samme tilbakemelding. Endringen er gjort for å fremheve viktige egenskaper ved de to blokkene si _ og si _ i _ sekunder. Når programmet kommer til blokka si _ går den straks videre i programmet. Det går så raskt at en ikke vil oppdage det en gang. Unntaket er når blokken kommer til slutt i en kodeblokk og programmet ikke går videre før brukeren fortar seg noe. Da blir teksten stående slik man har sett i første del av programmet. Man vil ikke merke noe om den nye blokka si _ i _ sekunder blir lagt til uten å fjerne blokka si _.
Dette programmet benytter også den logiske operatoren og. Her er det to betingelser som må være oppfylt for at programmet skal gi tilbakemelding på at svaret er riktig. Brukeren må oppgi verdiene til a og b og begge må være riktige. I den logiske operatoren og må det ligge to logiske operatorer.
I de åpne feltene på variablene a-gjett og b-gjett skal det stå 
I blokka hvis mangler  . Merk at de to åpne feltene i blokka si_ enten kan ha variablene a og b eller variablene a-gjett og b-gjett. Begge bekrefter at brukeren har gjettet riktig.
. Merk at de to åpne feltene i blokka si_ enten kan ha variablene a og b eller variablene a-gjett og b-gjett. Begge bekrefter at brukeren har gjettet riktig.
Oppsummering
La elevene tenke over om begge de to blokkene si _ i _ sekunder og blokka si _ må være med i programmet og hva forskjellen på dem kan være. Oppfordre dem gjerne til å teste ut programmet bare med blokka si _ når de skal lage og teste programmet.
Lag, test og utforsk
Arbeidsark 05j lag utforsk og noter (pdf)
Kommentarer
Det er mulig å avsløre tallene a og b etter to tilbakemeldinger. Hvis man velger to påfølgende tall, avslører forskjellen mellom tilbakemeldingene verdien til a.
Ellers trenger man en ekstra operasjon for å finne a.
Eksempel
Hvis a = 3 og b = 7
- Input med 2 påfølgende tall
- Input 2 gir tilbakemelding 13
- Input 3 gir tilbakemelding 16
Forskjellen mellom tilbakemeldingene er 3 og a må være 3. b blir da 7, forskjellen mellom 13 og produktet av 2 og 3.
- Input 3 gir tilbakemelding 16
- Input 7 gir tilbakemelding 28
Forskjellen mellom tilbakemeldingene er 12 og mellom i input 3 og 7 er 4.
Da blir a = 12 : 4 = 3
Den enkleste strategien er kanskje å gi input 0 først. Da har vi verdien til b. Om vi da gir input 1 vil a være forskjellen mellom de to tilbakemeldingene.
Oppsummering
Gruppene bør få anledning til samtale om ulike strategier. Elevene kan også bli utfordret på å forklare hvorfor det er tilstrekkelig med input to ganger for å kunne avsløre verdiene til a og b.
Hvis ikke poengene er kommet fram i samtalen kan læreren spørre om
- hva som skjer når vi gir input 0
- man trenger andre strategier hvis a og b også kan være negative
Tilbakemelding i liste
Utvidelse av programmet
Funksjonsmaskinen er laget slik at brukerne selv må notere de fem tallene de velger og svarene de får. Programmet kan utvides slik at brukerne slipper å notere tallene de velger og svarene de får. Da må man lage ei liste tilsvarende den i programmet Gjett tallet. Det kan gjøres på to måter:
- lage to lister: Ei for tallet man velger og ei for svaret man får
- lage ei liste som man f.eks. kaller valgt tall og svar. Verdiene legges inn i listen slik:

Utfordre elevene på å endre programmet slik brukeren slipper å skrive tallene. Valgte tall og svarene må da lagres i en eller to lister.
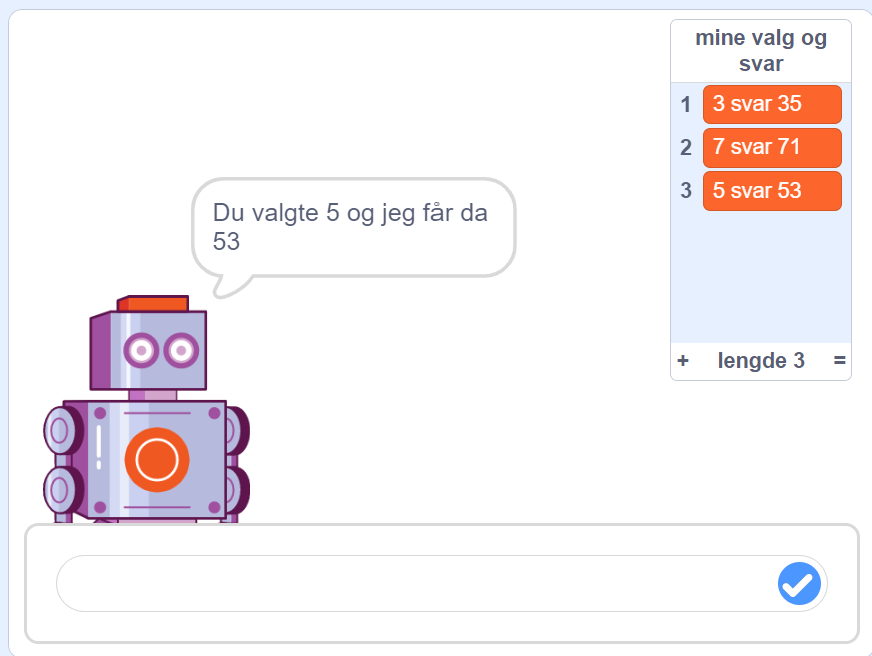
Underveis kan da resultatvinduet se slik ut:
Utfordringer
Elevene kan bli utfordret på å lage program
- som lager regnestykker brukeren må løse
- som løser oppgaver for brukeren
- knyttet til prosentregning
- som gir brukeren de fire første tallene i en tallfølge og ber brukeren finne det femte
- som lager oppgaver med flere alternative svar
- matematikk-quiz