Desimaltall som par av hele tall
Når barn (og voksne) er usikre på meningen med noe, forsøker de å tolke det ukjente inn i en kjent sammenheng. I forbindelse med symboliseringen av desimaltall fører det i noen sammenhenger til at elevene overser desimalkommaet, og i andre sammenhenger til at de tenker at desimaltallet er satt sammen av to uavhengige, naturlige tall som er skilt fra hverandre med et komma.
Denne type tenking gjør at noen elever tolker 5,65 som ”fem hundre og sekstifem”, mens andre kan tolke det som to separate, naturlige tall ”fem og sekstifem”. Ensidig konkretisering av desimaltall ved hjelp av kroner og øre eller meter og centimeter kan være med på underbygge tolkningen av desimaltall som et par av hele tall, der rollen til kommaet er å være skilletegn mellom de to heltallsdelene.

Denne misoppfatningen underbygges av mange i dagligtale:
π ≈ 3,14 (uttales ofte "tre komma fjorten")
1,83 m (uttales ofte "en komma åttitre")
19,90 kr (uttales ofte "nitten nitti")
Det er derfor viktig å referere til plassverdiene i posisjonssystemet i behandlingen av desimaltall. For eksempel bør verdien av `pi` med to desimaler uttales som "tre hele, én tidel og fire hundredeler". Etter hvert som elevene er fortrolig med denne måten å uttale desimaltall på, vil det være naturlig å gå over til en uttale som poengterer delene i desimalene "tre komma en fire". Da blir det tydeligere at det dreier seg om ett tall som består av siffer med verdier, og ikke to tall med komma mellom.
Oppgaver
I prøven misoppfatninger knyttet til tall er det til sammen ni oppgaver som tester om elevene behandler desimaltall som par av hele tall. Nedenfor ser du tre av dem.
Analyse
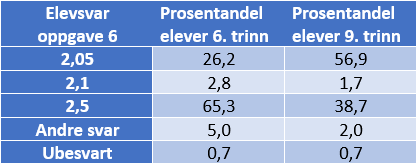
Analyser av oppgave 6 viser at 65 % av elevene på 6. trinn og 39 % av elevene på 9. trinn svarte at 2,5 er halvparten av 4,10. De behandler 4,10 som to sett med hele tall: 4 foran kommaet, og 10 bak kommaet. Mange elever viser at de først halverer 4 og får 2 og så halverer de 10 og får 5. Til slutt setter de sammen de to settene og svarer 2,5. Elevsvarene nedenfor viser eksempler på dette.
Samme tankemåte blir avslørt i oppgave 17, der elevene skal doble 4,6. Over 80 % av elevene (81 % på 6. trinn og 83 % på 9. trinn) som svarte 8,12 i oppgave 17, svarte 2,5 i oppgave 6. Det er derimot betydelig færre elever som svarte at 8,12 er det dobbelte av 4,6, enn de som svarte at halvparten av 4,10 er 2,5. Dette har sammenheng med at elever går inn og ut av misoppfatninger, avhengig av tallene i oppgavene og hvordan elevene behandler tallene.
En annen misoppfatning er at elevene behandler kun heltallsdelen og lar desimaltalldelen stå ubehandlet. Disse elevene svarer at halvparten av 4,10 er 2,10 og at det dobbelte av 4,6 er 8,6. På 6. trinn var det 67 % av elevene som svarte 2,1 i oppgave 6 som svarer 8,6 i oppgave 17.
Elevsvar
Nedenfor er noen elevsvar fra da oppgavene ovenfor ble testet ut på papir, uten svaralternativer. Svarene er gitt av elever fra 5. til 10. trinn.