Andre problemer knyttet til Tall
Tall mellom tallene
En del elever sliter med å forstå at det eksisterer et uendelig antall tall mellom et gitt tallpar. For eksempel vil mange svare at det er to tall mellom 3 og 6, og det er heltallene 4 og 5. Andre vet at det finnes tall med én desimal, og vil telle med tallene fra 3,1 til og med 5,9. De samme elevene vil trolig få vansker hvis de skal skrive et tall mellom 0,5 og 0,6. Årsaken kan være at de ser på desimaltall som par av hele tall.
I noen tilfeller kan misoppfatningen null som plassholder være årsak til samme tenking. Elever i denne misoppfatningen vil for eksempel ikke forstå at 3,05 er et tall mellom 3,0 og 3,1, fordi de oppfatter 3,05 som 3,5. Mer konkretisering gjennom målinger og arbeid på tallinjer kan hjelpe dem ut av misoppfatningen.
Forstå posisjonsprinsippet i desimaltall
En vanlig misoppfatning er at elevene tenker at posisjonene bak kommaet er de samme som foran kommaet (forskyvning). Når disse elevene skal plassere tre siffer bak et komma, vil rekkefølgen på desimalene bli hundredel, tidel og endel. Eksempel: Elevene leser 0,624 som null-komma-sekshundre-og-tjue-fire. De vil si at 6 står på hundredelsplassen (600), 2 står på tidelsplassen (20) og 4 på "enerdelsplassen". En slik lesemåte er med på å forsterke misoppfatningen desimaltall som par av hele tall.

En annen misoppfatning er at plassene bak komma er de samme som foran, bare speilvendt. Nærmest komma er "enerdelsplassen", deretter tidelsplassen ("tierdelsplassen") osv. De vil si at det er 624 hundredeler i stedet for 624 tusendeler i 0,624.
Manglende forståelse av posisjonssystemet blir også avslørt gjennom oppgaver hvor elevene skal skrive brøker (tideler, hundredeler osv.) som desimaltall. De fleste elevene klarer å skrive fem tideler som desimaltall, men får problemer når telleren blir flersifret. Disse elevene mener trolig at når det for eksempel gjelder elleve tusendeler, er det først to nuller bak komma, og deretter kommer verdien til telleren, i dette tilfelle 11 (eller de begynner med å skrive tallet på tusendelplassen). Elevsvar nedenfor viser at elever svarer 0,17 når de skal skrive 17 tideler som desimaltall.
I forbindelse med symboliseringen av desimaltall overser noen elever desimalkommaet, andre ser på kommaet som et skilletegn mellom to heltall. Når elevene skal skrive brøk som desimaltall, tolker noen elever brøkstreken som komma. Eksempel: Fem tideler blir skrevet som 5,10 eller 10,5. Disse elevene bruker komma som skilletegn mellom teller og nevner.
Desimaltall som symbol for del av en hel 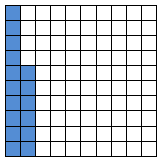
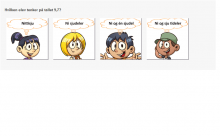
Enkelte elever har problemer med uttrykket «hvor stor del av…». I eksemplet til høyre skal elevene svare med et desimaltall på spørsmålet: «Hvor stor del av hele kvadratet er fargelagt?». Noen elever vil se på seksten små ruter som en bestemt del av hele kvadratet (ett hundre små ruter). For dem vil det være naturlig å svare 16 i stedet for 0,16. Andre vil svare 16,100 fordi de oppfatter desimaltegnet som en brøkstrek eller et divisjonstegn.
Dette blir behandlet grundigere i veiledningen for prøven Brøk og prosent.
Oppgaver
I prøven misoppfatninger knyttet til tall er det sju oppgaver som tester de problemområdene som er beskrevet ovenfor. Fire av disse ser du nedenfor.
Analyse
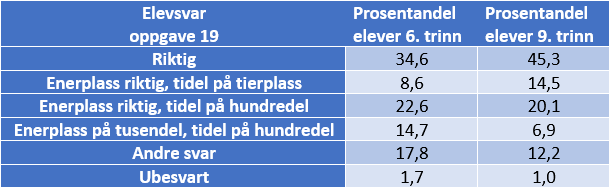
I oppgave 19 skal elevene studere tallet 132,564 og vise om de vet hvor enerplassen og tidelsplassen er. De skal dra riktig plassnavn til riktig rute over eller under sifrene. Tabellen viser at 9 % på 6. trinn og 15 % på 9. trinn plasserer enerplassen riktig og tidelsplassen på tierplassen. Analysene viser at disse elevene har betraktelig lavere gjennomsnittlig dyktighet enn de som svarer riktig på oppgaven. Likevel bør læreren undersøke om feilsvaret skyldes at de ikke har lest oppgaven god nok, eller om det skyldes svak begrepsforståelse for posisjonssystemet.
Det mest vanlige feilsvaret er at tidelsplassen plasseres over hundredelsplassen, altså over sifferet 6 i tallet 132,564. De elevene som gjør dette, men har plassert enerplassen riktig, ser trolig på desimaltallsdelen av tallet som et «speilbilde» av heltallsdelen. Fra komma mot venstre er det enere, tiere, hundrere osv, og fra komma til høyre er det enerdelsplass (endelsplass), tidelsplass, hundredelsplass osv.
Enkelte elever tolker komma som et tusenskille. Disse elevene har plassert enerplassen under tusendelsplassen, under sifferet 4 i tallet 132,564. Tidelsplassen plasserer de over sifferet 6, som egentlig står på hundredelsplassen. Elevene leser tallet som "ett hundre og trettito komma femhundre og seksti fire. Ved å lese tallet slik blir enerplassen "riktig" (fire enere), mens tidelsplassen blir til tierplassen (seks tiere i sekstifire).
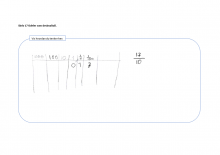
Elevsvarene nedenfor viser at elevene opererer med både enerplass på tusendelsplassen og enerdelsplass på tidelsplassen.
Elevsvar
Nedenfor er noen elevsvar fra da oppgavene ovenfor ble testet ut på papir, uten svaralternativer. Svarene er gitt av elever fra 5. til 10. trinn.