Fjerne og legge til nuller
Mange elever bruker reglene om å fjerne og legge til nuller uten å forstå reglene. Det er naturlig å tenke at dersom en tar bort én eller flere nuller for å gjøre utregningen enklere, må en legge på noen nuller i svaret. Kan en ta bort alle nullene? Hvor mange nuller skal svaret inneholde?
Mange algoritmer og regler i matematikk bygger på mønster og egenskaper i posisjonssystemet. For å kunne bruke disse reglene riktig må elevene forstå hva som skjer med tallene når reglene brukes. Når de ikke har forstått logikken bak reglene, kan det føre til uhensiktsmessig og feil bruk. Reglene kan virke vilkårlige, og de bidrar ikke til tallforståelse knyttet til posisjonssystemet.
I oppgaver med multiplikasjon eller divisjon med tierpotenser (10, 100, 1000 osv.) løser mange elever oppgavene ved å fjerne eller legge til nuller. 
Eksempel på regler:
150 ∙ 30: Ta bort begge nullene, regn ut 15 ∙ 3, sett begge nullene inn i svaret.
150 : 30: Ta bort begge nullene, regn ut 15 : 3, ikke sett noen av nullene inn i svaret.
Elevene bør i stedet for regler få erfaringer med å bruke egenskapene til posisjonssystemet for å løse oppgavene.
Eksempler på utregninger med referanse til posisjonssystemet:
150 ∙ 30 = 15 ∙ 10 ∙ 3 ∙ 10. Det er 45 ∙ 100, som er lik 4500.
150 : 30: Hvor mange ganger går tre tiere opp i 15 tiere?
Oppgaver
I prøven misoppfatninger knyttet til tallregning er det fire oppgaver som tester misoppfatningen fjerne og legge til nuller. Disse oppgavene er med i prøven for både 5.–7. trinn og 8.–10. trinn. Nedenfor ser du tre av dem.
Analyse
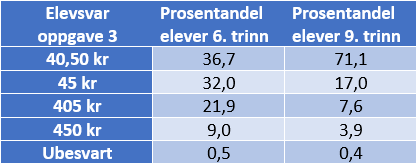
Tabellen viser at 32 % av elevene på 6. trinn og 17 % av elevene på 9. trinn svarer 45 når de skal dividere 4050 med 100. Feilsvaret tyder på at de ser på det å dividere med 100 som å fjerne to nuller, og fjerner de to nullene i 4050, uavhengig av hvilken plass nullene står på. De andre feilsvarene i oppgaven stemmer med at elevene fjerner én av nullene.
I oppgave 10 skal elevene multiplisere 8,4 med 10. De som tenker på multiplikasjon med 10 som å legge til én null, vil svare enten 8,40 eller 80,40. De som svarer 8,40, legger til en null bakerst i tallet, mens de som svarer 80,40, legger en null til både 8 og 4. Elever som svarer 80,40 ser trolig på desimaltall som par av hele tall, som er en misoppfatning som blir grundig testet i prøven Tall.
På 6. trinn svarer 75 % av elevene som svarte 45 kr i oppgave 3, enten 8,4 eller 80,40 i oppgave 10. Tilsvarende tall på 9. trinn er 69 %.
Elevsvar
Nedenfor er noen elevsvar fra da oppgavene ovenfor ble testet ut på papir, uten svaralternativer. Svarene er gitt av elever fra 5. til 10. trinn.





