Didaktisk grunnlag

Silhuett av to hender som holder en puslespillbrikke. Silhuetten er dekket av tall.
Arbeidsmetodikk i og med programmering er nytt for mange matematikklærere. Her beskriver vi noen erfaringer og presenterer PRIMM som arbeidsmetode.

Algoritmisk tenkning har fått en sentral plass i læreplanen for matematikk:

I læreplanen er algoritmisk tenkning synliggjort fordi dette er en viktig problemløsningsstrategi. Når elevene bruker programmering til å utforske og løse problemer, kan det være et godt verktøy for å utvikle matematisk forståelse. (UDIR)

Planlegging av opplegg i programmering er nytt for mange matematikklærere. Etter en kursrekke i programmering for lærere, opplevde vi at to tilbakemeldinger gikk igjen. Disse tilbakemeldingene er også verd å ta med seg når elevene skal lære seg programmering.

Vi vil gjerne ha tips til hvordan vi kan gå fra det analoge til det digitale.

Flott at det ikke er så voldsomt masse oppdrag i løpet av dagen, men at vi får bruke tid på de få ulike oppgavene vi får.

Lærerne så det verdifulle i å veksle mellom analoge og digitale aktiviteter. Den algoritmiske tenkingen kan utvikles gjennom analogt arbeid med pseudokoder, flytskjema og analyse av kodeblokker. PRIMM-metodikken gir gode råd om hvordan det analoge arbeidet kan få en sentral plass i opplæringen, og modulene inneholder mange praktiske eksempler på analoge aktiviteter.

Det tar tid å sette seg inn i måten å tenke på, og lærerne satte stor pris på at de fikk god tid til å diskutere og utveksle ideer, både i mindre grupper og i plenum. Denne måten å bygge opp undervisningen på samsvarer med kjennetegnene på Ambisiøs Matematikkundervisning.

Les mer om ambisiøs matematikkundervisning

Kjennetegn på ambisiøs matematikkundervisning:

  • Elevene arbeider med oppgaver og aktiviteter som fremmer resonnering og problemløsing.
  • Elevene har mange muligheter til å samarbeide, og deltar i matematiske samtaler.
  • Elevene utvikler egne løsningsstrategier.
  • Læreren etablerer et positivt affektivt klassemiljø ved å behandle elevene med respekt, lytte til ideene deres og verdsette dere faglige bidrag.
  • Læreren fremmer dybdelæring og forståelse i matematikk.
  • Lærere kommer med konkrete og konstruktive tilbakemeldinger som utfordrer elevene.
  • Feil anses som en del av læringsprosessen.

Aktivitetene i PRIMM-metodikken utfordrer elevene på resonnering og problemløsing, og passer derfor godt som utgangspunkt for en ambisiøs matematikkundervisning.

Hva er PRIMM?

Mange elever synes det er vanskelig å skrive et program når man starter med et blankt ark. Som lærer kan man bruke varierte teknikker for å hjelpe dem. PRIMM er en forskningsbasert tilnærming til å planlegge opplegg i programmering med fem komponenter:

  • Predict (Forutse)
  • Run (Kjøre)
  • Investigate (Utforske)
  • Modify (Modifisere)
  • Make (Lage)

Forutse

Denne fasen kan er nyttig når elevene skal introduseres for nye begrep. Man gir da elevene et program der de kjenner de fleste kommandoene. Programmet bør bare inneholde ett eller to nye begrep knyttet til programmering. Elevene skal da forklare hva programmet skal utføre og hvilken funksjon de nye begrepene har.

Kjøre

Elevene kjører programmet for å sjekke om det de forutså stemmer. De kan enten selv lage programmet eller kjøre et ferdig laget program. Et ferdig program sikrer at elevene kan fokusere på hva programmet faktisk gjør fremfor å sjekke om de har kopiert korrekt.

Undersøke

Hensikten med den utforskende fasen er å gi elevene mulighet til å utvikle kodeforståelse.

I programmering snakker vi om fire nivåer på kodeforståelse:

  • Atomisk: hele eller deler av en kodelinje
  • Blokk: grupper av sammenhengende kodelinjer
  • Relasjon: kodelinjer som ikke henger sammen, men likevel er relatert til hverandre
  • Makro: oversikt over hele programmer eller større delprogram – avhengig av størrelsen på programmet

Læreren blir anbefalt å bruke fire typer aktiviteter for å gi elevene god anledning til å utvikle denne forståelsen:

  • Spore: elevene ser på variabler i en del av en kode og sporer verdien til variablene gjennom hele programmet. Aktiviteten utfordrer elevene på logisk tenking.
  • Forklare: elevene blir utfordret på å forklare et program på hvert av de fire nivåene i kodeforståelse.
  • Kommentere: Elevene får et program. Til hver linje eller blokk i programmet skriver de en kommentar som forteller hva linjen eller blokken gjør.
  • Feilsøking: Elevene får et program som de skal undersøke nøye. Programmet kan inneholde en feil eller unødvendige koder.

Modifisere

Elevene får et program som skal endres slik at det utfører en annen tilsvarende oppgave, eller noe som tilfører mer til programmet.

Eksempel:

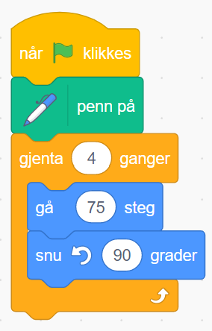
Programsnutt fra Scratch

Programmet tegner et kvadrat. En oppgave kan være å modifisere programmet slik at brukeren bestemmer

  • plassering og orientering til kvadratet
  • hvor mange steg sidelengden skal være

Lage

Elevene lager et helt nytt program fra «bunnen av» der de kan bruke hele eller deler av program de har laget tidligere. Programmet skal ha en ny funksjon eller være knyttet til et nytt problem som skal løses.

Anbefalt arbeidsmetodikk når elevene har en ide til noe de kan programmere:

Analoge aktiviteter

  1. Lag en skisse – hvis det dreier seg om en geometrisk figur – eller kort beskrivelse av hva programmet skal gjøre.
  2. Lag en algoritme, for eksempel et flytskjema, som beskriver hvordan du kan bygge opp programmet.
  3. Hvis programmet er omfattende; identifiser deler av programmet som kan betraktes som en egen enhet som står i relasjon til andre deler av programmet.

Digital aktivitet

  1. Start programmeringen. Kontroller hyppig om programmet gjør det du har tenkt det skal gjøre. Ikke fortsett uten at du har kontroll.

 

 

Kilder

Digital Scotland. What is PRIMM? Lastet fra https://primmportal.com 19. Mai 2022

Fojcik M. K., og Refvik, K. A. S.; Programmeringsstrategier i matematikk. Presentasjon fra verksted på Novemberkonferansen 2021.

Matematikksenteret: Mestre Ambisiøs Matematikkundervisning. Lastet fra matematikksenteret.no 10. juni 2022.

UDIR. Hva er nytt i matematikk? Lastet fra udir.no 1. juni 2022.